纠错编码中的代数理论与方法

屈龙江，　海　昕，　李　超

(国防科学技术大学理学院，湖南长沙410073)



纠错编码中的代数理论与方法

屈龙江，海昕，李超

(国防科学技术大学理学院，湖南长沙410073)

[摘要]纠错编码是保证通信可靠性的重要手段.本文首先介绍了纠错编码的基本概念和主要数学问题，然后基于线性代数、抽象代数的理论与方法，讨论了两类常见的纠错编码——线性码、循环码.

[关键词]纠错编码； 线性代数； 抽象代数； 线性码； 循环码

1问题引入

当今社会，信息无处不在，且已高度数字化. 各种类型的信息，包括文字、图片、音频、视频等，往往按照一定的编码格式编成二进制比特串，然后送上信道传输. 信道也具有多种表现形式，如电话线、网络光纤、大气层(借助于它，嫦娥号才能传回月球表面图片)等. 由于信道质量问题，信息有时会发生错误. 如果发送端不对信息进行任何处理的话，那么接收端接收到信息后就不知道信息是否出错，以及哪位出错. 为了解决这个问题，需要在信息中加入冗余. 让我们先看一个简单例子.

例1电话的噪音很大时，常常把讲话重复几遍. 现在把每个信息0=(00)，1=(10)，2=(01)，3=(11)重复三遍，即变为

0=(000000)，1=(101010)，2=(010101)，3=(111111).

注意到上述4个信息向量中任两个至少有3位不同. 若码字x只有1位出错变成y，则y与x只有1位不同，而y与其他信息向量至少有2位不同，于是可将y“就近”译成x，从而纠正该位错误. 因此，该编码方法可检测2位错误，并可纠正1位错误. 但需要说明的是，冗余的增加使得通信效率降低了，用6维向量传递2位信息，效率减为原来的1/3.

从上例可看出纠错编码的本质. 为了使通信系统具有纠错能力，需要在编码中加入冗余，而这往往以牺牲效率为代价. 如何在效率降低最少的条件下，获得最大的纠错能力，就成了纠错编码理论中一个最基本的问题. 要圆满解决它，数学手段当仁不让.

经历了半个多世纪的发展，纠错编码理论已成为应用数学的一个重要分支，代数、几何、组合等数学理论与方法日渐渗透其中，取得了非常丰富的成果[1-3]. 尽管如此，许多工科研究生对纠错编码往往缺乏了解，即便对一些修过纠错码课程的学生来说，其中蕴涵的数学理论，尤其是代数理论与方法也是浅尝辄止，未曾掌握.

本文将对纠错编码中的代数理论与方法做一简单梳理，目的是向读者展示这一优美的数学理论，同时深化读者对代数学工具的理解. 在这里，我们假定读者已经学习了“线性代数”理论和“抽象代数”理论. 否则，请参考文献[4]，[5].

本文结构如下：第2节介绍纠错码的基本概念和主要数学问题；第3，4节分别介绍线性码和循环码，基于的主要代数理论分别是线性代数和抽象代数；第5节是结束语.

2纠错码的基本概念和主要数学问题

设α=(a1，…，an)∈，则wt(α)=#{i|ai≠0}为α的Hamming重量. 由此定义C的最小距离为

证设发方发送x∈C，由于信道干扰，收方收到y=x+ε，其中ε≠0.

图1

d≤d(x，x′)≤d(x，y)+d(x′，y)，

由三角不等式有

这表明与y距离最小的码字x即为正确码字.

定理2.1说明一个纠错码的最小距离衡量了它的纠错能力.

纠错码的主要数学问题：

(i) 构造好码，即构造码率尽可能高、最小距离尽可能大的纠错码.

(ii) 寻找好的译码算法. 一个码要想在实际中取得良好应用，必须有好的译码方法.

在给定码长n和最小距离d的情况下，问题(i)就是要寻找尽可能多的码字，以便其中两个不同码字之间的最小距离≥d. 这是一个组合数学问题. 下面有两个界.

定理2.2(Hamming界)设C为q元(n，M，d)码，则

定义2.3若码C使得Hamming界成立，则C称为完全码(perfect code).

定理2.4(Singleton界)设C为q元(n，M，d)码，则M≤qn-(d-1).

定义2.5达到Singleton界的码称为极大距离可分码(maximal distance separable code，简称MDS码).

下面将用代数理论刻画、构造完全码与MDS码.

3线性码

线性码是最重要、最基本的一类纠错码，其研究成果也最为丰富，主要原因是可用线性代数理论研究它.

对于线性码，它的最小距离有一个更简单的刻画.

定义3.3设C为一个q元[n，k]线性码. C的生成矩阵G是以C的一组基为行向量所构成的k×n矩阵，即

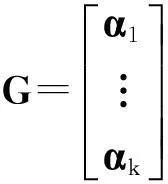
其中α1，…，αk为C的一组q-基.

对于线性码C来说，只要生成矩阵确定了，它的全部码字也就知道了. 事实上，C中任意向量c均可表示为c=(x1，…，xk)G，其中(x1，…，xk)∈.

C的对偶空间称为C的对偶码，记为C⊥，即

C⊥={x∈，∀c∈C}.

C⊥的一个生成阵H称为C的一个校验阵，即对任意c∈C，总有H·cT=0. 事实上，容易证明对任意x∈，x∈C当且仅当H·xT=0. 这也是校验矩阵得名的由来.

生成矩阵和校验矩阵既是线性码的简洁表示，反映其全部性质，也是研究线性码的有力工具，可以给出其性质的更多刻画. 下面是关于最小距离的一个例子.

定理3.4设C为q元[n，k]线性码，H为C的一个校验阵，则C的最小距离为d当且仅当H中任意d-1列线性无关，且存在d列线性相关.

对于线性码，Singleton界变为k≤n-(d-1)，此时MDS码有如下刻画.

定理3.5设C为q元[n，k]线性码，则下列四个条件等价：

(i)C为MDS码，即d=n-k+1.

(ii)C的生成阵G中任意k列线性无关.

(iii) C⊥为MDS码，即C⊥为[n，n-k，k+1]线性码.

(iv) C的校验阵H中任意n-k列线性无关.

证(i) ⟹ (iv).由定理3.4可得.

(iv) ⟹ (i).显然d≥n-k+1，再由Singleton界d≤n-k+1知恰有d=n-k+1.

(i) ⟺ (ii).设

其中αi∈若C不是MDS码，即d≤n-k，则由最小距离定义知C中非零码字c=(c1，…，cn)至少有k位为零. 不妨设c1=…=ck=0，则有0≠a=(a1，…，ak)∈，使得

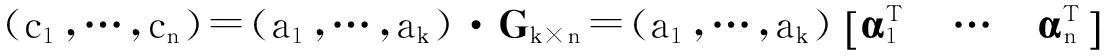
从而

即齐次方程组

考虑到H又是C⊥的生成阵，结合(i)，(ii)等价知(iii)，(iv)也等价.

下面介绍利用多项式理论构造的一类重要线性码.

定理3.6(多项式码)设a1，a2，…，an是中n个不同元素，k≤n≤q，定义

C={cf=(f(a1)，f(a2)，…，f(an))|f∈q[x]，degf≤k-1}，

则C为一个q元[n，k，n-k+1]的MDS码.

证显然C为一个q元n长线性码. 由于次数≤k-1的非零多项式至多有k-1个零点，故cf=cg当且仅当f=g，即证C为[n，k]线性码. 再设0≠cf∈C，则wt(cf)≥n-k+1，即d≥n-k+1. 另一方面，由Singleton界d≤n-k+1，即证C为MDS码.

本节的最后介绍一类重要的完全码——Hamming码. 为此，先引入一些概念. 设α，β为{0}中的任意两个向量，定义α，β等价当且仅当存在λ∈，使得α=λβ，那么{0}中向量恰好可分成个等价类. 在每个等价类中任取一个代表元，作为列向量，构造一个m×n矩阵H，再以H为校验矩阵构造一个线性码C，称之为Hamming码.

定理3.7设C为如上定义的Hamming码，则它是参数为

的q元完全码.

证显然

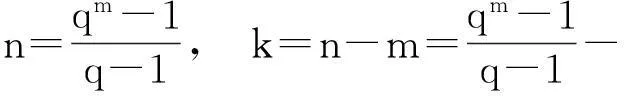
由H的构造方法易知它的任意2列是线性无关的. 而H中存在3列线性相关，因此d=3.

又由于

故C为完全码.

4循环码

循环码是最重要的一类线性码，编、译码的硬件实现十分便捷. 已知的大多数好的纠错码都是循环码.

定义4.1设C为一个q元n长的线性码，若对任意c=(c0，c1，…，cn-1)∈C，总有

(cn-1，c0，c1，…，cn-2)∈C，

则称C为循环码.

本文中均假定(n，q)=1，这是因为好的纠错码大都属于此种情形. 此时循环码也可视为一个理想. 因此，对它的研究不仅可使用线性代数理论工具，更需要抽象代数的理论与方法. 这正是循环码的研究结果特别丰富、构造的好码的数量尤为可观的根本原因.

定义如下映射

φ:=q[x]/(xn-1)，

定理4.2设C为一个q元n长的线性码，则C为循环码当且仅当φ(C)为中的理想.

degg=n-k，

其中k=dimC，C=(g(x))={a(x)g(x)|a(x)∈q[x]，dega

循环码具有多种描述方式. 如上所述，我们可用其生成式或校验式来刻画，即对任意c∈，有

c∈C ⟺ c(x)h(x)=0 ⟺ g(x)|c(x).

另一方面，设

为其在分裂域中的分解，则由g(x)|xn-1与(n，q)=1知α1，…，αn-k为不同的n阶单位根. 进一步

c∈C⟺g(x)|c(x)⟺c(αi)=0，1≤i≤n-k.

于是，也称C是以α1，…，αn-k为根的循环码. 这表明循环码也可用它的根来表示. 利用该表示，我们可以就给出著名的BCH码.

叫做设计距离为δ的BCH码. 若n=qm-1，即，则此时的BCH码也称为本原BCH码.

定理4.4设C为如上定义的BCH码，则C的最小距离d≥设计距离δ.

即

记H=[β(i+l)j]0≤i≤δ-2，0≤j≤n-1为上述齐次线性方程组的系数矩阵，则H可视为C在扩域中的一个校验阵. 取H的任意δ-1列，不妨设为i1，i2，…，iδ-1列，考虑对应的δ-1阶子式

由于βi1，βi2，…，βiδ-1两两不同且均不为零，而上式右边的Vandermonde行列式也不为零，从而H的任意δ-1列线性无关. 由定理3. 4可知d≥δ.

m1(x)=(x-β)(x-β2)(x-β4)(x-β8)(x-β16)，

则β3，β5，β7的极小多项式分别为

m3(x)=(x-β3)(x-β6)(x-β12)(x-β24)(x-β17)，

m5(x)=(x-β5)(x-β10)(x-β20)(x-β9)(x-β18)=m9(x)，

m7(x)=(x-β7)(x-β14)(x-β28)(x-β25)(x-β19).

令g(x)=m1(x)m3(x)m5(x)m7(x)，则C=(g(x))为一个本原BCH码，且其设计距离为9. 由m9(x)=m5(x)知，C的最小距离≥11.

上例表明BCH界不紧. 给出BCH码最小距离的精确公式或更好的下界是一个很重要也很难的数学问题.

相较一般线性码，BCH码的代数结构更好，所以它具有更高效的译码算法，比如广为熟悉的B-M综合算法[1]. 另一方面，BCH码还能设计出任意大的最小距离，因此BCH码在实际中得到了广泛应用，特别是下面的一个子类.

定义4.6设α是q的一个本原元，n=q-1，2≤d≤n，以α，α2，…αd-1为根的q元n-1长的BCH码叫做Reed-Solomon码(RS码)，即

显然RS码C的生成式为

从而C的维数k=n-d+1. 由BCH界知C的最小距离≥d，结合Singleton界知C的最小距离恰为d，即证RS码为MDS码.

RS码事实上是定理3. 6中多项式码的子类. 为说明这一点，设={1，α，α2，…，αq-2}，定义如下一类多项式码

C′={cf=(f(1)，f(α)，f(α2)，…，f(αq-2))|f∈q[x]，degf≤k-1=n-d}.

5结束语

从前文可以看出，在线性码和循环码研究中，线性代数和抽象代数理论与方法起到了十分重要而深刻的作用. 事实上，上述内容已有几十年的历史，属于经典纠错码的范畴. 现代纠错编码理论更加丰富多彩，涌现了代数几何码、有限环上编码、网络编码、量子纠错码、空时码等富有活力的新分支，而对这些内容的研究用到了更多、更深刻、更现代的代数理论. 比如代数几何码以代数几何、代数曲线理论为基本研究工具，有限环上编码以有限环论为基本研究工具，量子纠错码的基本研究工具是复向量空间，空时码的研究用到了丰富而深刻的群表示理论等等. 综上，纠错编码中的代数理论与方法研究丰富多彩、魅力迷人，无论从理论上还是在实践中都有重要的意义. 我们希望更多的青年才俊投身该领域的研究之中.

[参考文献]

[1]冯克勤. 纠错码的代数理论[M]. 北京：清华大学出版社，2005.

[2]MacWilliamsFJ，SloaneNJA.TheTheoryofError-CorrectingCodes[M].Amsterdam:North-HollandPublishingCompany， 1977.

[3]VanLintJH.IntroductiontoCodingTheory[M]. 3thed.Berlin:Springer-Verlag， 2000.

[4]冯良贵，戴清平，李超，谢端强. 线性代数与解析几何[M]. 北京：科学出版社，2008.

[5]李超，谢端强，冯良贵，戴清平. 代数学基础[M]. 长沙：国防科技大学出版社，2000.

AlgebraicTheoryandMethodsofError-CorrectingCode

QU Long-jiang，HAI Xin，LI Chao

(CollegeofScience，NationalUniversityofDefenseTechnology，Changsha，Hunan410073，China)

Abstract:Error-correctingcodeisanimportantmeansofensuringthereliabilityofcommunication.ThefundamentalconceptionsandprimarymathematicalproblemsofError-correctingcodeareinitiallypresented.Thenbasedonthetheoryandmethodsoflinearalgebraandabstractalgebra,twotypesofthefamiliarerror-correctingcode,linearcodeandcycliccode,arefurtherdiscussed.

Keywords:error-correctingcode;linearalgebra;abstractalgebra;linearcode;cycliccode

[中图分类号]O29

[文献标识码]A

[文章编号]1672-1454(2015)01-0007-07