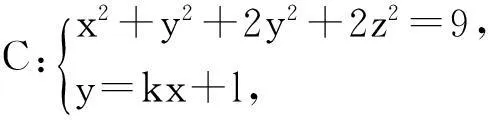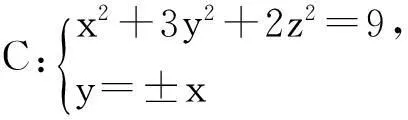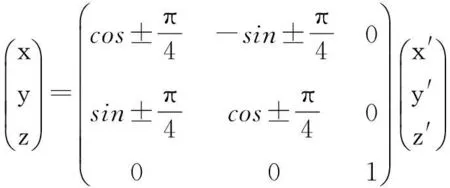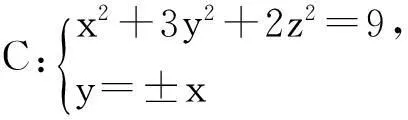新论与二次曲面有交线圆的平面的存在性
金 晶
(1.华中师范大学数学与统计学院,湖北武汉430079; 2. 汉口学院公共数学部,湖北武汉430212)
新论与二次曲面有交线圆的平面的存在性
金晶1,2
(1.华中师范大学数学与统计学院,湖北武汉430079;2. 汉口学院公共数学部,湖北武汉430212)
[摘要]利用平面与球面的任何交线均为圆这一特点,本文研究了与椭球面、双曲面、抛物面交线为圆的平面的存在性问题,提出了不同于旋转变换法和二次型方法的新的更简捷的证明方法.
[关键词]二次曲面; 交线; 圆
1引言
一般地, 平面与二次曲面相交于二次曲线[1], 这种交线能否为圆, 依赖于平面与二次曲面的相对位置关系,那么交线为圆的平面存在么? [2]利用三维空间中的旋转变换,化空间曲线为平面曲线进而讨论曲线何时为圆,从而提出了交线为圆的平面的条件,证明了对于椭球面,双曲面,椭圆抛物面都存在交线为圆的平面,后来,[3,4]利用二次型及特征根理论简化了[2]的证明. 事实上,任何平面和球面交线必为圆,基于这一基本事实,我们进一步简化了[2]的证明过程.
2主要结论
证首先不失是一般性,可设椭球面等同于
Ax2+By2+Cz2=D,0
先将椭球面方程改写为Ax2+(C-B)z2+By2+Bz2=D,再取平面z=kx+l去截椭球面所得曲线为

(1)
将(1)2代入(1)1得
[A+(C-B)k2]x2+By2+Bz2+2k(C-B)xl+(C-B)l2=D,
只要此方程是球面方程,则平面z=kx+l与它的交线C一定是圆. 最简单的方法是取

注1若A=B=C,则本身就是球了,只需取平面z=0. 若A=B≠C,只需取平面z=0.
证首先不失是一般性可设双面等同于
Ax2+By2-Cz2=D,0
先将椭球面方程改写为Ax2+Ay2+(B-A)y2-Cz2=D,取平面去截双曲面所得曲线为

(2)
将(2)2代入(2)1得
Ax2+Ay2+[(B-A)k2-C]z2+2(B-A)klz+(B-A)l2=D,
只要此方程是球面方程,则平面y=kz+l与它的交线一定是圆,若D>0,只需取
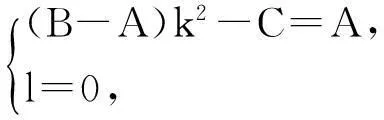
若D<0,则仍需(B-A)k2-C=A,此时可配方如下

注2若A=B,只需取平面z=0.
推论1对于二次锥面,即D=0,交线为圆的平面存在.
证首先不失一般性可设双面等同于
Ax2+By2=2z,0 先将椭圆抛物面方程改写为Ax2+Ay2+(B-A)y2=2z,取平面y=kz+l与椭圆抛物面的交线为 (3) 将(3)2代入(3)1得 Ax2+Ay2+(B-A)k2z2+2(B-A)klz+(B-A)l2=2z, 只要此方程是球面方程,则平面y=kz+l与它的交线一定是圆,只需取 注3若A=B,只需取平面为z=0. 3应用 例1求与椭球面x2+3y2+2z2=9交线为圆的平面. 解首先将椭球面改写为方程x2+2y2+2z2+y2=9,取平面y=kx+l去截椭球面所得曲线为 (4) 将(4)2代入(4)1得(k2+1)x2+2y2+2z2+2kxl+l2=9,为了使上述方程表示某一球面,只需令k2=1,l=0,即所求平面为y=±x. 注4为了验证例1结论的正确性,下面用坐标变换下证明曲线 是圆. 证首先构造旋转变化 (5) 在此变换下,坐标系O-xyz中的平面y=±x化为新坐标系O-x′y′z′中坐标平面y′=0从而交线 由坐标系O-xyz中的空间曲线转化为新坐标系O-x′y′z′中坐标平面y′=0上的平面曲线.在新坐标系O-x′y′z′中曲线C化为 [参考文献] [1]樊恽,刘宏伟. 线性代数与解析几何教程[M].北京:科学出版社,2009. [2]马淑云,刘长保. 与二次曲面有交线圆的平面的存在性[J]. 南都学坛, 2001,(3):19-26. [3]马淑云.再论与二次曲面有交线圆的平面[J]. 南阳师范学院学报(自然科学版),2003,(9):1-6. [4]周华生. 用特征根求二次曲面圆截面方程[J]. 大学数学, 2004, (20):109-112. New Theory on the Existence of Plane Which Intersects with Quadric Surfaces in a Circle JINGJin1,2 (1. College of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China; 2. Mathematics Department of Public, Hankou University, Wuhan 430212, China) Abstract:Using the characteristic that plane intersects with sphere in a circle, this article studied the existence of plane which intersects with ellipsoid, hyperboloid, parabolic surfaces in a circle. Especially, we introduce an easier method to prove this existence result. Key words:quadric surfaces ; intersection line ; circle [收稿日期]2014-11-12 [中图分类号]O182.2 [文献标识码]C [文章编号]1672-1454(2015)01-0110-03