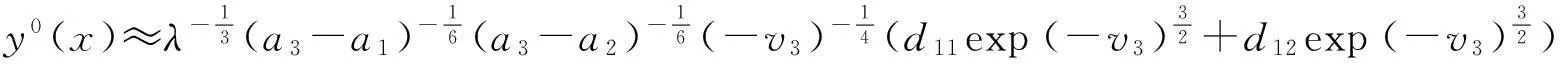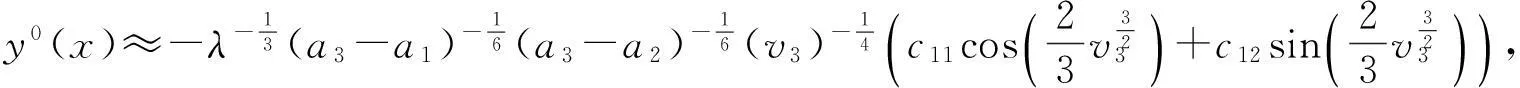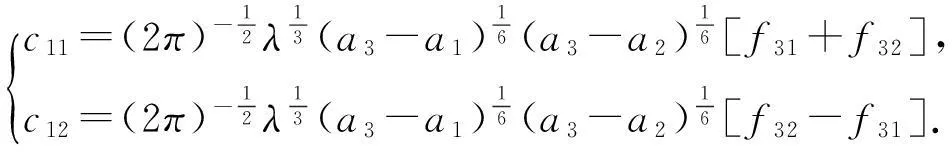A Class of Singularly Perturbed Equations for Larger Parameter with Three Turning Points
-,
(1.Anhui Technical College of Mechanical and Electrical Engineering,Wuhu Anhui 241002,China;
2.Department of Mathematics, Anhui Normal University, Wuhu Anhui, 241000,China)
A Class of Singularly Perturbed Equations for Larger Parameter with Three Turning Points
SHIJuan-rong1,2,YOUYou1
(1.Anhui Technical College of Mechanical and Electrical Engineering,Wuhu Anhui 241002,China;
2.Department of Mathematics, Anhui Normal University, Wuhu Anhui, 241000,China)
Abstract:A class of singularly perturbed problem for larger parameter with three turning point is considered. Firstly, the outer solution in different areasis obtained using the Liouville-Green transform. Then, introducing stretching transform and using the Bessel function of 1/3 and -1/3 order the interior layer solution near thex=a1,x=a2andx=a3is constructed respectively. Finally, the arbitrary constants is selected for the outer solution and interior layer solution using the matching principle.
Key words:turning point; Liouville-Green transform; Bessel function
CLC Number:O175.14Document Code:AArticle ID:1672-1454(2015)01-0001-06
Received date:2014-08-20
Foundation item:Natural Science Foundation of China(11202106)
1Introduction
In recent years, turning point problem of singular perturbation problems become the hot focus. Many scholars have studied the turning point problem of different types using different methods[1-6]. Such as Mo Jiaqi, Ouyang Cheng and so on[7-8]using the Liouville-Green transform and matching principle is studied for a class of two turning points of singularly perturbed problems with large parameters. In this paper, on the basis of a class of three turning points of singularly perturbed equation with big parameters
y″+[λ2(x-a1)(x-a2)(x-a3)+f(x)]y=0,x∈,
(1)
whereλ≫1isadimensionlessparameter,a1,a2anda3arearbitraryconstants,anda1 2Outer solution For simplicity, first on the g(x)=(x-a1)(x-a2)(x-a3), then from Eq. (1), lead into Liouville-Green transform, i.e. let z=φ(x),v(z)=ψ(x)y(x), (2) where functions φ(x) and ψ(x) determine by below. Substituting Eq.(2) into Eq. (1),we have (3) (4) Let (5) thus Eq. (4) is expressed by (6) (7) (8) and Eq. (6) is (9) (10) where c1,c2,d1and d2are arbitrary constants. 3Constructing interior layer solution near x=aj(j=1,2,3) x=ξλ-ω+aj, (12) where ω>0,which is decided below.Substituting Eq. (17) into Eq, (1), we obtain (13) (14) (15) thus the general solution of Eq. (20) denotes by Bessel function of 1/3 and -1/3 order then we can obtain interior layer solution of equation (1) near x=a1: (16) where f11and f12are arbitrary constants. Similarly, we can obtain interior layer solution of equation (1) near x=a2: (17) where f21and f22are arbitrary constants,and Similarly, we can obtain interior layer solution of equation (1) near x=a3: (18) 4Matching the interior and outer solutions 4.1.1a1 The principal term of outer asymptotic solution of Eq. (1) is fixed v1,and let λ→+∞ ,we can obtain v1>0, thus thus (19) where v1→+∞, using by the behavior of Bessel function, we can have (20) using by matching principle, and from Eqs. (19) and (20), we obtain (21) 4.1.2x The principal term of outer asymptotic solution of Eq. (1) is thus (22) where v1→-∞, using by the behavior of Bessel function, we can have (23) using by matching principle, and from Eqs. (22) and (23), we obtain (24) 4.2.1a1 The principal term of outer asymptotic solution of Eq. (1) is thus (25) wherev1→+∞, using by the behavior of Bessel function, we can have (26) using by matching principle, and from Eqs. (25) and (26), we obtain (27) 4.2.2a2 The principal term of outer asymptotic solution of Eq. (1) is thus (28) where v2→-∞,usingbythebehaviorofBesselfunction,wecanhave (29) usingbymatchingprinciple,andfromEqs. (28)and(29),weobtain (30) 4.3.1a2 TheprincipaltermofouterasymptoticsolutionofEq. (1)is thus (31) wherev3→-∞, using by the behavior of Bessel function, we can have (32) using by matching principle, and from Eqs. (31) and (32), we obtain (33) 4.3.2x>a3 TheprincipaltermofouterasymptoticsolutionofEq. (1)is thus (34) wherev3→+∞, using by the behavior of Bessel function, we can have (35) using by matching principle, and from Eqs. (31) and (32), we obtain (36) 5Themainresults Fromtheabove,wehavethefollowingtheorem: TheoremThelargeparametersingularlyperturbedequation(1)withthreeturningpointpossessesouterasymptoticsolution(11a)-(11d)andinteriorlayersolution(16)-(18).Andtheexternalsolutionandtheinnersolutionofarbitraryconstantssatisfythematchingconditions(21), (24), (27), (30) ,(33)and(36),wheref11,f12,f21,f22,f31andf32arearbitraryconstants. Asimilarapproachcanbeused,solvingwithnturningpointproblem. [References] [1]NayfehAH.Introductiontoperturbationtechniques[M].NewYork:JohnWiley&Sons, 1981. [2]MoJiaqi,WangHui.TheshocksolutionforquasilinearsingularlyperturbedRobinproblem[J].ProgressinNaturalScience, 2002, 12(12): 945-947. [3]MoJiaqi,ZhuJiang,WangHui.Asymptoticbehavioroftheshocksolutionforaclassofnonlinearequations[J].ProgressinNaturalScience, 2003, 13(10): 768-770. [4]刘树德,鲁世平,姚静荪,等. 奇摄动边界层和内层理论[M]. 北京:科学出版社, 2013. [5]莫嘉琪. 具有二阶转向点的大参数奇摄动方程[J]. 厦门大学学报, 2005, 44(6):753-755. [6]欧阳成. 一个带m阶转向点的奇摄动特征值问题[J]. 工程数学学报, 2005, 22(3): 559-562. [7]莫嘉琪. 一类具有二个转向点的大参数奇摄动方程[J]. 系统科学与数学,2007,27(5):684-690. [8]欧阳成, 韩祥临. 一具有两个转向点的大参数奇摄动方程的渐近解[J]. 系统科学与数学, 2011, 31(1): 41-47.






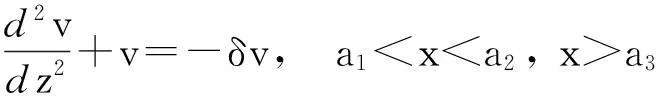

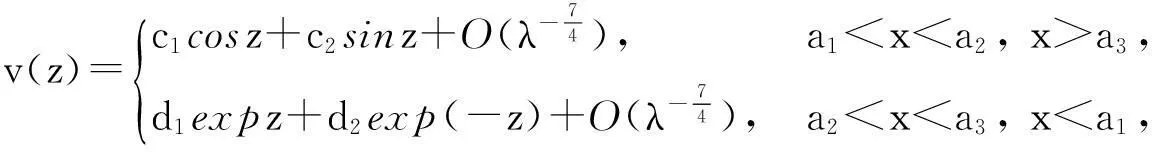


3.1 j=1

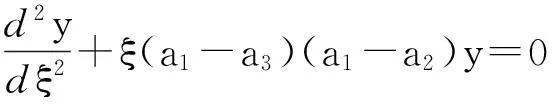




3.2 j=2

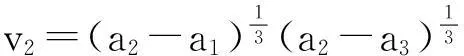
3.3 j=3


4.1 Matching near x=a1









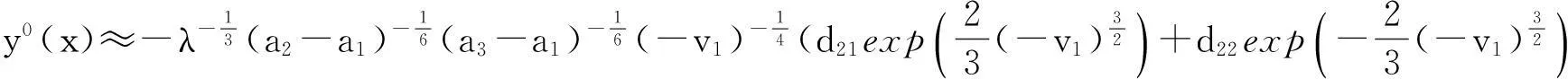

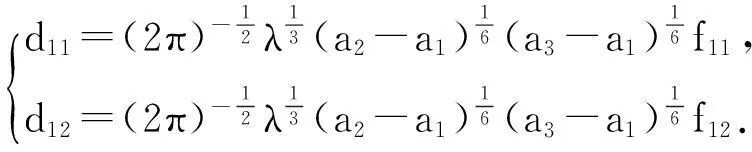
4.2 Matching near x=a2




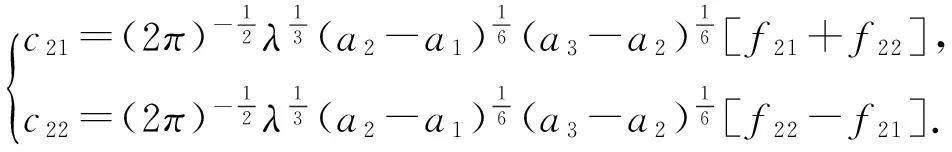


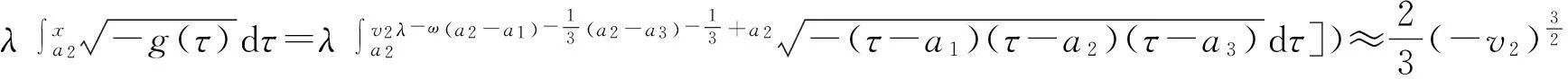


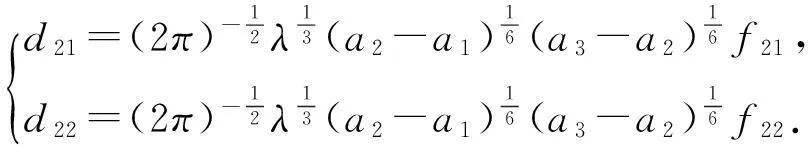
4.3 Matchingnearx=a3