射线跟踪技术中物体外形精确建模算法
周晓平, 柳朝阳
(1.郑州大学信息工程学院,郑州450001; 2.郑州大学数学与统计学院,郑州450001)
射线跟踪技术中物体外形精确建模算法
周晓平1,柳朝阳2
(1.郑州大学信息工程学院,郑州450001;2.郑州大学数学与统计学院,郑州450001)
[摘要]为了对复杂物体外形进行快速精确建模,利用多面体样条方法进行物体表面的设计及应用研究.通过对样条函数节点进行分类,给出空间中任意拓扑结构网格上样条函数组的具体构造方法.研究曲线曲面控制点与生成样条函数的节点的相互依赖关系,提出在无单位分解条件下构造具有几何不变性曲线曲面的合理化方法.通过构造控制点处多面体样条函数,生成了任意拓扑结构的连续多面体样条曲面.这样的多面体样条曲面在同样性质要求下曲面次数低,只有张量积NURBS曲面的一半;并且与细分曲面相比,所获取的物体外形表面具有坐标计算准确,中间数据较少等优点,可以用于精确构造电磁射线追踪中物体的外形.
[关键词]多面体样条; 有理函数; 任意网格; 物体外形; 射线跟踪
1引言
随着移动通信的发展, 射线跟踪技术被广泛的应用于室内定位[1]、无线网络规划[2]、电磁辐射评价[3]中.对射线跟踪中所遇到形状各异的物体,需要对其外形进行快速精确建模.近几年来,国内外许多学者[4,5]运用拓扑矩形网格上的NURBS曲面对射线跟踪技术中的物体外形进行建模.
多元样条函数曲面是另一种重要的曲面设计方法.用多元箱样条函数可设计一种特定网格上的曲面[6].细分曲面适宜于任意拓扑网格上的曲面的设计,但是个极限过程的结果,不适宜于精确的坐标计算,因此不适合电磁计算中物体外形快速精确建模.以光滑余因子协调方法[7]为核心的多元样条的代数几何方法,把任意剖分下的多元样条归结为方程组求解.但具体的解却与多元样条依赖的网格结构有关,难以有通用曲面设计方法.包含不同类型的多元样条的多面体条[8]进行曲面设计是计算几何中一个非常重要的课题,有待于进一步研究,寻找突破.
本文通过对多面体样条的节点进行分类,构造了控制点处多面体样条,生成了任意拓扑结构的连续多面体样条曲面.这样的曲面次数低,坐标计算准确等,适合电磁计算中物体外形快速精确建模,有必要深入研究其在电磁计算中的应用.
2多面体样条
2.1 单个多面体样条的构造
设P是Rn+s中以n+s-1-维超平面为边界的凸多面体,L为Rn+s到Rs的线性映射,则多元的多面体样条B(x)可定义为
B(x)=voln(P∩L-1x),x∈Rs,
(1)
其中s≥1,n≥0.
若取L=Rs为n+s-维欧氏空间Rn+s中向量到其前s-维向量的投影
Rs(x1,x2,…,xs,xs+1,…,xn+s)=(x1,x2,…,xs),
则由Rn+s中的单纯形V可定义s元n次样条函数
B(x)=voln(V∩Rs-1x),x∈Rs,
(2)
其中voln表示n-维体积,在n=1时为长度.
常见的样条函数都是多面体样条.图1示出一元一次样条B(x)的几何构造[6], 图中节点满足:t0 图1 一元一次样条函数的几何构造 由式(1)可推得多面体样条函数支撑集为supp(B)=L(P),并满足 引理[8]多面体样条B(x)是一个分片n-次多项式,并在经过其支撑集L(P)的s-1维子区域L(F)上连续阶为Cn+s-d-2,其中F为P的任意一个面,而d为L-1(L(F))的实际维数. 引理中连续阶的结论类似于一元样条的重节点处连续阶的问题.由于L-1(L(F))⊇F,而F的维数为s-1,d≥s-1,n+s-d-2≤n-1. 多面体样条重节点要求至少有s+1-个节点值在s-1-维子区域上.对s=2,等价于3个以上的节点共线. 3任意网格上多面体样条算法 构造多面体样条函数的凸多面体P有不同的类型时就可以构造出不同的多元样条,如箱样条、锥样条.但这些传统的多元样条都是定义在特定的网格上.在射线追踪技术中,必须对复杂的物体外形进行精确地建模,利用样条函数可以实现此功能,但需要找出在任意网格上构造相互关联的样条组的算法. 平面网格通常由相互交叉的直线段对平面分割形成,直线段的端点或交点称为节点,两节点间的直线段称为边. 如图2所示,平面网格中包含节点ti的最小多边形称为节点ti的支撑集合,记为supp(ti).节点ti称为supp(ti)的内(节)点.作为多边形supp(ti)顶点的n个节点ti,j(j=1,2,…,n)称为supp(ti)的(边)界(节)点.通过对节点添加分量,构造三维空间中的n+1个加长向量点(ti,j,0),j=1,2,…,n和(ti,1).如图3所示,这n+1个点构成了界点围成的平面多边形supp(ti)为底面,(ti,1)为顶点的立体锥形多面体pg(ti). 图2 平面网格的节点ti及其支撑集 图3 平面网格节点ti处多面体和样条 若能保证此锥形多面体pg(ti)每个点的投影都在底面多边形supp(ti)内,则由pg(ti)各点向底面supp(ti)投影所定义的样条Bi(t)称为ti处的二元一阶样条函数. 节点ti处的二元一阶样条函数Bi(t)的值是多面体底面上各点的高程值,是个真正的一次曲面函数.保证这个函数关系成立不需要supp(ti)为凸集. 设平面函数li,j(t)满足 li,j(ti,j)=0,li,j(ti,j+1)=0,li,j(ti)=1, (3) 即为一个过节点tij,tij+1直线方程函数,则有 定理任意网格中节点ti处的二元一阶样条函数Bi(t)可表示为 (4) 其中Δi,j表示三个节点ti,j,ti,j+1和ti给出的三角形. 4任意网格上连续性多元样条曲面设计算法 基于一元样条函数的B样条曲线具有如下表示形式和性质. (i) (整体性)B样条曲线存在于整个参数空间,具有无限的表示形式 (5) 而Bi,k(t)是相应于参数空间中给定节点序列 -∞<…≤t-1≤t0≤t1≤…≤ti-1≤ti≤…<+∞ (6) 的k-阶样条函数. (ii) (局部性)式(5)中Bi,k(t)的有界支撑集使得单独某个控制点Pi只对有限范围的P(t)有影响,使得P(t)可定义在有限范围内,可定义在在相互分离的区间段上.P(t)的计算实际上只有有限项. (iii) (光滑性)Bi,k(t)的k-1-阶光滑性保证了P(t)的k-1-阶光滑性.因此,样条函数阶数的选取直接依据对最终生成曲线的光滑性的要求而定. (iv) (非负单位分解性)式(5)中的所有k-阶样条函数Bi,k(t)满足 (7) 使得曲线P(t)具有仿射不变性和凸包性质[9].并且由于Bi,k(t)的有限支撑集,P(t)只是位于相关控制点,而非全体控制点的凸包之内,这使得P(t)具有更紧凑的凸包性质. (v) (易扩展性)实际应用中,常常给出有限个控制点Pi,并由此构造有限范围内的P(t).同时,增加或减少一个控制点只是P(t)相应地增加或减少了一段,但P(t)作为一条完整的曲线,整体性质不变. 将式(5)中的Bi,k(t)换成二元样条Bi(t),就可以构造任意网格上物体外形曲面.控制点Pi分布在网格节点处,形成与节点、二元样条Bi(t)的相互对应. 通过一个一个的多面体样条函数的性质保证网格上的所有多面体二元样条函数与曲面满足4.1小节中的性质(ii)、(iii)及(iv).如箱样条、基于单纯形剖分的多元样条基函数[9]、基于特定网格多面体区域的多元样条基函数[8].但将网格上的所有多面体样条应用于任意形状物体外形曲面设计时,要使性质(iv)成立必然会引进过多的样条函数;要使性质(v)成立,在增减一个控制点时会增减太多基函数.另外,式(7)也不能保证必然成立. (8) 如果想适当调整各个控制点的贡献大小的似然比例值,则可定义 (9) 对于有限多个控制点Pi,i∈I,可定义 (10) 但参数t的取值范围不是∪i∈Isupp(Bi,k),而是∪i∉Isupp(Bi,k)的补集.这保证了在增加控制点时新增加的曲线段、曲面片与已定义的部分既能合理拼接(保持必要的光滑性),又互不影响. 下面给出不同网格上曲面的构造模型. (i) 三角网格中的二元一阶样条函数及曲面:若所有数据已经三角化,利用此三角网格上二元一阶样条函数定义的曲面就是每个三角形的三个节点处的三个控制点为一组定义的平面三角形块组成的多面体曲面.若所有的supp(Pi)覆盖每个三角形网格恰好三次,则所有数据点处样条的和恒为1,即4.1小节的性质(iv)成立.否则,不成立. (ii) 四边形网格的二元一阶样条函数及曲面:若所有数据具有四边形剖分,则此网格二元一阶样条函数定义的曲面就是四边形每一点与其它顶点相连的平面三角形片为一组联合组成的多面体曲面,是分片连续的一次曲面.四边形剖分中网格大小可以不一致.对网格大小一致的矩形剖分数据,此曲面不同于矩形网格上笛卡尔乘积型的双一次曲面.双一次曲面是二次曲面. (iii) 任意网格的二元一阶样条函数及曲面:若所有数据具有一般的多边形剖分,则此二元一阶样条函数定义的曲面在多边形剖分内为分片连续的一次曲面组成.一次曲面的片数与描述的对角线剖分多边形区域数目相同,是随多边形边数快速增加的很大的值[10].任意网格可以包含三角、四边形,甚至其他类型的混合网格.样条函数是根据控制点定义的,不同的控制点处的样条函数网格形式是不一样的,求解结果也不一样.但依据多面体样条的定义不难统一求得. 5结论 本文提出的算法可以用于构造控制点处二元一阶样条函数,生成任意拓扑结构上连续的二元一次样条曲面;这样的多元样条函数曲面具有曲面次数低,坐标计算准确,中间数据较少等优点,非常适合电磁射线跟踪中物体外形精确构造及应用.由此可见,二阶,甚至更高阶光滑度的多面体样条,以及相应的多元样条曲面的构造方法及在工程中的应用是值得进一步研究的问题. [参考文献] [1]袁正午,王丹丹.基于射线跟踪和Voronoi图的室内定位算法[J].计算机应用研究, 2013, 30(2): 399-401. [2]霍羽, 徐钊,刘逢雪.融合波模和射线理论的矿井电波传播模型[J].电子学报, 2013, 41(1): 110-115. [3]周晓平,谭凤杰,柳朝阳,等.射线跟踪技术的一种加速算法[J].电波科学学报,2013,28(3):491-497. [4]PerezJ,CatedraMF.ApplicationofphysicalopticstotheRCScomputationofbodiesmodeledwithNURBSsurfaces[J].IEEETransactionsonAntennasandPropagation, 1994, 42(10): 1404-1411. [5]王楠,袁浩波,梁昌洪.应用NURBS-UTD方法分析受扰方向图[J].电子学报,2010,38(6): 1323-327. [6]ZhangYong-Chun,DaFei-Peng,SongWen-Zhong.PiecewiseC1surfacesbasedonbivariatequarticbox-Splinesforarbitrarytriangularmeshes[J].JournalofSoftware, 2006, 17(10): 2211-2220. [7]王仁宏. 多元齿的结构与插值[J]. 数学学报, 1975, 18: 91-106. [8]GoodmanT.Polyhedralsplines[C]∥DahmenW,GascaM,MicchelliCA.Computationofcurvesandsurfaces.Kluwer,Dordrecht,SpringerNetherlands,1990:347-382. [9]TraasC.Practiceofbivariatequadraticsimplicialsplines[C]∥DahmenW,GascaM,MicchelliCA.Computationofcurvesandsurfaces.Kluwer,Dordrecht,SpringerNetherlands, 1990:383-422. [10]LiuChao-yang.TheoryandapplicationofconvexcurvesandsurfacesinCAGD[M].ISBN90-365-1577-7,PressofUniversityofTwente, 2001. AlgorithmofPrecisionModelingBodySurfaces inElectronicRay-TracingTechnique Zhou Xiao-ping1,Liu Chao-yang2 (1.SchoolofInformationEngineering,ZhengzhouUniversity,Zhengzhou450001,China; 2.SchoolofMathematics&Statistics,ZhengzhouUniversity,Zhengzhou450001,China) Abstract:Inordertomodelthecomplexbodysurfacesinelectronicray-tracingquicklyandaccurately,thepolyhedronsplinemethodisemployedintheresearchonbodysurfacedesigningandapplication.Byclassifyingknotsrelatedtosplinefunctions,amethodispresentedforgeneratecertainsplinefunctionsoverameshwitharbitrarytopologicalstructureinspace.Theinterdependentrelationshipbetweencontrolpointsforacurveorsurfaceandthemeshknotsforsplinefunctionsisdiscussed.Thecurveorsurfacewithblendingfunctionsofnon-unitdecompositionpropertyisdesigned,withgeometricalinvarianceandconvexhullproperty.Byconstructingcontrolpolyhedronsplinefunctionsatcontrolpointsdistributedinameshwitharbitrarytopology,acontinuouspolyhedronsplinebodysurfaceoverarbitrarytopologyisgenerated.AsonlyhalforderofthecontinuoustensorproducttypeNURBSsurface,orderforthecontinuouspolyhedronsplinesurfaceislow.Comparingtosubdivisionsurfacewhichislimitingresult,thissurfacecanbeobtainedexactly,withlessprocessingdata,and,canbeusedforprecisioncomplexbodysurfacesinelectromagneticraytracing. Keywords:polyhedralspline;rationalfunction;arbitrarymeshes;bodysurface;electromagneticraytracing [基金项目]河南省重点科技攻关项目(142102210492,132102210194) [收稿日期]2014-05-08;[修改日期] 2014-11-08 [中图分类号]TP391.72;O241.3 [文献标识码]B [文章编号]1672-1454(2015)01-0021-05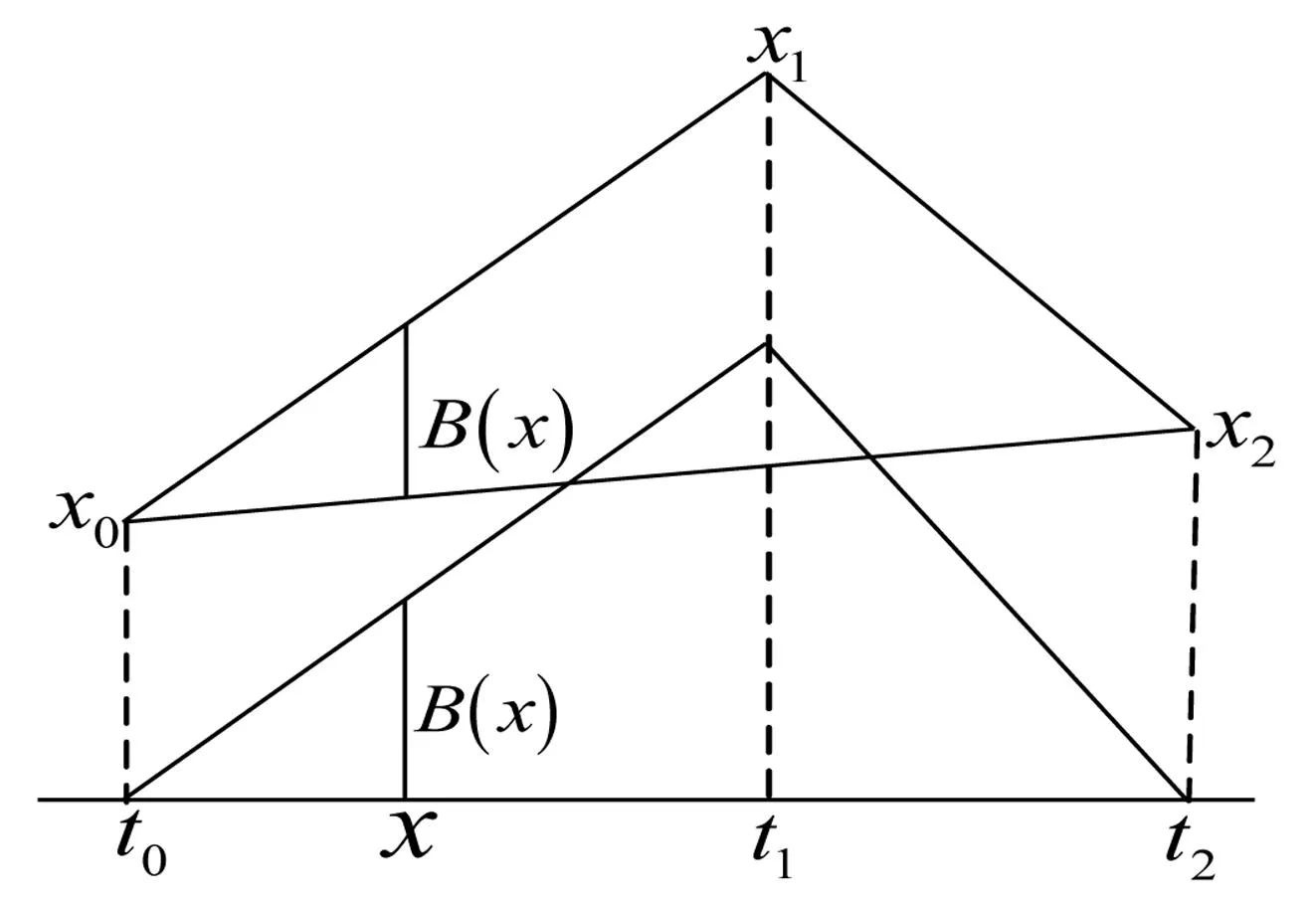
2.2 多面体样条性质
3.1 任意网格上多面体样条组的构造

3.2 任意网格上的多面体样条公式

4.1 样条函数曲线及性质
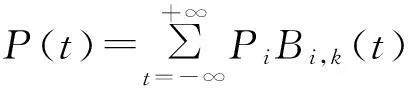
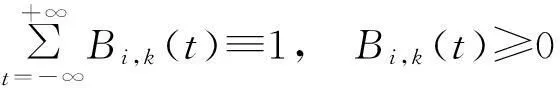
4.2 任意形状物体外形曲面算法及性质

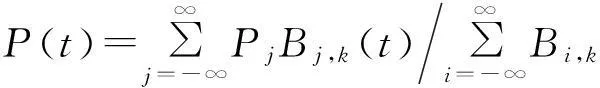
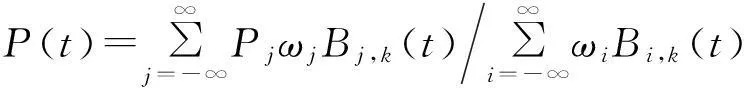
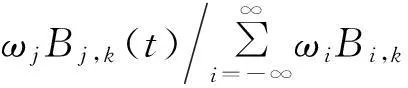

4.3 不同类型网格物体外形曲面构造算法

