二次曲线垂直切线的研究

王　庆

(苏州市职业大学数理部, 江苏苏州215104)



二次曲线垂直切线的研究

王庆

(苏州市职业大学数理部, 江苏苏州215104)

[摘要]用解析几何与射影几何的方法讨论二次曲线垂直切线交点的轨迹,重新证明了:椭圆、双曲线垂直切线交点的轨迹是圆;抛物线垂直切线的交点在准线上,且切点的连线过焦点.

[关键词]二次曲线; 射影几何; 切线

探讨平面二次曲线相互垂直切线交点的轨迹是平面解析几何的一个经典问题.文献[1] p.169 题291提出椭圆的互成直角的切线的交点轨迹是一个圆(Jes.1884).本文首先用解析几何与射影几何的方法对这一结果给出详细证明. 其次还利用射影几何的方法研究了双曲线及抛物线互成直角的切线的交点轨迹.

证法一首先用解析几何的方法讨论.

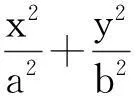
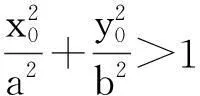
设切点是P(x1,y1)，P′(x2,y2)，则有

同理可得

直线AP，AP′成直角的条件是

(x1-x0)(x2-x0)+(y1-y0)(y2-y0)

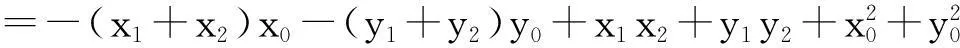
这证明椭圆相互垂直的切线的交点在圆：x2+y2=a2+b2上.

下面用射影几何的方法证明，证明的过程也给出许多几何信息.所谓射影几何的方法是把欧氏平面上的几何问题看作拓广平面上的问题，用射影几何的定理性质来解决.把欧氏平面平行的直线看做交于无穷远点，而所有无穷远点构成一条无穷远直线，可以得到拓广欧氏平面，拓广平面可以等同于射影平面.本文讨论中所用射影几何的概念性质可见文献[2].

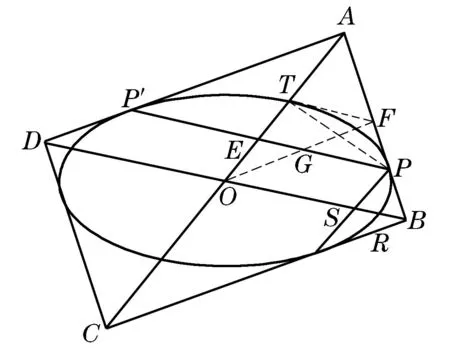
图1

证法二设ABCD是椭圆的外切矩形，P，P′分别是AB，AD上切点.由文献[2] p.186 题8，它的对角线是一对共轭直径，交点O是椭圆的中心.设线段AO交PP′与椭圆于E，T，利用仿射变换及圆的性质可以证明，OT2=OE·OA.类似设线段BO交过P，AO的平行线与椭圆于S，R，有OR2=OS·OB.

OT2=OE·OA也可以证明如下(这一方法可以用于双曲线).

设T处切线交AB于F，OF交PP′于G，不难知道TP上的无穷远点与O，F共轭，是OF的极点，TP，FG的交点是TP的中点.不难证明AC的极点是BD上的无穷远点，F在这一无穷远点与T的连线上，TF，PP′平行，因此TG，AB也平行.于是

OA∶OT=OF∶OG=OT∶OE，

因而，OT2=OE·OA.

ABCD是椭圆的外切矩形，OA=OB，PP′平行于BD，PS平行于AO，AE=EP=P′E=OS，OE=SP=SB.因此，

OT2+OR2=OE·OA+OS·OB=OA·(OE+EA)=OA2.

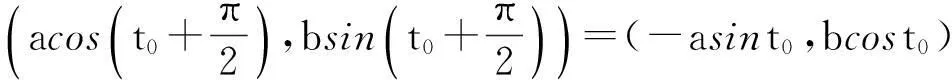
同样利用射影几何的方法, 对于双曲线可以获得如下结果.

证明类似性质1，证明中要用到下面的性质，证明留给读者.

对于抛物线相互垂直切线交点的轨迹问题有如下结果.

性质4抛物线相互垂直切线的交点在准线上，且切点的连线过焦点.

对于这一结果仍可用射影几何的方法加以证明, 关键在于抛物线的如下两个性质.

性质5设两条抛物线有相同的焦点与对称轴，过焦点的直线与抛物线交于四点，则过此四点的切线构成一个矩形，它的一条对角线过焦点(见文献[1] p.145 题2).

设∠APF=α，如图，过抛物线Γ1的顶点S作切线交PA于T.由文献[2] p.209 例5，PT⊥TF，∠SFP=2∠TFP=π-2α.同理设∠FQ′B=β，如图，过抛物线Γ2的顶点X作切线交BQ′于Y，则∠XFQ′=π-2β.从∠PFS=∠XFQ′可得α=β，直线PA与BQ′平行，ADBC是矩形，它的顶点A，B分别在抛物线Γ1与Γ2的准线上.

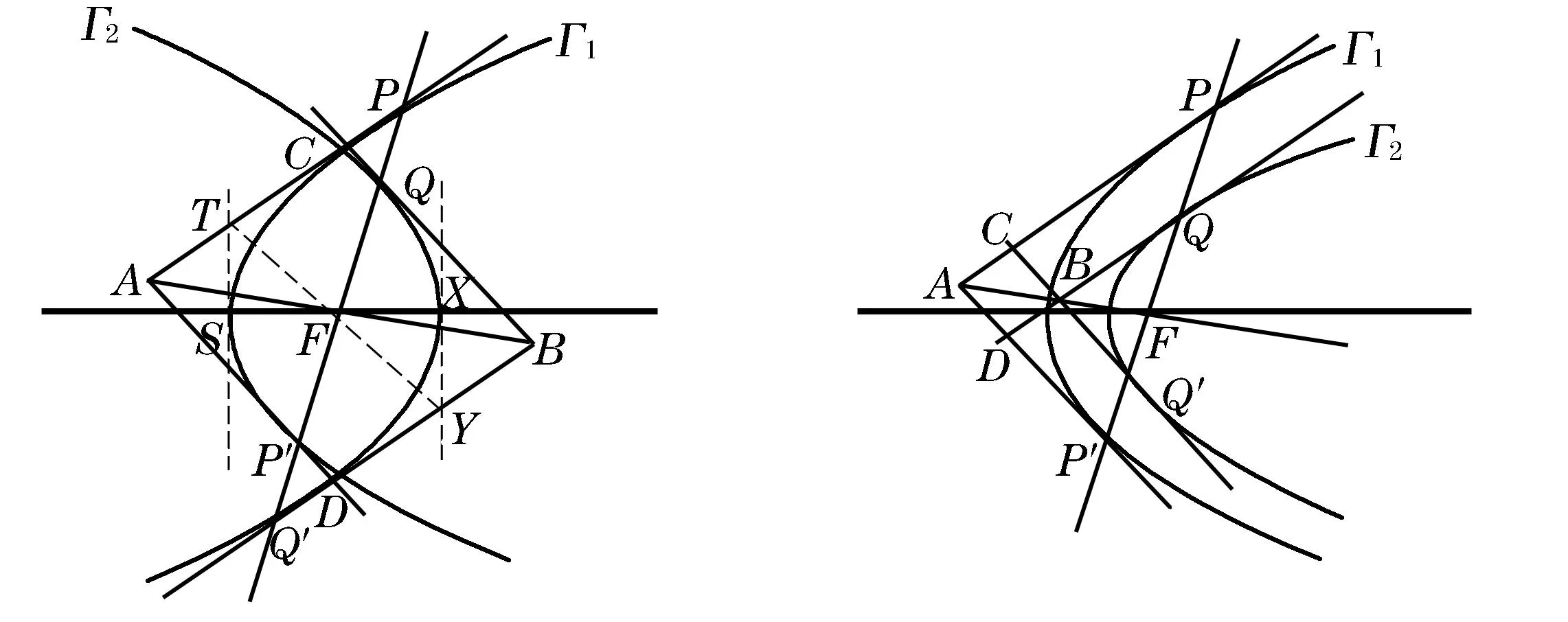
图2

性质6设A是抛物线上点B，C处切线的交点，过抛物线上点P的切线分别交AB，AC于X，Y，过P的直径交BC于Z，则AXZY是平行四边形.如果BC过抛物线的焦点，则AXZY是矩形.

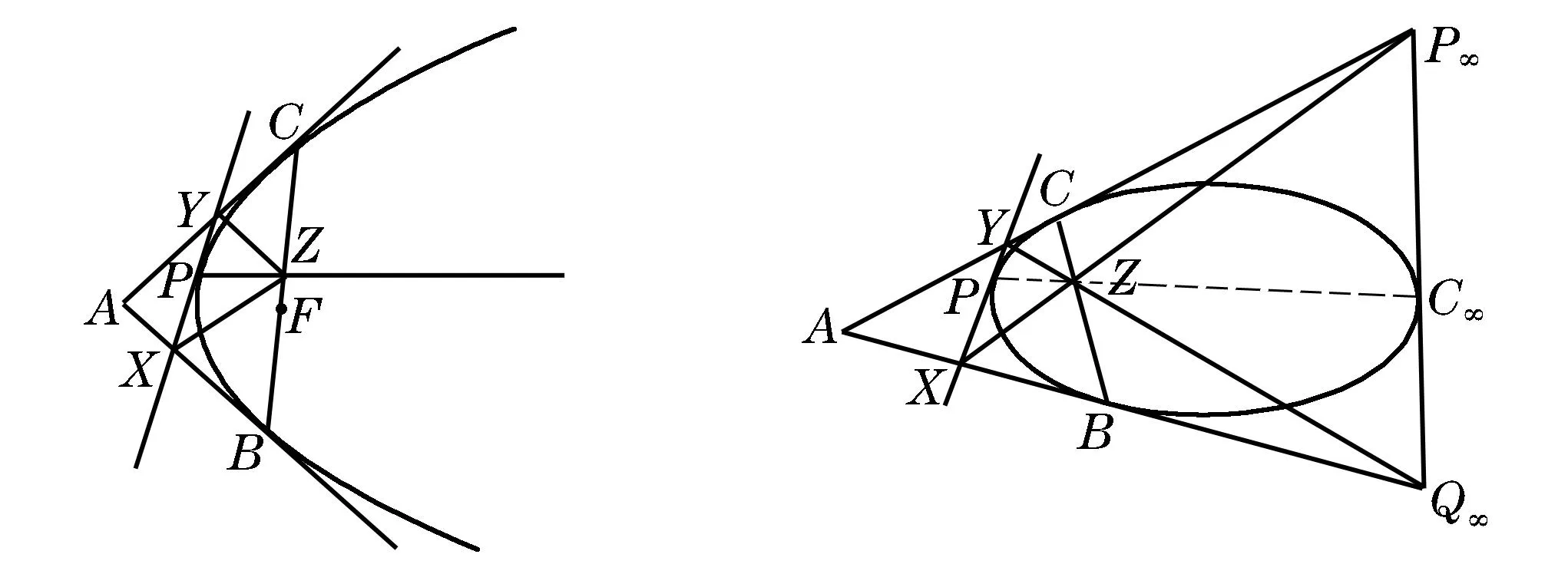
图3

[参考文献]

[1]科克肖特A，沃尔特斯F B. 圆锥曲线的几何性质[M]. 蒋声译.上海：上海教育出版社，2002.

[2]周建伟. 高等几何[M].北京：高等教育出版社, 2003.

The Study About Vertical Tangent Lines of Quadratic Curves

WANGQing

(Ministry of Mathematical and Physical, Suzhou Vocational University, Suzhou 215104,China)

Abstract:We use the method of analytic geometry and projective geometry to discuss the track of intersection point about vertical tangent lines of quadratic curves,and prove that the track of intersection point about vertical tangent lines of ellipse, hyperbolic is circle and the intersection point about vertical tangent lines of parabola is on the directrix and the connection to the point of tangency pass focus.

Key words:quadratic curve; projective geometry; tangent line

[收稿日期]2014-04-28

[中图分类号]O123.1

[文献标识码]C

[文章编号]1672-1454(2015)01-0124-03