一道数学竞赛题的探讨

王泓博

(合肥工业大学电气与自动化工程学院2012级，合肥230009)



一道数学竞赛题的探讨

王泓博

(合肥工业大学电气与自动化工程学院2012级，合肥230009)

[摘要]对浙江省高等数学竞赛题的一道试题给出了新的解法，同时提出了若干类似问题并给出解答.

[关键词]数学竞赛试题； 基本初等函数； 最大(小)值； Taylor公式； 函数单调性

1引言

2013年浙江省高等数学竞赛(文科与专科类)第三题为：

该试题的参考答案如下.

其中ξ介于0与x之间.

这道试题及解答启发我们提出如下问题：该试题是否还有其他解法？另外，若将试题中的f(x)=sinx改为其他基本初等函数(初等函数)，如cosx,tanx,ex，lnx(或ln(1+x))，arcsinx, arctanx等，是否也会产生类似问题？本文将对比展开讨论.

2试题的第2种解法

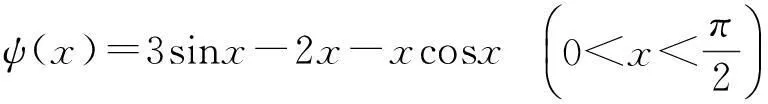
ψ′(x)=2cosx-2+xsinx,ψ″(x)=xcosx-sinx=cosx(x-tanx).

3与试题类似的问题

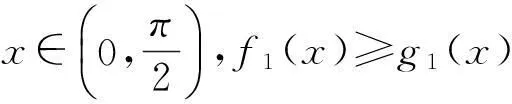
(iii) 设f3(x)=ex，g3(x)=1+x+a3x2.若对∀x>0,f3(x)≥g3(x)，求常数a3的最大值.

(iv) 设f4(x)=ln(1+x)，g4(x)=x-a4x2.若对∀x>0,f4(x)≥g4(x)，求常数a4的最小值.

(v) 设f5(x)=arcsinx，g5(x)=x+a5x3.若对∀x>0,f5(x)≥g5(x)，求常数a5的最大值.

(vi) 设f6(x)=arctanx，g6(x)=x-a6x3.若对∀x>0,f6(x)≥g6(x)，求常数a6的最小值.

由于解题方法类似，因此我们仅给出问题(ii),(iv),(vi)的解答，其余问题可供读者作为练习.

问题(ii)的解答.

故由Taylor公式知

问题(iv)的解答.

其中ξ>0.所以

问题(vi)的解答.

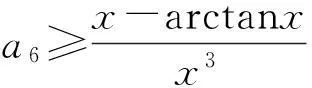
故由Taylor公式知

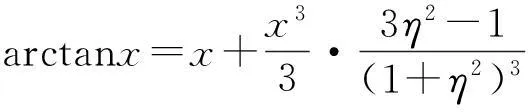
当x>0时，由于

作为本文的结束，我们还要给出两点说明.

(A) 问题(ii),(iv),(vi)的解法主要是借助于基本初函数(初等函数)的Taylor公式，若利用前面试题的第2种方法(即利用函数的单调性)也可以求解.

(B) 由于双曲函数(反双曲函数)与三角函数有相似的性质，因此对于双曲函数(反双曲函数)也会有类似的问题，例如：

设f7(x)=shx，g7(x)=x+a7x3.若对∀x>0,f7(x)>g7(x)，求常数a7的最大值；

设f8(x)=arcthx，g8(x)=x+a8x3.若对∀x>0,f8(x)≥g8(x)，求常数a8的最大值.

这些问题的解答以及尚未提出的问题及解答留给有兴趣的读者去思考.

[参考文献]

[1]同济大学数学系.高等数学(上册)[M].6版.北京：高等教育出版社，2012.

[收稿日期]2014-02-15

[中图分类号]O172

[文献标识码]C

[文章编号]1672-1454(2015)01-0102-03