椭球面上平面曲线类型的闭测地线

姜　旭,　张　量

(安徽师范大学数学计算机科学学院，芜湖241000)



椭球面上平面曲线类型的闭测地线

姜旭,张量

(安徽师范大学数学计算机科学学院，芜湖241000)

[摘要]通过对椭球面上平截线的研究, 找出了椭球面上所有平面曲线类型的闭测地线.

[关键词]椭球面; 平面曲线; 闭测地线

1引言

测地线是平面上的直线在一般曲面上的推广, 其物理意义在于光滑曲面上的质点(除约束力外,不受其它外力)的运动轨迹即为测地线[1]. 研究曲面上的测地线一直是经典微分几何的一个重要课题.熟知球面上的测地线有且仅有大圆[1], 然而对于椭球面, 情况复杂得多,文献[2]给出了推导椭球面上测地线微分方程的一种方法.今本文主要讨论椭球面上平面曲线类型的测地线, 通过研究椭球面与平面交线的几何性质, 找到了椭球面上所有平面曲线类型的闭测地线. 需要说明的是本文关于某些复杂几何量的计算中利用了数学软件Maple, 这一现代数学软件已广泛地运用于微分几何的研究中[3]. 此外本文约定三维欧式空间3中总是取直角坐标系Oxyz. 本文获得的结果具体如下.

对于旋转椭球面, 其上所有平面曲线类型的闭测地线由下述定理给出.

定理2经线和半径最大的纬圆是旋转椭球面上仅有的两类平面曲线类型的闭测地线.

2预备知识

这一部分我们回忆三维欧式空间中曲线和曲面微分几何的一些基本理论.

设α(s)是S上一条以弧长为参数的曲线, 则α的测地曲率定义为

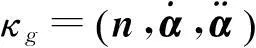
这里( , , )表示向量的混合积, “·”表示关于弧长参数的导数.特别地, 如果α的测地曲率恒为零, 则称α为S上的一条测地线[4].

设S为3中的正则曲面, r(u,v)为S的一个参数表示, 则S的单位法向量场n,可如下计算:

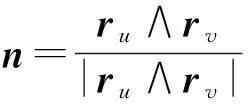
(2.1)

其中ru，rv分别为r(u,v)关于u,v的偏导数.

下面的引理告诉我们如果α的参数不是弧长参数, 仍可通过计算相应的混合积判断其是否为测地线.

引理2.1设S为3中的正则曲面,n为S的单位法向量场,又设α(t)为S上的一条正则参数曲线(t未必为弧长参数), 则α为S的一条测地线当且仅当沿着α有(n,α′,α″)=0.

证设s为α的弧长参数, 直接计算可得

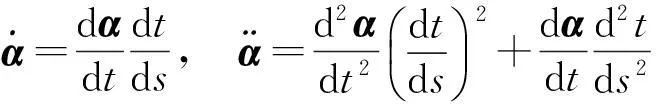
从而

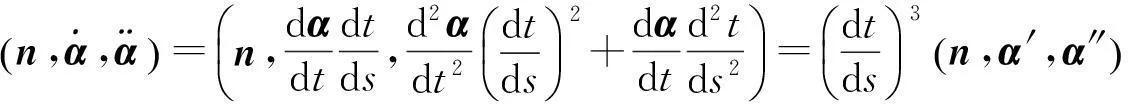
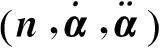
本文主要结论的证明还需要如下两个引理.

引理2.2[5]旋转曲面上的经线均为测地线, 纬圆为测地线当且仅当其上每点沿经线的切线与旋转轴平行.

引理2.3[4](Gauss-Bonnet)设S是具有定向n的正则曲面，Ω是S上的一个正则区域，边界∂Ω是由有限条互不相交的分段正则简单闭曲线C1,C2,…,Cn组成，且θ1,θ2,…,θp为C1，C2，…,Cn的所有外角，则

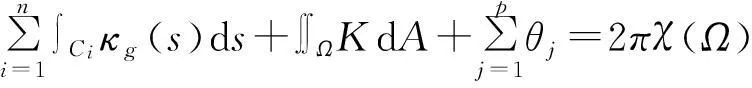
其中s为Ci的弧长参数,κg为边界了∂Ω的测地曲率，K为Ω的Gauss曲率，χ(Ω)为区域Ω的Euler示性数.

3主要结论的证明

定理1的证明设α是椭球面S上的平面曲线类型的闭测地线, 首先证明α所在的平面必过3的原点, 即椭球面中心, 否则α所在平面将椭球面分成两个大小不同的区域, 取其中较大的区域, 记为Ω. 熟知椭球面S的全曲率为∬SKdA=4π, 即

∬ΩKdA+∬SΩKdA=4π,

由椭球面的对称性并注意到Ω为椭球面上的较大区域,SΩ较小, 因此必有

∬ΩKdA>∬SΩKdA,

从而

∬ΩKdA>2π,

(3.1)

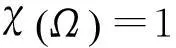
设过原点的平面π的一般方程为Ax+By+Cz=0.[6]椭球面S与平面π交线α的参数表示为[7]:

α(t)=(a(a1cost+a2sint),b(b1cost+b2sint),c(c1cost+c2sint)).

(3.2)

其中

r1=(a1,b1,c1),r2=(a2,b2,c2)

(3.3)

为齐次线性方程aAx+bBy+cCz=0的两个单位正交的解向量, 直接计算有

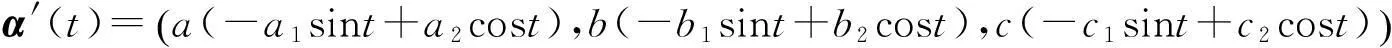
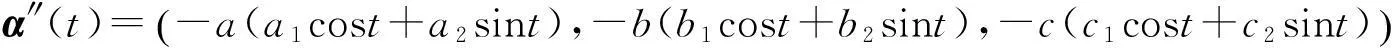
已知椭球面S的参数表示为

r(u,v)=(asinucosv,bsinusinv,ccosu),

两边分别对u，v求导可得

ru=(acosucosv,bcosusinv,-csinu),

rv=(-asinusinv,bsinucosv,0).

根据(2.1)可得

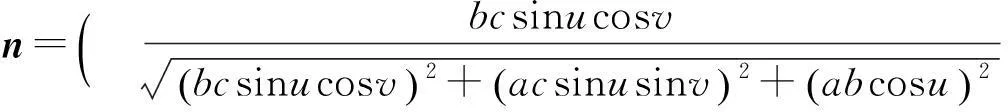
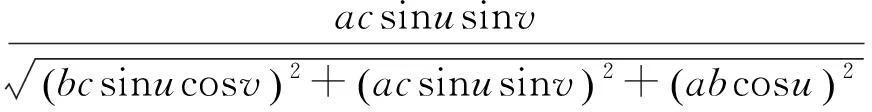
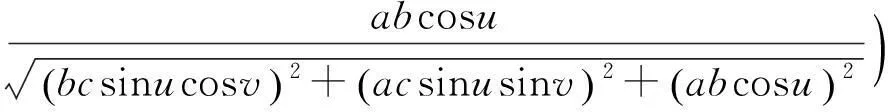
注意到α(t)为椭球面上的一条曲线, 因此存在函数u(t)和v(t)满足

a1cost+a2sint=sinu(t)cosv(t),

b1cost+b2sint=sinu(t)sinv(t),

c1cost+c2sint=cosu(t).

此时沿着平截线α变化的单位法向量可化简为

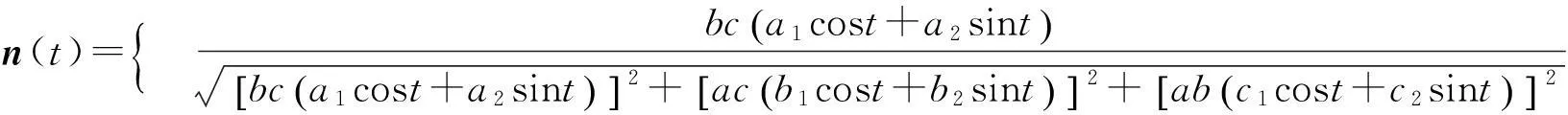
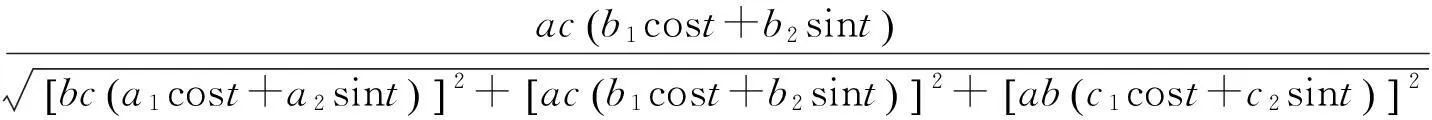
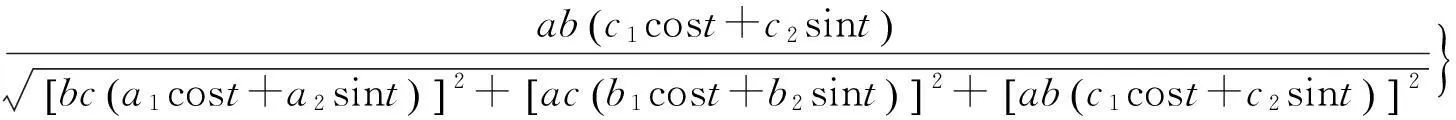
根据引理2.1可知,若曲线α为椭球面S的测地线, 则沿着α有(n,α′,α″)=0.以下利用数学软件Maple求解混合积(n,α′,α″). 方便起见, 将该混合积记为KG. 在Maple中运行程序段

>with(LinearAlgebra):

>n:=:

alpha:=:

>alphaa:=map(diff,alpha,t):

>alphaaa:=map(diff,alphaa,t):

>KG:=simplify(DotProduct(CrossProduct(n,alphaa),alphaaa,conjugate=false));

返回结果

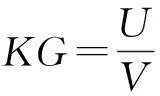
(3.4)

其中

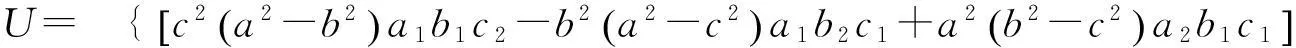
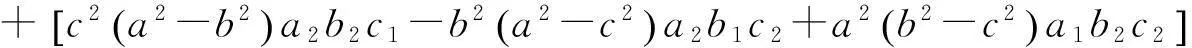
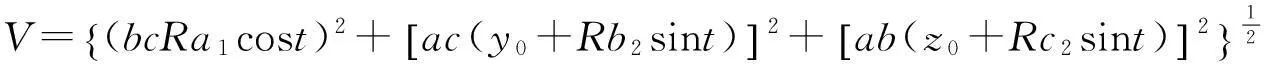
若α为测地线, 则U=0. 其充要条件为

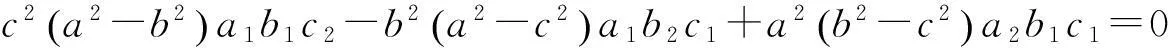
(3.5)

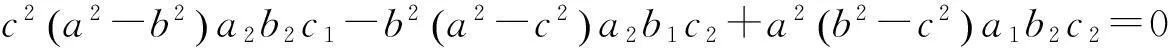
(3.6)

下面分两种情形讨论:

(i) 当A，B不同时为零时, 此时在(3.3)中取

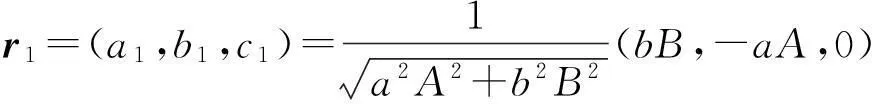
(3.7)

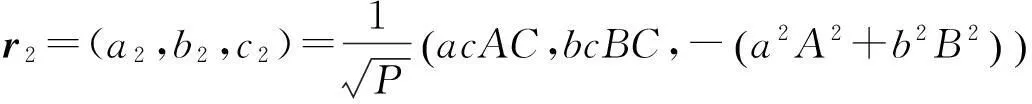
(3.8)

其中P=(a2A2+b2B2+c2C2)(a2A2+b2B2).将(3.7), (3.8)代入(3.5), (3.6), 得到

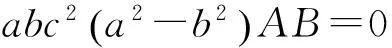
(3.9)

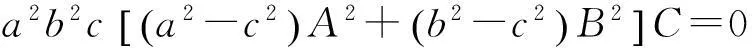
(3.10)

由于a,b,c两两互异且均大于零, 根据(3.10)知C=0或者

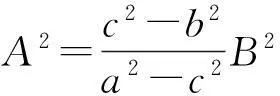
又根据(3.9)可知A，B有且仅有一个为零, 故A=C=0或B=C=0, 即交线α为椭球面与坐标轴平面xOz,yOz的交线.

(ii) 当A=B=0时, 平面π的一般方程为z=0. 此时椭球面S与平面π交线α的参数表示为α(t)=(acost,bsint,0). 此时在(3.3)中可取

a1=1,b1=0,c1=0,a2=0,b2=1,c2=0.

(3.11)

将(3.11)代入(3.5), (3.6), 可以发现两式恒成立, 因此α即椭球面与xOy平面的交线为椭球面上的测地线.证毕.

对于旋转椭球面, 由引理2.2可知其上所有的经线及最大的纬圆必为测地线, 以下可以进一步证明这两类曲线还是旋转椭球面上仅有的平面曲线类型的闭测地线.

定理2的证明设α是椭球面S上的平面曲线类型的闭测地线, 类似于定理1的证明可知α所在的平面必过3的原点, 即椭球面中心.

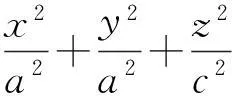
Ax+By+Cz=0.

由(3.5),(3.6)可得

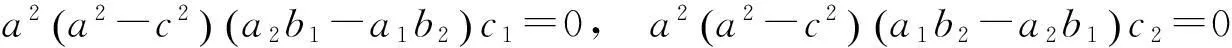
又a≠c, 且均大于零, 则

a2b1-a1b2=0,

(3.12)

或

c1=c2=0.

(3.13)

下面将分两种情形对旋转椭球面上平面型闭测地线进行分析.

(i) 当A，B不同时为零时,c2≠0,则将(3.7),(3.8)代入(3.12),可得

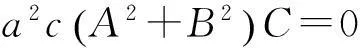
则C=0,此时交线α为椭球面与过z轴的平面的交线, 即经线.

(ii) 当A=B=0时, 将(3.11)代入(3.12),(3.13), 可以发现两式恒成立.此时交线α为椭球面与坐标轴平面xOy的交线.证毕.

[参考文献]

[1]孟道骥, 梁科. 微分几何[M]. 北京: 科学出版社, 2008.

[2]马力. 简明微分几何[M]. 北京: 清华大学出版社, 2004.

[3]John Oprea. Differential geometry and its application[M]. Washington DC: The Mathematical Association of America, 2007.

[4]Do Carmo Manfredo P.Differential Geometry of Curves and Surfaces[M]. Englewood Cliffs NJ: Prentice-Hall, Inc, 1976.

[5]黄保军. 特殊曲面上测地线的几何特征[J]. 大学数学, 2007, 28(4): 6-9.

[6]陈志杰. 高等代数与解析几何(下)[M]. 北京: 高等教育出版社, 2001.

[7]任行者, 李长文. 用代数方法确定空间圆的参数方程[J]. 淮阴师范学院教育科学论坛, 2007, 9(3):67-70.

Planar Closed Geodesics on Ellipsoids

JIANGXu,ZHANGLiang

(School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000,China)

Abstract:We determine all the planar closed geodesics on ellipsoids by studying the intersections of ellipsoids and planes.

Key words:ellipsoid; plane curve; closed geodesic

[收稿日期]2014-07-19

[中图分类号]O186.11

[文献标识码]C

[文章编号]1672-1454(2015)01-0116-05