基于华中数控宏程序三轴不等半凸型椭球曲面的加工

袁文昭

摘 要：文中介绍了运用高等数学结合解析几何等数学方法计算高精度加工半凸型椭球面的刀心轨迹方程及相应的宏程序的编程方法，提高了三轴不相等椭球面宏程序加工的精度。

关键词：加工中心；宏程序；椭球面；轨迹方程；高等数学

TG659

一、加工工藝安排

1.加工中刀具轨迹采用Z向分层法切削；

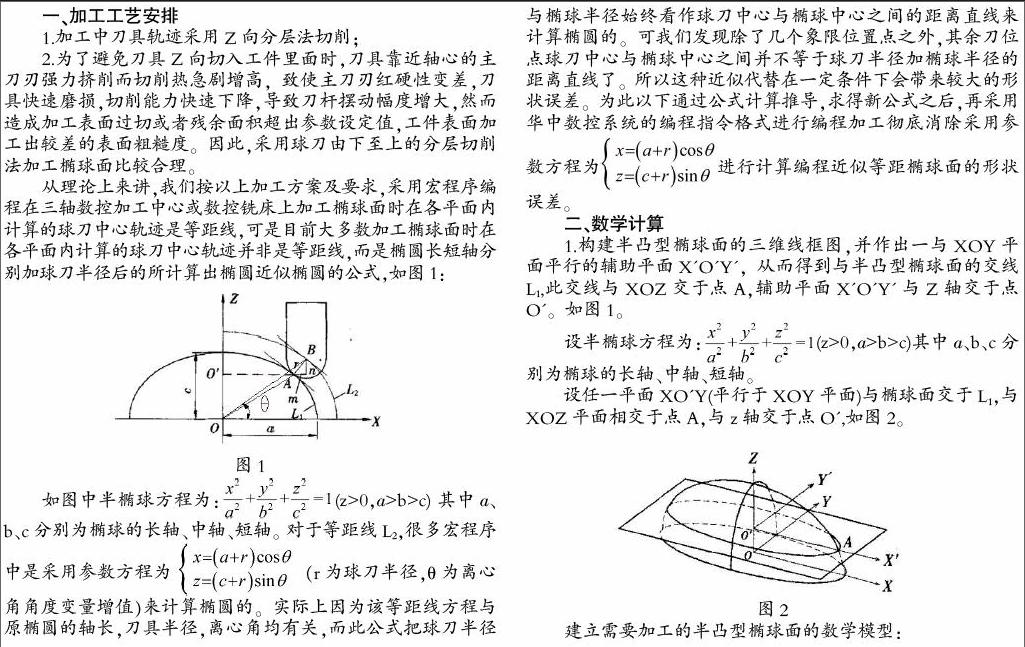
2.为了避免刀具Z向切入工件里面时，刀具靠近轴心的主刀刃强力挤削而切削热急剧增高，致使主刀刃红硬性变差，刀具快速磨损，切削能力快速下降，导致刀杆摆动幅度增大，然而造成加工表面过切或者残余面积超出参数设定值，工件表面加工出较差的表面粗糙度。因此，采用球刀由下至上的分层切削法加工椭球面比较合理。

从理论上来讲，我们按以上加工方案及要求，采用宏程序编程在三轴数控加工中心或数控铣床上加工椭球面时在各平面内计算的球刀中心轨迹是等距线，可是目前大多数加工椭球面时在各平面内计算的球刀中心轨迹并非是等距线，而是椭圆长短轴分别加球刀半径后的所计算出椭圆近似椭圆的公式，如图2

如图中半椭球方程为： （z>0，a>b>c） 其中a、b、c分别为椭球的长轴、中轴、短轴对于等距线 ，很多宏程序中是采用参数方程为 （r为球刀半径， 为离心角角度变量增值）来计算椭圆的。实际上因为该等距线方程与原椭圆的轴长，刀具半径，离心角均有关，而此公式把球刀半径与椭球半径始终看作球刀中心与椭球中心之间的距离直线来计算椭圆的。可我们发现除了几个象限位置点之外，其余刀位点球刀中心与椭球中心之间并不等于球刀半径加椭球半径的距离直线了。所以这种近似代替在一定条件下会带来较大的形状误差。为此以下通过公式计算推导，求得新公式之后，再采用华中数控系统的编程指令格式进行编程加工彻底消除采用参数方程为 进行计算编程近似等距椭球面的形状误差。

二、数学计算

四、结束语

以长轴20mm，短轴10mm的普通椭圆为例，其4mm等距线与长轴24ram，短轴14mm钧椭圆相比较，经简单测算其l，向最大误差约为0.27mm。所以在加工高精度半凸椭球面时，本文介绍的方法可以成功地解决这一问题。