带电导体为椭球体的电场分布

张拴柱

（长治学院 电子信息与物理系，山西 长治 046011）

在一般的电磁学教科书中，讨论带电导体球的例题、习题很多，但对带电椭球体的问题并没有涉及到，原因是椭球体问题需要用到的数学知识复杂一些，因此一般的电磁学教科书避而不谈。文章采用椭球坐标系，对椭球体外场的分布以及其他的一些问题展开讨论。

1 带电导体椭球体的场分布

设：在真空中有一带电量为Q的导体椭球体，其椭球面方程为：

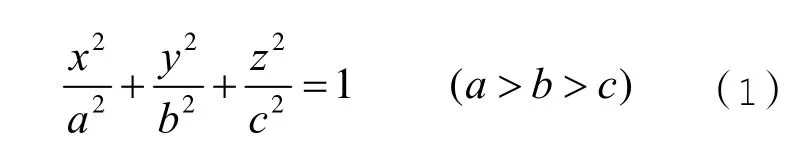
在椭球坐标系中，点M在空间的椭球坐标系，是这样的三个有序数（ξ，η，ν），它与直角坐标系的关系是：

坐标 ξ，η，ν满足

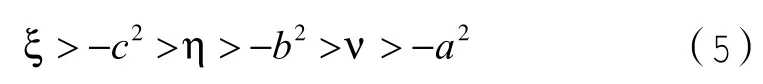
在椭球坐标系中，坐标曲面分别是：

ξ=常数：为椭球面

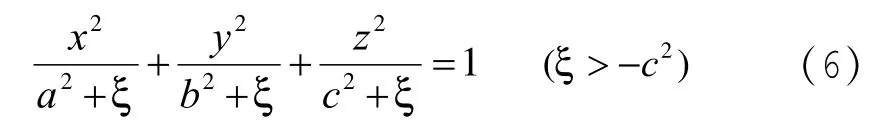
η=常数：为单叶双曲面

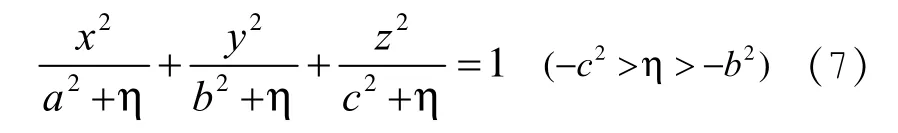
ν=常数：为双叶双曲面

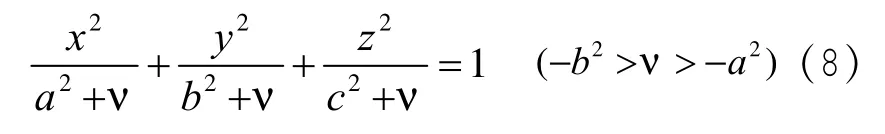
椭圆坐标系的拉梅系数

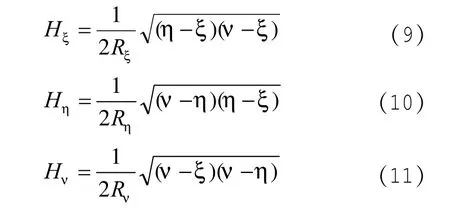
其中，

在椭球坐标系中，电势φ的拉普拉斯方程[1]为

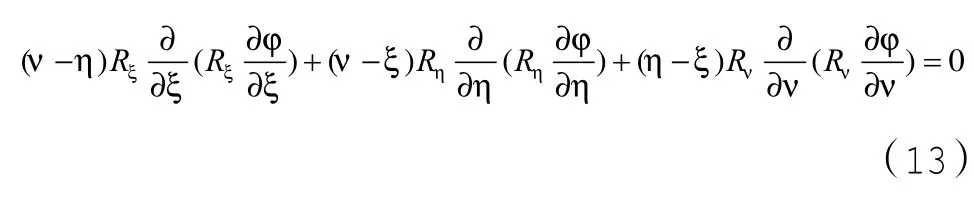
φ的边界条件是：在（1）式的椭球面上φ为常数，而在远离导体椭球非常远处φ应该趋于点电荷或带电球体、带电球面的电势。

在一族椭球面即方程（6）中，当ξ=0就是带电椭球体的椭球面方程，在椭球面上电势φc是与η、ν均无关的常量，因此，如果φ只是ξ的函数，就可以满足上面所说的边界条件。这时拉普拉斯方程（12）式变为：

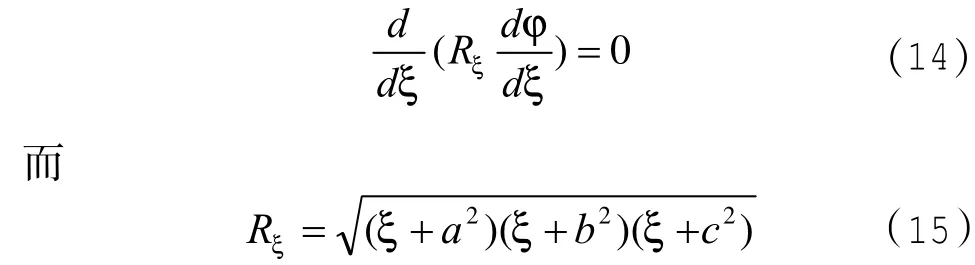
解方程（14）得：

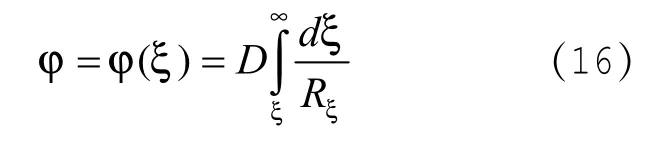
式中D是积分常数，由边界条件确定。

再由E=-▽φ可求得电场强度为：

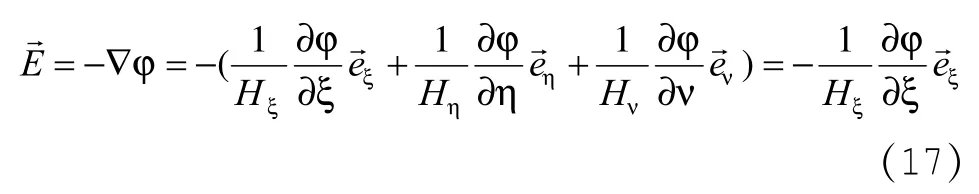
由（16）式可得：

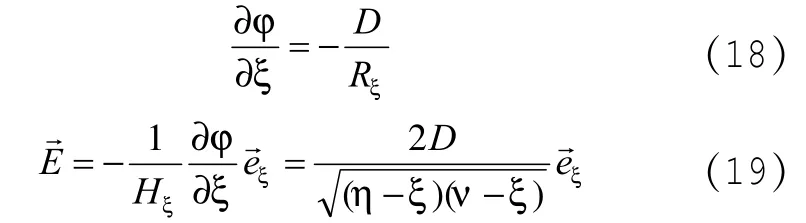
电势等势面：

由于 φ=φ（ξ）只是一元函数，当 φ= 常数时，则一定有ξ=常数，而ξ=常数，则为一族椭球面组成

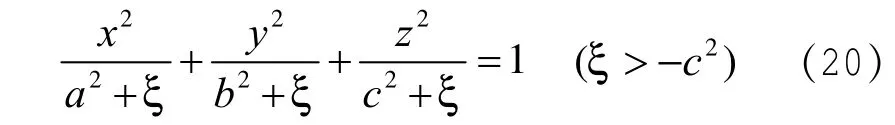
即上式为所求的电势等势面。

电力线：

由正交曲线坐标系知识可知，电力线应该满足微分方程

由于 Eη=0，所以 dη=0，则 η=常数，而 η=常数，对应是一族单叶双曲面

同理，由于 Eν=0，所以 dν=0，则 ν=常数，而 ν=常数，对应的是一族双叶曲面

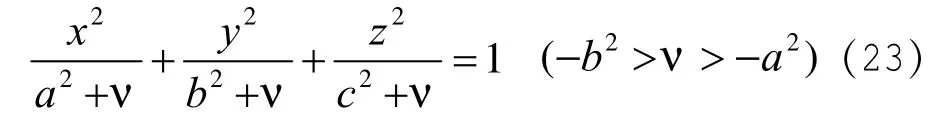
而式（22）和（23）组成联立方程，即两族曲面的相交线就是所求的空间电力线的分布函数。

下面把电势、电场强度表达式由椭球面坐标系改写为直角坐标系，并且确定积分常数D。

由正交曲线坐标系变换规则[3]可知，

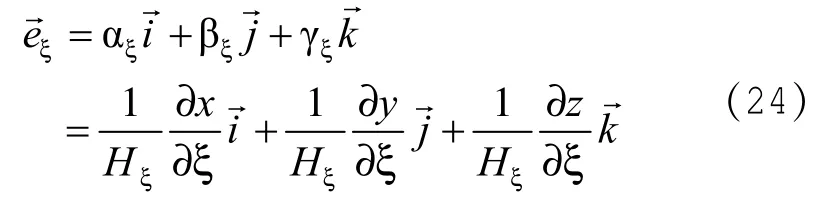
由（2）式和（9）式可求得：

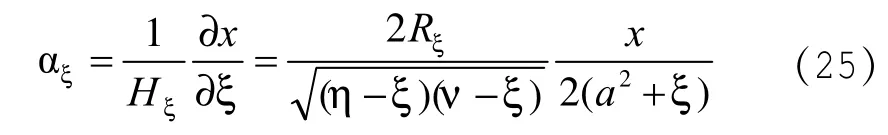
同理，根据（3、（4））和（10）、（11）式可求得：

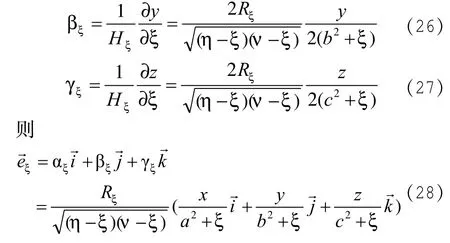
由（19）式得：

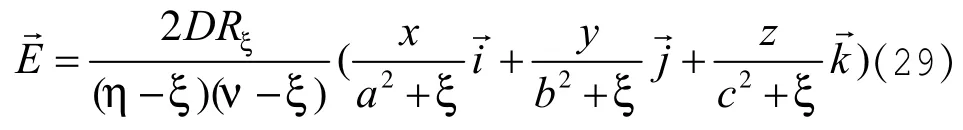
若场点在椭球面上时，取ξ=0，

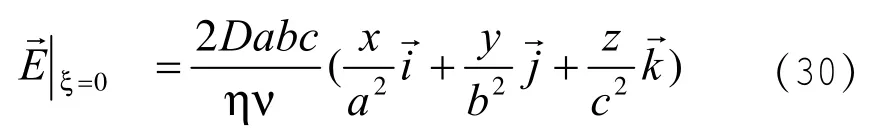
把 η，ν换成 x，y，z表示出来

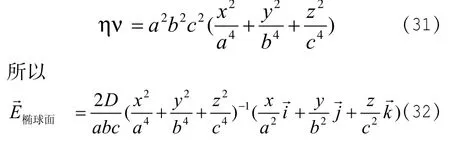
上式过渡的球面时，则取a=b=c=R

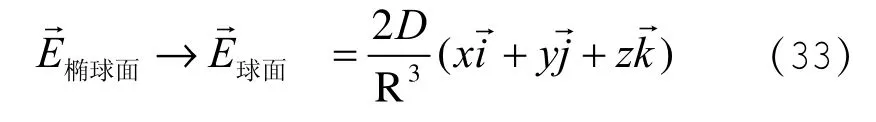
而半径为R的带电荷Q的球面公式

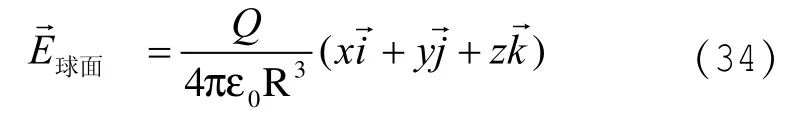
（33）式（34）比较可得：

（35）式代入（16）、（19）和（29）式，至此可写出椭球体外电势和电场强度公式

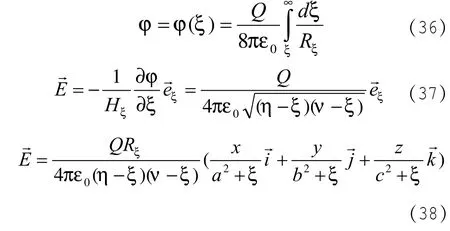
由（38）式进行一些讨论：

当ξ=0时，即是带电导体椭球面任一点的场

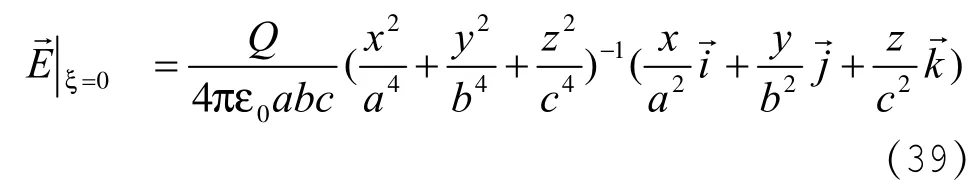
当ξ=ξ时，即ξ取任意一个值时，则它代表的是一族椭球面中的某一个椭球面，而在这个椭球面上任一点的场可以表达为：

其实（40）式就是把（38）式中的η和ν用ξ表示出来了。而ξ的意义根据文献[2]可知，与（1）式共焦的二次曲面

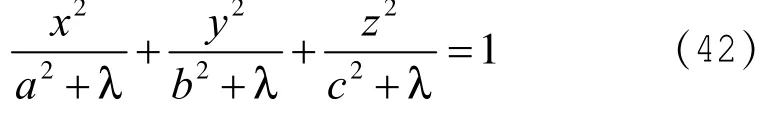
中，λ的三个互不相等的实根，三个实根大小次序选为ξ＞η＞ν，经过空间任一点的三个曲面（42），其中对应于λ=ξ的一个根是椭球，对应于λ=η的一个根是单叶双曲面，对应于λ=ν的一个根是双叶双曲面[2]。

2 带电导体椭球面上的电荷分布

由电磁场边值关系

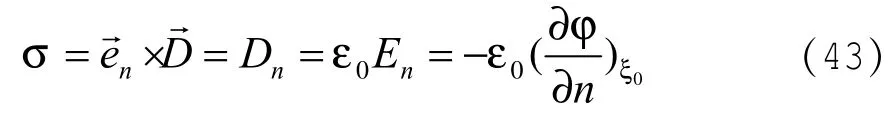
由（9）、（18）、（35）式得：

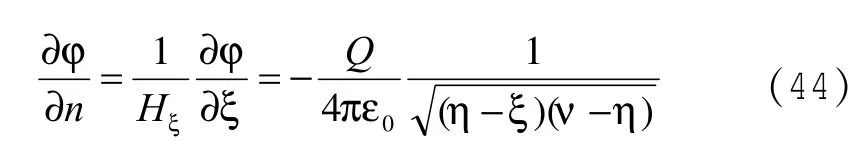
代入（43）式得：

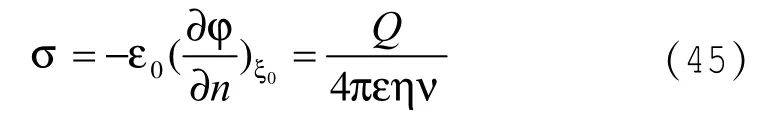
（31）代入（45）式得：

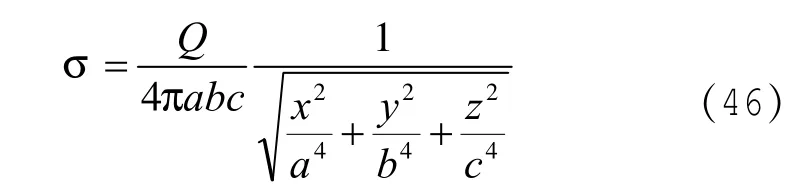
几个特殊点的情况：

（1）在x轴上两个端点，即x=±a，y=z=0

（2）在y轴上两个端点，即y=±b，x=z=0

（3）在z轴上两个端点，即z=±c，x=y=0

由此看出，因为a＞b＞c，所以曲率大的地方，电荷密度越大，如x轴两端点，反之，曲率小的地方，电荷密度越小，如z轴两端点。

如果是球体时，x2+y2+z2=R2，a=b=c=R 则

3 两个同焦点椭球面组成电容器的电容量

若有两个同焦点带电导体椭球面构成的电容器，方程为：

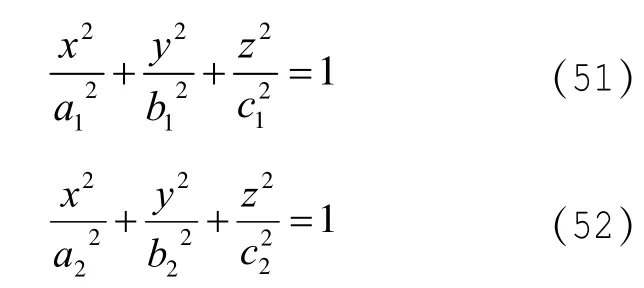
由（36）式可知，

第一个椭球面的电势，注意：

第二个椭球面的电势，注意：

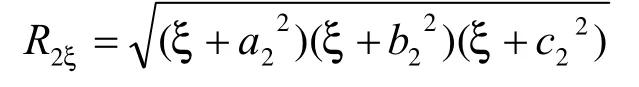
所以椭球面构成电容器的电容量

特殊情况下，当a1=b1=c1=R1，a2=b2=c1=R2即两个同心球面构成的电容器

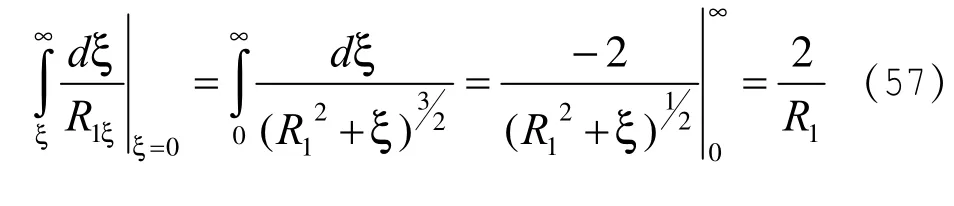
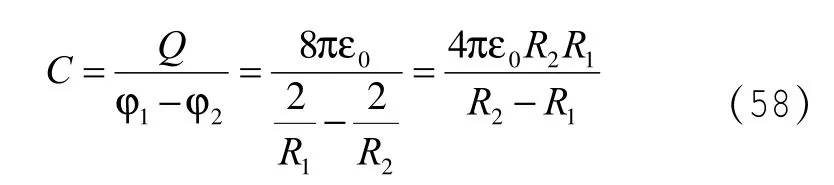
回到一般教科书上的结果。