运用Matlab讨论椭球面性质

杨　慧，　王新年

(太原师范学院几何代数研究室，太原030001)



运用Matlab讨论椭球面性质

杨慧，王新年

(太原师范学院几何代数研究室，太原030001)

[摘要]椭球面是测绘学物理学中常用的曲面之一.本文通过运用Matlab强大的绘图功能和设计技巧,用四种方法绘制了三轴椭球面,设计了平行截割法研究曲面形状的程序,且在Matlab中实现了椭球面的切平面与法线的设计,另外依据软件采用矩阵处理问题特点，实现了椭球面生成过程的动画设计.通过运行程序，表明运用Matlab可以得到生动、逼真的曲面动态图形.

[关键词]Matlab; 椭球面; 平行截割法; 动态图形

1引言

Matlab是一个交互式的系统，编程以矩阵为基本数据单元，按照IEEE的数值计算标准进行计算的，它将编辑、编译、链接、执行融为一体.它除了包含丰富的数学软件外，还包括信息工程和控制工程等方面的内容，如信息处理、小波分析、鲁棒控制等等.另外该软件具有强大的数据可视化功能，能方便地绘制各种复杂的二维、三维和多维图形，自带许多绘图函数，可以设置视角、关照效果，还可创建动画效果，对我们研究曲面性质起到了重要的作用.

下面将在Matlab中实现对椭球面性质的研究.

2在Matlab中绘制椭球面图形

在空间直角坐标系下，椭球面的标准方程为

(1)

其中a,b,c为正实数.

椭球面也称为椭圆面，其参数方程为

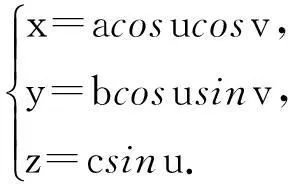
文中以a=3;b=2;c=1为例来绘制椭球面.

2.1　在Matlab中运用特殊曲面绘制函数ellipsoid实现图形绘制(如图1)

Input(′a=′);input(′b=′);input(′c=′); Input(′N=′);

[x,y,z]=ellipsoid(0,0,0,a,b,c,N)%[X,Y,Z]=ELLIPSOID(XC,YC,ZC,XR,YR,ZR,N) center(XC,YC,ZC) and semi-axis lengths (XR,YR,ZR)

surf(x,y,z)；legend(′椭球面′)；axis equal

2.2　在Matlab中绘制参数方程形式下的曲面图形

t=0∶pi/30∶2*pi;

[u,v]=meshgrid(t,t);

x=3*cos(u).* cos(v);

y=2*cos(u).* sin(v);

z=sin(u);

figure; surf(x,y,z)

axis equal

2.3　利用线性变换法：先做出球面的图形然后再代换即可 (如图2)

[x,y,z]=sphere(30);

surf(x,y,z);

axis equal

mesh(3*x,2*y,z)

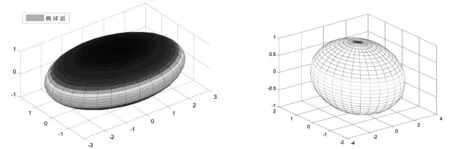
图1　　　　　　　　　　　　　　　　　　　　　　　　图2

2.4　用Matlab中绘制隐函数方程下的图形——先绘制椭球面的上半曲面，然后利用对称性绘制下半部分曲面

a=3;b=2;c=1;N=30;

xgrid=linspace(-a,a,N);

ygrid=linspace(-b,b,N);

[x,y]=meshgrid(xgrid,ygrid);

z=c*sqrt(1-y.*y/b∧2-x.*x/a∧2); m=1;

z1=real(z);

for k=2∶N-1

for j=2∶N-1

if imag(z(k,j))~=0 z1(k,j)=0;

else if all(imag(z([k-1∶k+1],[j-1∶j+1])))~=0 z(k,j)=NaN;

end

end

surf(x,y,z1),hold on

if m==1 z2=-z1; surf(x,y,z2);

end

xlabel(′x′),ylabel(′y′),zlabel(′z′)

注指令plot3实际上是二维图形绘制指令plot在三维空间的扩展,绘制的是多条曲线;指令mesh绘制的是网格曲面,该曲面将邻接的点用直线连接起来,从而形成网状曲面；指令surf绘制的是表面图,各线条之间的空挡用颜色填充.

3在Matlab中实现椭球面性质研究

椭球面有很好的对称性,是有界曲面.他与三个对称平面的交线都是椭圆,且曲面上的点(除了六个顶点)都是椭圆点,是个有心二次曲面.

3.1　Matlab中做出椭球面与一族平行平面的截线,通过研究截线的形状、大小及位置的变化研究曲面的方法称为是平行截割法.

a=3;b=2;c=1;u=0.5;

t=-3∶.2∶3;

[x,y]=meshgrid(t);

z1=u*ones(length(t));

axis equal ;

subplot(2,2,1),

surf(x,y,z1);%绘出平面图形

hold on

[x,y,z2]=ellipsoid(0,0,0,3,2,1,30);%绘出椭球面图形

surf(x,y,z2);

zoom on%容许对图形放大

xlabel(′x′);

ylabel(′y′)

zlabel(′z′);

colormap(jet),

r0=abs(z1-z2)<=0.01;

zz=r0.*z1;xx=r0.*x;yy=r0.*y;

subplot(2,2,2),

h1=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),′-′); %绘出椭球面与平面的交线

set(h1,′markersize′,0.1),hold on ,grid on

for i=1∶9,

v=1-i*0.2;t=-3∶.2∶3;

[x,y]=meshgrid(t);

z3=v*ones(size(x));

subplot(2,2,3),

surf(x,y,z3);

[x,y,z2]=ellipsoid(0,0,0,3,2,1,30);

hold on

mesh(x,y,z2);

hidden off,

colormap(hot)

r1=abs(z3-z2)<=0.01;

zzz=r1.*z3;xxx=r1.*x; yyy=r1.*y;

subplot(2,2,4),

h2=plot3(xxx(r1~=0),yyy(r1~=0),zzz(r1~=0),′b-′);

set(h2,′markersize′,0.1),hold on,grid on

end

从以上图形中可以直观地看出截线是一系列椭圆,所以椭球面可以看作一系列椭圆所生成

3.2　椭球面上一点处的切平面及法线方程

由于椭球面上的点都是椭圆点,即都是正常点，故每一点处的切平面均存在.(图4)

syms x y z;

f(x,y,z)=x∧2/9+y∧2/4+z∧2-1;

图4

nv=jacobian(f,[x y z]);

[x,y,z]=ellipsoid(0,0,0,3,2,1,20);

surf(x,y,z)

x=2;y=-4/3;z=1/2;

nv=double(subs(nv));

hold on

quiver3(x,y,z,nv(1),nv(2),nv(3),.5);

t=-1∶.2∶1;

[xx,yy]=meshgrid(t+x,t+y);

zz=-(nv(1)*(xx-x)+nv(2)*(yy-y))/nv(3)+z;

mesh(xx,yy,zz);

xlabel(′x′);ylabel(′y′);zlabel(′z′);

3.3　椭球面的表面面积

syms u v a b c

r=[a*cos(u).*cos(v),b*cos(u).*sin(v),c*sin(u)];

ru=[diff(r(1),u),diff(r(2),u),diff(r(3),u)]；

rv=[diff(r(1),v),diff(r(2),v),diff(r(3),v)]；

N=cross(ru,rv)；

M=norm(N)

运行结果为

M=a*b.*cos(u).*sqr(sin(u)∧2+c∧2/a∧2.*cos(u)∧2.*cos(v)∧2+c∧2/b∧2*cos(u)∧2sin(v)∧2

a=3;b=2;c=1;

fun=@(u,v) a*b.*cos(u).*…

sqrt(sin(u).∧2+(c/a.*cos(u).*cos(v)).∧2+(c/b.*cos(u).*sin(v)).∧2)

S=8*quad2d(fun,0,pi/2,0,pi/2)

运行结果为

S=48.8821

3.4　椭球面的体积

由前面的性质1可知，用平行于xOy面的平面z=h (-c≤h≤c)截椭球面时,截口为椭圆,该椭圆方程为

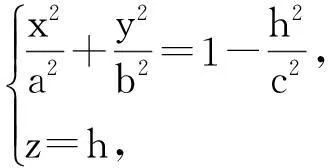
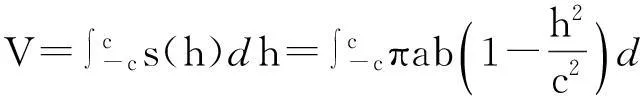
Matlab编程为：

a=3;b=2;c=1;

syms h

f=@(h) pi*a*b*(1-(h./c).∧2)

V=quad(f,-c,c)

运行结果为：V=25.1327

4Matlab中实现椭球面生成过程

4.1　旋转椭球面动态图形——依次画出曲面矩阵的各列实现

t= 0∶pi/30∶2*pi;

[u,v]=meshgrid(t,t);

x=3 * cos(u).* cos(v);

y=2 * cos(u).* sin(v);

z=sin(u);

axis([-4 4 -3 3 -2 2]);

hold on;

m=size(z,2);

for i=2∶m

plot3(x(i,∶),y(i,∶),z(i,∶));drawnow; pause(0.3);

end

注以上绘制的是坐标曲线v-曲线族,当n=m/4时，运行程序

for i=2∶n

plot3(x(i,∶),y(i,∶),z(i,∶));drawnow; pause(0.3);

end

则得到椭球面的部分曲面图(图5).

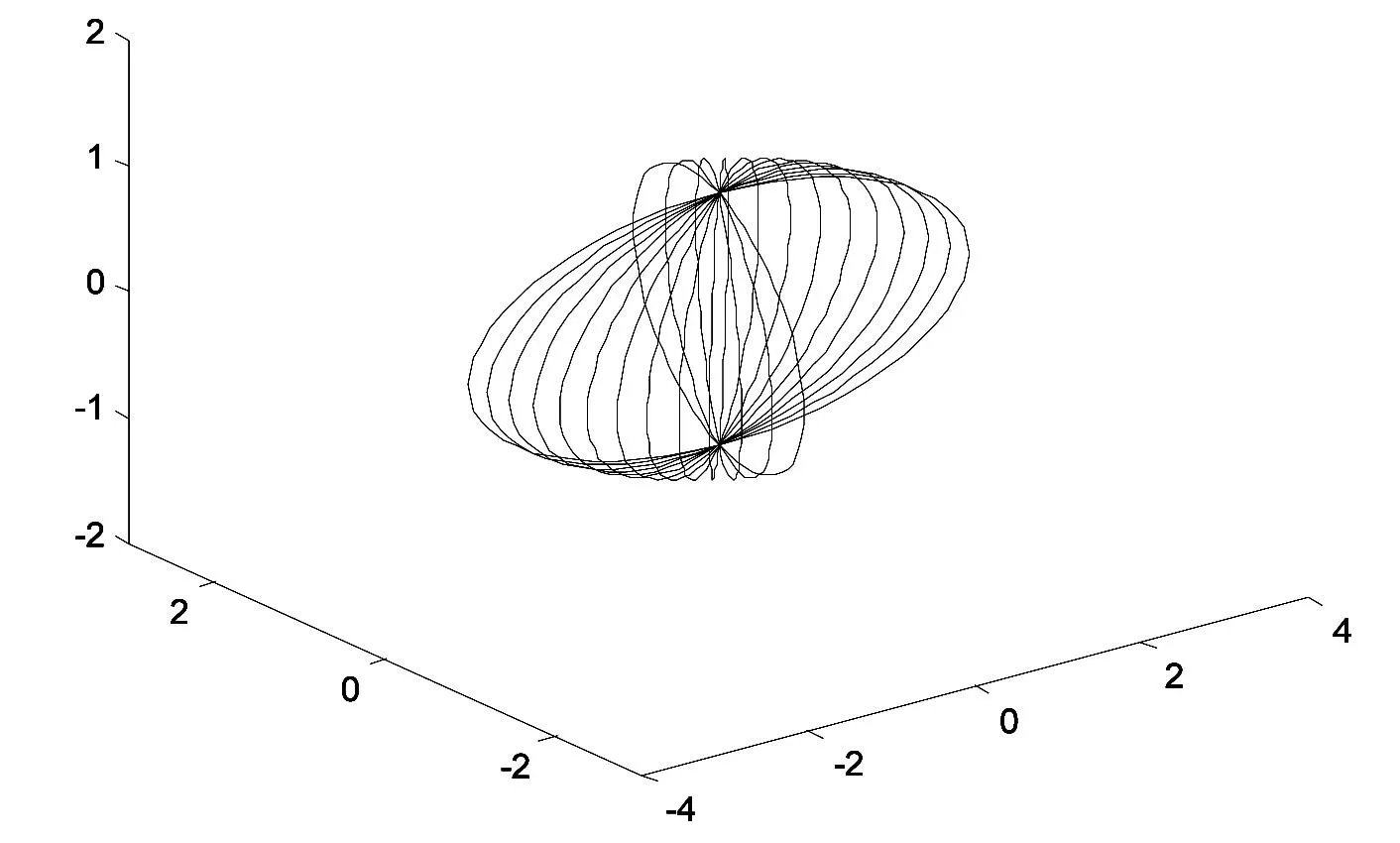
图5

for i=2∶m

plot3(x(∶,i),y(∶,i),z(∶,i));drawnow; pause(0.3);

end

注以上绘制的是坐标曲u-曲线族,当n=m/2时，运行程序

for i=2∶n

plot3(x(∶,i),y(∶,i),z(∶,i));drawnow; pause(0.3);

end

则得到椭球面的部分曲面图(图6).

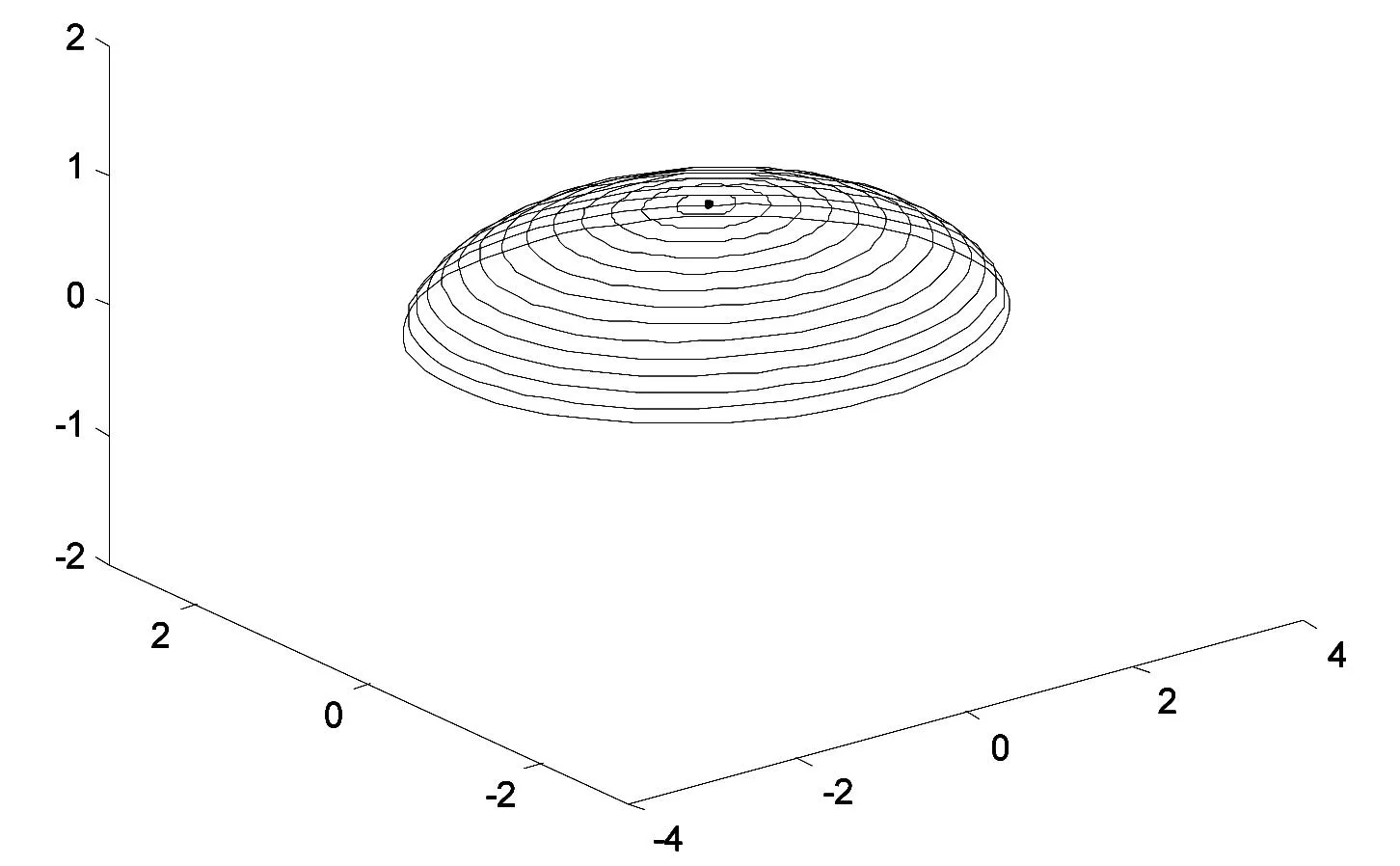
图6

4.2　椭球面动态图形——依次画出相邻两列的曲面片

for i=2∶n

surf(x(i-1∶i,∶),y(i-1∶i,∶),z(i-1∶i,∶));drawnow; pause(0.3);

end

注以上绘制的是相邻坐标曲线v-曲线构成的曲面片

for i=2∶n

surf(x(∶,i-1∶i),y(∶,i-1∶i),z(∶,i-1∶i));drawnow; pause(0.3);

end

注以上绘制的是相邻坐标曲线u-曲线构成的曲面片

4.3　椭圆绕轴旋转生成的旋转椭球面——通过做几何变换

考虑椭圆

M0=[0 0 0];L=[0 0 1];

theta=0∶pi/10∶2*pi;

y1=2*cos(theta);z1=sin(theta);x1=0*ones(1,length(theta));

plot3(x1,y1,z1)

alpha=pi/60;

I=ones(length(theta),1);

u=[x1;y1;z1];

U=ctranspose(u);V=horzcat(U,I);

for i=1∶120

A=[cos(i*alpha),sin(i*alpha),0,0;-sin(i*alpha),cos(i*alpha),0,0;0,0,1,0;0,0,0,1];

W=V*A;

mesh([W(∶,1),U(∶,1)],[W(∶,2),U(∶,2)],[W(∶,3),U(∶,3)]);

colormap(jet); hold on; pause(0.1)

drawnow;

end

在以上程序的基础上,我们可以改动几何变换矩阵做出椭圆绕任意直线生成的旋转曲面的动态图形,也可设计出空间任意曲线绕一直线旋转生成曲面的程序.

依据Matlab软件数据可视化特点,以椭球面为研究对象，研究了椭球面的性质，特别采用平行截割法对曲面的生成过程进行了程序设计,研究过程中涉及的方法技巧具有一定的指导意义,我们可以用相似的方法研究其它的曲面如双曲面、抛物面等.另外,Matlab软件拥有图像处理工具箱,提供了大量的用于图像处理的函数,可以对图像和视频进行采集，并对图像的进行变换、增强和边缘检测,希望能进一步运用它来处理几何中的各类复杂曲线曲面.

[参考文献]

[1]吕林根,许子道.解析几何[M].4版.北京：高等教育出版社,2006.

[2]赵海滨.MATLAB应用大全[M].北京：清华大学出版社,2012.

[3]任明慧.MATLAB在空间图形中的动态应用[J].数学理论与应用,2008，28(1)：40-44.

[4]向修栋,付云芝.在MATLAB中实现旋转曲面的动画设计[J].计算机技术与发展,2011,21(3)：52-55.

[5]赵亚男,牛言涛.MATLAB在解析几何教学中的应用[J].长春大学学报,2011，21(4)：54-58.

[6]孔祥强.MATLAB软件在空间解析几何教学中的应用探索[J].计算机应用与软件,2012,29(8)：297-300.

Discussing Ellipsoid Properties by Using Matlab

YANGHui，WANGXin-nian

(Geometric and Algebra Laboratory,Taiyuan Normal University,Taiyuan 610500,China)

Abstract:The ellipsoid is one of the curved surface in surveying and mapping science,physics. In this paper,by using the powerful drawing graphics and designing skills,four methods are used to draw the three-axis ellipsoid. The program of parallel cutting method is designed to study surface shape,and a tangent plane and normal are analyzed. In addition,on the basis of data processing techniques of using matrix characteristics,implements the ellipsoid generation process of animation design. By running the program,it shows that the vivid and perfect animations surface can been formed based on Matlab.

Key words:Matlab; ellipsoid; parallel cutting method; animation graphical

[中图分类号]G642.0

[文献标识码]C

[文章编号]1672-1454(2015)05-0120-07

[收稿日期]2015-04-27