哈密尔顿-凯莱定理在多项式矩阵上的推广

胡建华，　王资敏，　曾博文

(上海理工大学理学院,上海200093)



哈密尔顿-凯莱定理在多项式矩阵上的推广

胡建华，王资敏，曾博文

(上海理工大学理学院,上海200093)

[摘要]哈密尔顿-凯莱定理是高等代数中一个经典的结论，它揭示了方阵和它对应的特征多项式之间的关系. 本文将此定理推广至多项式矩阵上，给出了多项式矩阵及其行列式之间的一种关系，使经典的哈密尔顿-凯莱定理成为本文中定理的一种特殊情况.

[关键词]哈密尔顿-凯莱定理； 多项式矩阵； 伴随矩阵

1引言

哈密尔顿-凯莱定理是高等代数中一个经典的结论， 它揭示了方阵和它对应的特征多项式之间的关系，是特征多项式所具有的一个重要性质.它在线性空间的直和分解、计算逆矩阵、矩阵多项式等方面有重要的应用.在教材[1]P297中给出了此定理的内容和证明.定理可简洁地概括为:任意数域上的方阵满足其特征方程.即设A是数域上的一个n阶方阵，f(x)=det(xE-A)为A的特征多项式，则f(A)=O(零矩阵).在文献[2,3,4]中，Kaczorek将此定理推广至m×n矩阵、Block矩阵上；文献[5]中WeiXing将哈密尔顿-凯莱定理推广至多元有理矩阵上.这里我们将此定理推广至多项式矩阵上， 给出了多项式矩阵及其行列式之间的一种关系，使经典的哈密尔顿-凯莱定理成为本文中定理的一种特殊情况.

2主要结果

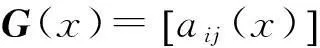
引理1存在(m+1)个n阶常数矩阵A0,A1,A2,…,Am使得

G(x)=A0+A1x+A2x2+…+Amxm.

aij(x)=aij0+aij1x+aij2x2+…+aijmxm∈[x]，i,j=1,2,…,n，

由矩阵加法和数乘运算的线性性，只需取Ak=[aijk]n×n，k=0,1,2,…,m.

注1在引理1中

G(x)=A0+A1x+A2x2+…+Amxm，

实际上G(x)也可表示成

G(x)=A0+xA1+x2A2+…+xmAm

的形式.这里采用

G(x)=A0+A1x+A2x2+…+Amxm

这种形式.这样任意给定n阶方阵A，G(A)=A0+A1A+A2A2+…+AmAm为n阶方阵.

记f(x)=det(G(x))表示多项式矩阵G(x)的行列式.

引理2f(x)∈[x]且次数不超过mn.

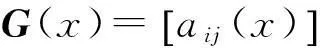
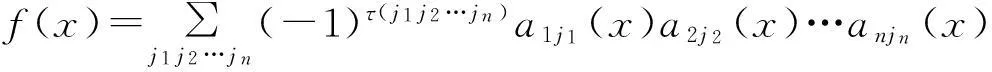
其中j1j2…jn表示123…n的全排列，τ(j1j2…jn)为排列j1j2…jn的逆序数.显然f(x)∈[x]且

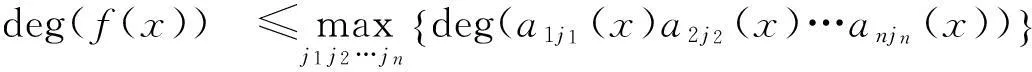
记G*(x)表示多项式矩阵G(x)的伴随矩阵.

引理3伴随矩阵G*(x)是域上的多项式矩阵，且其每个元的次数不超过m(n-1).

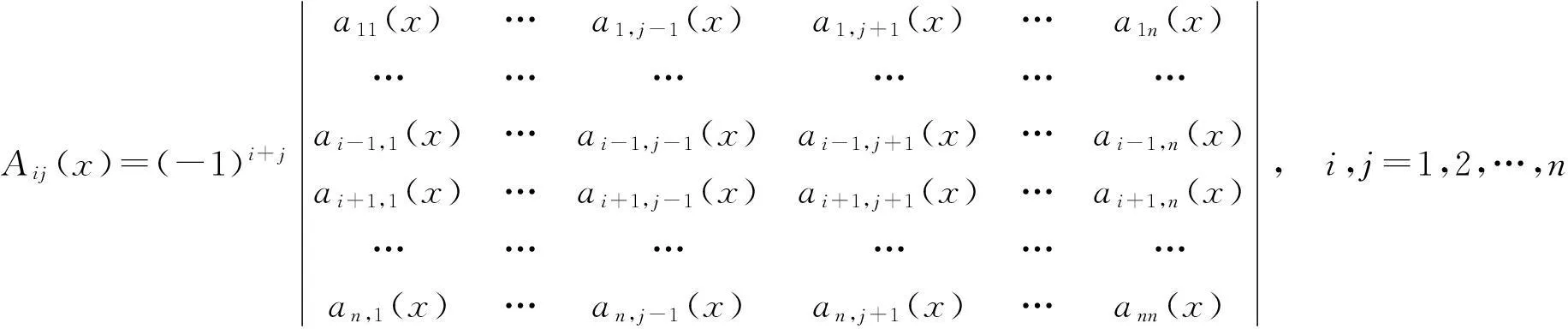
是元为akl(x)的n-1阶行列式，类似引理2的证明知Aij(x)∈[x]且次数不超过m(n-1).

定理设G(x)是一个关于变量x的n阶多项式矩阵， 其每个元的次数不超过m，f(x)=det(G(x)).若存在一个n阶常数方阵A使得G(A)=O，则f(A)=O.

证由引理1，不妨设G(x)=A0+A1x+A2x2+…+Amxm.由引理3不妨设

G*(x)=B0+B1x+B2x2+…+Bm(n-1)xm(n-1).

由引理2，不妨设f(x)=k0+k1x+k2x2+…+kmnxmn∈[x].因为

G*(x)G(x)=det(G(x))E=f(x)E，

其中E为n阶单位矩阵.即

(B0+B1x+B2x2+…+Bm(n-1)xm(n-1))(A0+A1x+A2x2+…+Amxm)

=(k0+k1x+k2x2+…+kmnxmn)E.

比较上面等式两边xk,k=0,1,2,…,mn的系数矩阵，得

k0E=B0A0，

k1E=B0A1+B1A0，

k2E=B0A2+B1A1+B2A0，

k3E=B0A3+B1A2+B2A1+B3A0，

… … … …

kmE=B0Am+B1Am-1+…+Bm-1A1+BmA0，

km+1E=B1Am+B2Am-1+…+BmA1+Bm+1A0，

… … … …

kmn-mE=Bmn-2mAm+Bmn-2m+1Am-1+…+Bmn-m-1A1+Bmn-mA0，

kmn-m+1E=Bmn-2m+1Am+Bmn-2m+2Am-1+…+Bmn-m-1A2+Bmn-mA1，

… … … …

kmn-3E=Bmn-m-3Am+Bmn-m-2Am-1+Bmn-m-1Am-2+Bmn-mAm-3，

kmn-2E=Bmn-m-2Am+Bmn-m-1Am-1+Bmn-mAm-2，

kmn-1E=Bmn-m-1Am+Bmn-mAm-1，

kmnE=Bmn-mAm.

以上各式依次右乘矩阵

E,A,A2,A3,…,Am,Am+1,…,Amn，

然后将所有等式相加，得

k0E+k1A+k2A2+k3A3+…+kmAm+km+1Am+1+…+kmnAmn

=B0A0+(B0A1+B1A0)A+(B0A2+B1A1+B2A1)A2+(B0A3+B1A2+B2A1+B3A0)A3

+…+(B0Am+B1Am-1+…+Bm-1A1+BmA0)Am+(B1Am+B2Am-1+…+BmA1+Bm+1A0)Am+1

+…+(Bmn-2mAm+Bmn-2m+1Am-1+…+Bmn-m-1A1+Bmn-mA0)Amn-m

+(Bmn-2m+1Am+Bmn-2m+2Am-1+…+Bmn-m-1A2+Bmn-mA1)Amn-m+1+…

+(Bmn-m-3Am+Bmn-m-2Am-1+Bmn-m-1Am-2+Bmn-mAm-3)Amn-3

+(Bmn-m-2Am+Bmn-m-1Am-1+Bmn-mAm-2)Amn-2

+(Bmn-m-1Am+Bmn-mAm-1)Amn-1+(Bmn-mAm)Amn，

将上式整理得

f(A)=B0(A0+A1A+A2A2+…+AmAm)+B1(A0+A1A+A2A2+…+AmAm)A

+B2(A0+A1A+A2A2+…+AmAm)A2+B3(A0+A1A+A2A2+…+AmAm)A3

+…+Bmn-m(A0+A1A+A2A2+…+AmAm)Amn-m，

即

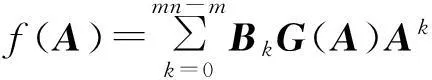
又因为G(A)=O，故f(A)=O.

注2此定理的逆命题不成立，即满足f(A)=O的n阶方阵不一定使G(A)=O.

例取

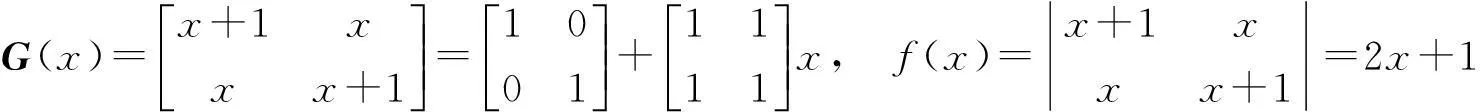
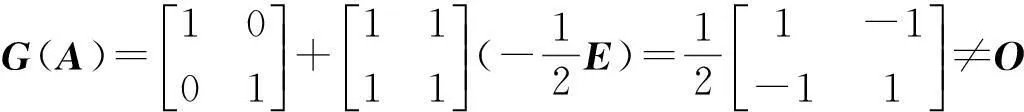
注3经典的哈密尔顿-凯莱定理是此定理的一种特殊情况.对任意方阵A，只需取多项式矩阵为特征矩阵，即取G(x)=xE-A，f(x)=det(xE-A)为A的特征多项式，显然G(A)=O，由定理知f(A)=O.

[参考文献]

[1]北京大学数学系几何与代数教研室前代数小组.高等代数[M].3版.北京:高等教育出版社，2005.

[2]Kaczorek T.Generalization of the Cayley-Hamilton theorem for non-square matrices[J]. International Conference of Fundamentals of Electronics and Circuit Theory XVIIISPETO, Gliwice, 1995: 77-83.

[3]Kaczorek.T. An existence of the Caley-Hamilton theorem for non-square block matrices[J]. Bulletin of the Polish Academy of Sciences, Technical Sciences, 1995, 43(1): 49-56.

[4]Kaczorek.T. An extension of the Cayley-Hamilton theorem for a standard pair of block matrices[J]. Applied Mathematics and Computation Sciences, 1998, 8(3): 511-516.

[5]Wei Xing. Generalization of Cayley-Hamilton theorem for multivariate rational matrices[J].IEEE Transactions on Automatic Control, 2009, 54(3):633-634.

[6]Raj Kumar Kanwar,A generalization of the Cayley-Hamilton theorem[J]. Advances in Pure Mathematics, 2013,3:109-115.

Generalization of Cayley-Hamilton Theorem for Polynomial Matrices

HUJian-hua，WANGZi-Min，ZENGBo-wen

(College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China)

Abstract:Cayley-Hamilton Theorem is a classical conclusion in advanced algebra. It reveals the relationship between the square matrix and its corresponding characteristic polynomial. This paper will generalize the classical Cayley-Hamilton Theorem for polynomial matrix. One relationship between the polynomial matrix and its determinant will be given. So it makes the classical Cayley-Hamilton Theorem a special case of the theorem in this paper.

Key words:Cayley-Hamilton theorem ;polynomial matrices; adjoint matrix

[中图分类号]O151.21

[文献标识码]C

[文章编号]1672-1454(2015)05-0089-04

[基金项目]沪江基金(B14005)；上海理工大学横向项目(1312341001)

[收稿日期]2015-08-02