六点Binary逼近细分法

朱　洪

(安徽三联学院基础部，合肥230601)



六点Binary逼近细分法

朱洪

(安徽三联学院基础部，合肥230601)

[摘要]提出了一种新的细分算法——六点Binary逼近细分法.利用生成多项式等方法对细分法的一致收敛性和Ck连续性进行了分析，通过对细分法中张力参数μ的不同取值，极限曲线可达到C0～C7连续.特别是当μ=11/1024时，极限曲线可达到C9连续.数值算例表明，该方法是合理有效的.

[关键词]Binary细分法； 逼近； 生成多项式； Ck连续性

1引言

细分法是根据初始数据或初始控制多边形由计算机直接生成曲线曲面或其他几何形体的一类方法，其处理方法简单、易于实现，因此在几何造型中得到广泛的应用.Dyn等[1-2]从理论上对Binary细分格式及其极限曲线的存在性和光滑性进行研究，利用三次Lagrange插值提出了四点Binary逼近细分法，可以构造出C2连续曲线.Hassan等[3-4]提出了三点Ternary逼近细分法和四点Ternary插值细分法，并给出了三重格式的充分条件，其生成的极限曲线均达到C2连续.Siddiqi等[5]利用三次均匀B样条基函数构造了一种三点Ternary逼近细分法，并生成了C2连续的极限曲线.Siddiqi等[6-7]提出了五点Binary逼近细分法和五点Ternary逼近细分法，其生成的极限曲线分别达到C3和C4连续.Siddiqi等[8]提出了改进的三点Binary细分算法.Ko等[9]将文献[2]推广到三重格式的情形，提出了四点Ternary逼近细分法.Daniel等[10]将静态格式推广到动态格式，提出了动态的三点Binary逼近细分法，可以产生C1连续的极限曲线.Bao-jun LI等[11]定义了一类带有松弛参数列的动态细分格式，并使得这种方法可以重构指数多项式空间.檀结庆等[12]提出了基于插值细分的逼近细分法，在Hassan四点Ternary插值细分法中引入一个偏移参数，推导出一种逼近细分法，从而使Ternary插值细分和逼近细分统一到一个细分格式中.郑红蝉等[13]介绍了双参数四点细分法及其性质.本文提出了六点Binary逼近细分法，并利用生成多项式方法讨论了极限曲线的收敛性和Ck连续性，使造型曲线具有更大的光滑度，以满足实际应用的需要.

2预备知识

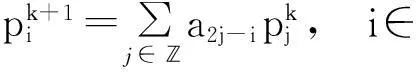
(1)

其中a={ai|i∈}为该细分法的掩模，将细分法记为S，则S的生成多项式为

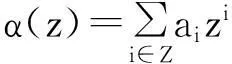
定理1[1]若Binary细分法S一致收敛，则其掩模a={ai}满足

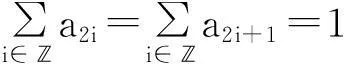
(2)

定理2[1]设Binary细分法S的掩模a={ai}满足式(2)，则存在一个Binary细分法S1，满足

dPk=S1dPk-1,

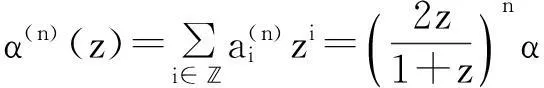
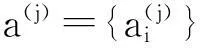
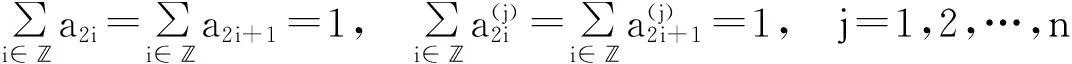
(3)

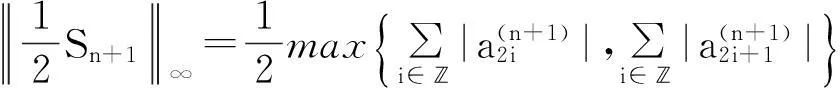
3六点Binary逼近细分法的收敛性和Ck连续性分析

3.1　六点Binary逼近细分法

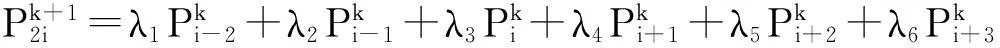
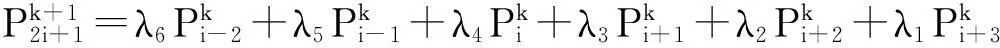
(4)

其中

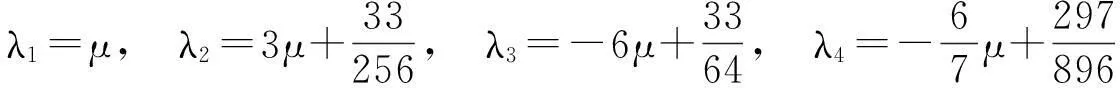
μ为张力参数，且有

λ1+λ2+λ3+λ4+λ5+λ6=1.

3.2　收敛性和Ck连续性分析

证由细分法(4)生成的多项式为

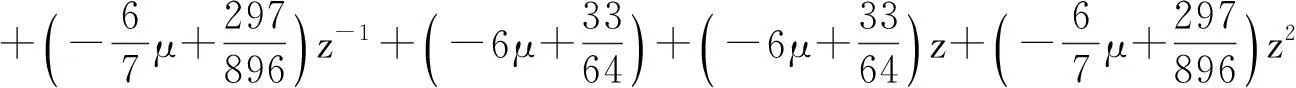
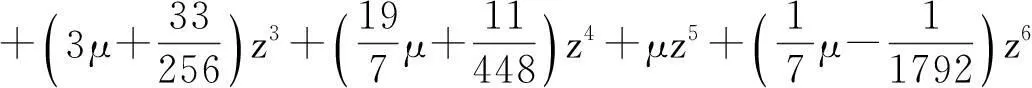
根据定理2知

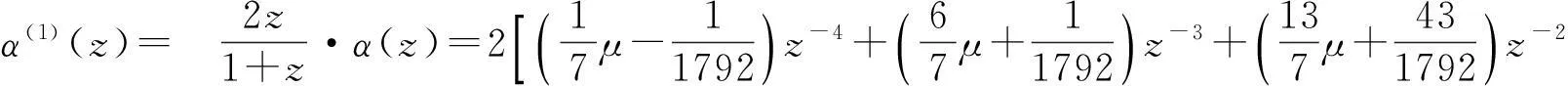
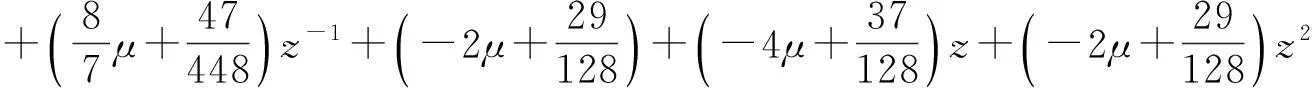
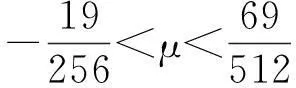
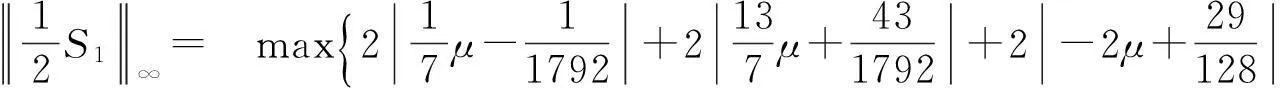
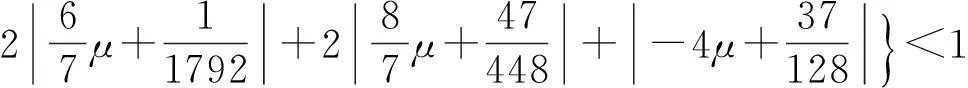
根据定理3知，六点Binary逼近细分法是一致收敛的.

又由定理2知

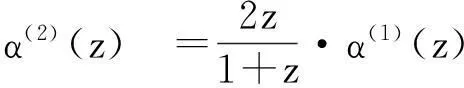
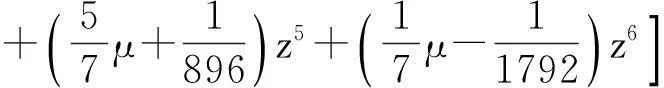
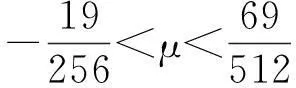
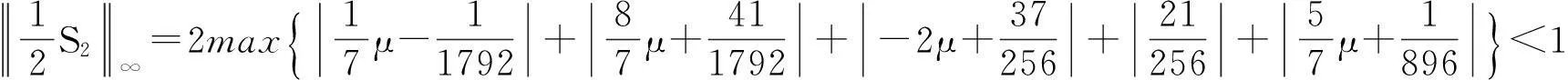
根据定理3知，六点Binary逼近细分法是C1连续的.

证根据定理2知，

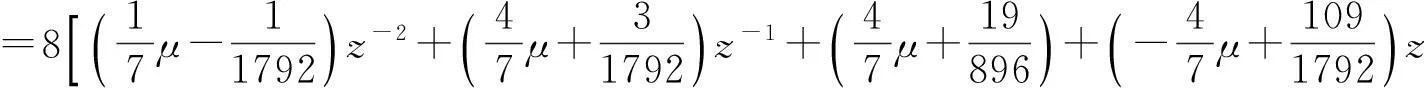
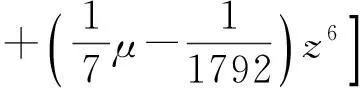
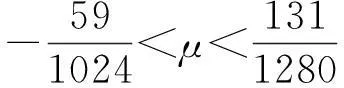
又S4的生成多项式为

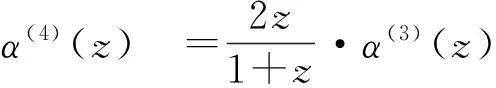
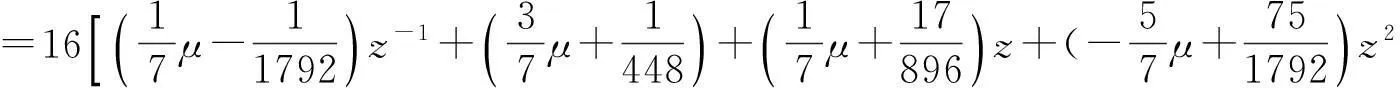
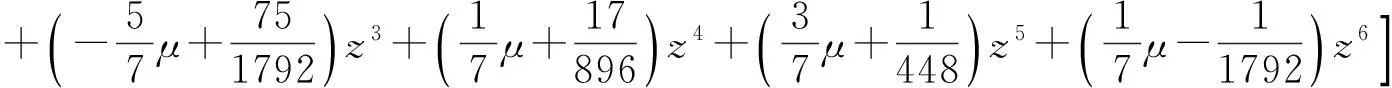
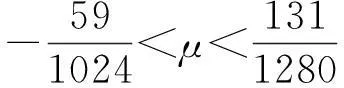
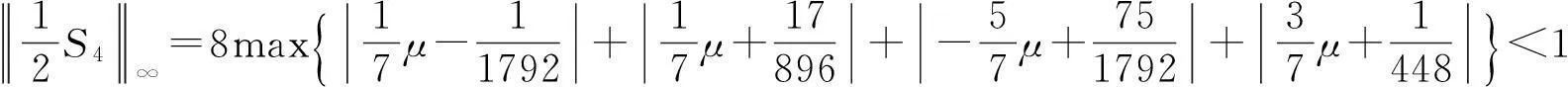
根据定理3知，六点Binary逼近细分法是C3连续的.

证根据定理2知

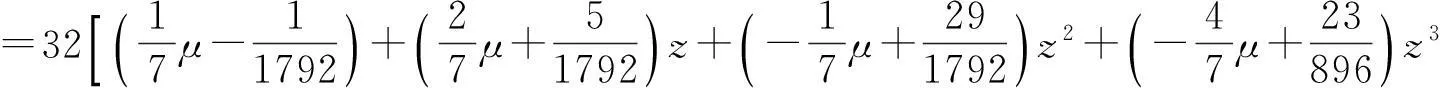
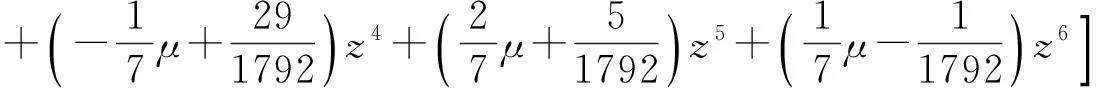
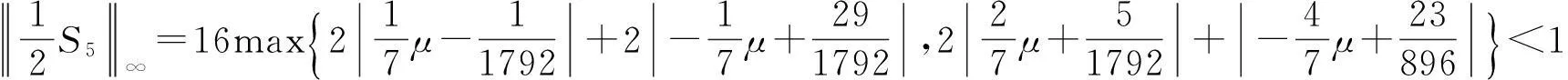
又S6的生成多项式为

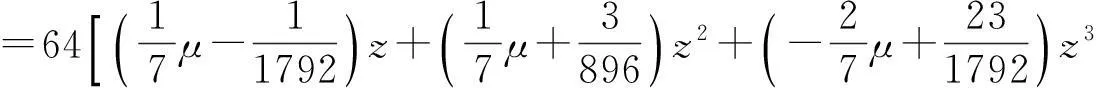
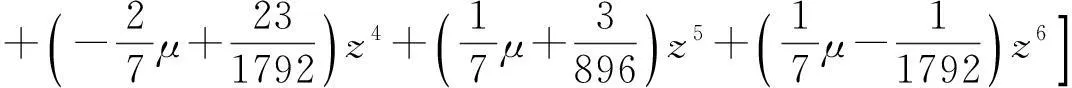
根据定理3知，六点Binary逼近细分法是C5连续的.

证根据定理2知，

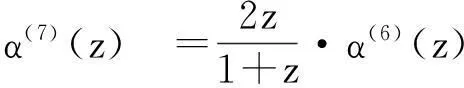
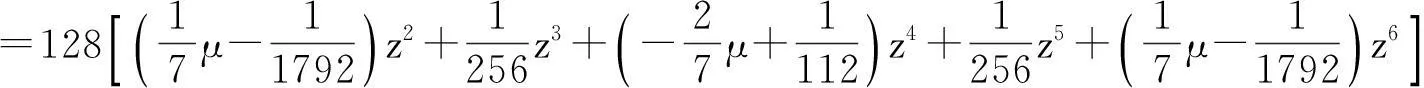
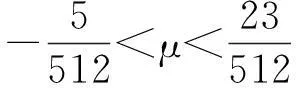
又S8的生成多项式为

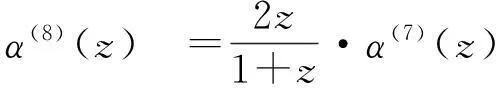
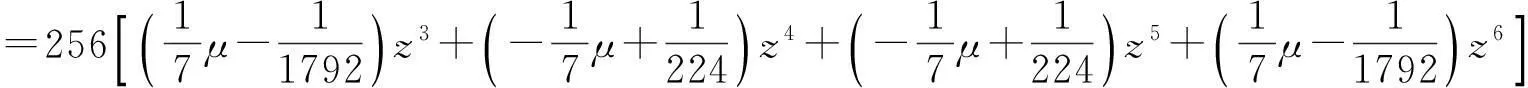
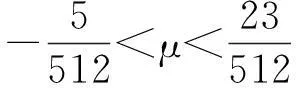
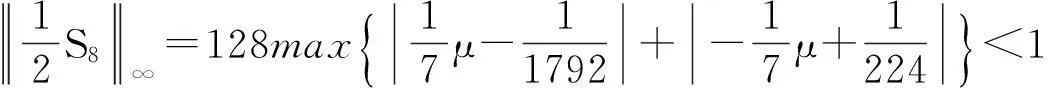
4结论和数值算例

图1　六点Binary逼近细分法算例

[参考文献]图2本文算法与其它几种算法的比较

[1]Dyn N.Subdivision schemes in CAGD[A].Light W (eds.),Advances in Numerical Analysis,Vol.2,Oxford : Clarendon Press,1992:36-104.

[2]Dyn N,Floater M S,Hormann K. A C2four-point subdivision scheme with fourth order accuracy and its extensions[A].Dhlen M,Mørken K,Schumaker L L (eds.),Mathematical Methods for Curves and Surfaces: Tromsø 2004,Nashboro Press,Brentwood,2005:145-156.

[3]Hassan M F,Dodgson N A.Ternary and three-point univariate subdivision schemes[A].Cohen A,Merrien J L,Schumaker L L (eds.),Curve and Surface Fitting:Saint-Malo 2002,Nashboro Press,Brentwood,2003:199-208.

[4]Hassan M F,Ivrissimitzis I P,Dodgson N A,Sabin M A.An interpolating 4-point C2ternary stationary subdivision scheme[J].Computer Aided Geometric Design,2002,19:1-18.

[5]Siddiqi S S,Rehan K.A ternary three-point scheme for curve designing[J].International Journal of Computer Mathematics,2010,87(8):1709-1715.

[6]Siddiqi S S,Ahmad N.A new five-point approximating subdivision scheme[J].International Journal of Computer Mathematics,2008,85(1):65-72.

[7]Siddiqi S S,Rehan K.A stationary ternary C4scheme for curve sketching[J].European Journal of Scientific Research,2009,30(3):380-388.

[8]Siddiqi S S,Rehan K.Modified form of binary and ternary 3-point subdivision schemes[J].Applied Mathematics and Computation,2010,216:970-982.

[9]Ko K P,Lee B G,Yoon G J.A ternary 4-point approximating subdivision scheme[J].Applied Mathematics and Computation,2007,190:1563-1573.

[10]Daniel S,Shunmugaraj P.Three point stationary and non-stationary subdivision scheme[C]∥3rd International Conference on Geometric Modeling & Imaging, London:IEEE Press, 2008:3-8.

[11]Bao-jun LI,Zhi-ling YU,Bo-wen YU,Zhi-xun SU,Xiu-ping LIU.Non-stationary subdivision for Exponential Polynomials Reproduction[J].Acta Mathematicae Application Sinica,2013,29(3):567-578.

[12]檀结庆，童广悦，张莉.基于插值细分的逼近细分法[J].计算机辅助设计与图形学学报，2015,27(7): 1162-1166.

[13]郑红婵,叶正麟,赵红星.双参数四点细分法及其性质[J].计算机辅助设计与图形学学报,2004,16(8): 1140-1145.

A Six-Point Binary Approximating Subdivision Scheme

ZHUHong

(Department of Basic Courses, Anhui Sanlian University, hefei 230009, China)

Abstract:A binary six-point approximating subdivision scheme is presented. Using the generating polynomial method,the uniform convergence and Ck-continuity of subdivision scheme are analyzed. The subdivision scheme can be used to generate a family of Ck(k=1,2,…7) limit curves in certain range of tension parameter μ and C9limit curves forμ=11/1024. The numerical examples show that the proposed method is proper and effective.

Key words:binary subdivision scheme; approximation; generating polynomial; Ck-continuity

[中图分类号]TP391

[文献标识码]C

[文章编号]1672-1454(2015)05-0108-06

[基金项目]安徽三联学院校级自然科学基金(2014Z002)

[收稿日期]2015-07-26