基于Bernstein多项式的二阶线性奇异边值问题的数值解

张卫敏

(合肥工业大学数学学院，合肥230009)



基于Bernstein多项式的二阶线性奇异边值问题的数值解

张卫敏

(合肥工业大学数学学院，合肥230009)

[摘要]提出了一种用Bernstein多项式来构造一类线性奇异两点边值问题的数值解方法.该方法不需要事先对方程进行非奇异化，且若方程的精确解为多项式时，利用这种方法可得方程的精确解.本文包含一些数值实例，并且与三次样条法的数值计算结果进行了比较，从而说明我们提出方法的可靠性和有效性.

[关键词]线性两点奇异边值问题； 数值解； Bernstein多项式

1引言

微分方程奇异边值问题(BVP)在应用数学和物理学领域的应用非常广泛，比如：气体动力学、核物理、化学反应、原子结构、原子计算、非线性椭圆方程正径向解研究等方面.很多问题都会涉及到下面形式的奇异边值问题

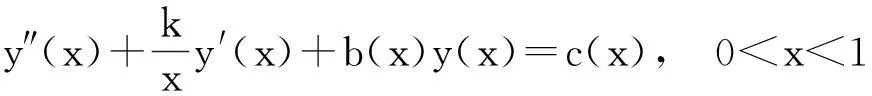
(1)

边界条件

y。′(0)=0和y(1)=β.

很多学者[3，5，6，7]对奇异边值问题都进行了研究.在大多数情况下，使用解析方法很少能得到奇异两点边值问题的解.事实上，我们遇到的很多数学和物理学领域的问题几乎不可能通过解析方法，而是通过各种数值逼近方法来解决.

Albasiny和Hoskins[1]通过求解一组三对角矩阵系数方程得到样条解.Bickely[2]曾考虑使用三次样条方法求解线性两点边值问题.后来，Fyfe[4]通过对Bickley提出的方法进行改善，从而提出线性边值问题新的解决方法.与有限差分方法相比，样条解有它的优势.比如，一旦计算出它的解，那么网格点之间的样条插值的信息是可用的.Ravi Kanth和Reddy[8]讨论了一种基于三次样条函数类的奇异两点边值问题的数值解法.

本文主要利用Bernstein多项式逼近二阶线性微分方程的精确解y(x).如果k/x，b(x)，c(x)都是解析函数，那么方程的解y(x)也是解析函数.根据多项式逼近连续函数的性质，可以用Bernstein多项式逼近二阶线性微分方程的解.

2Bernstein多项式和Weierstrass第一逼近定理

作为经典分析学中经典的理论，用多项式逼近连续函数非常重要.前苏联数学家Korovkin提出了Weierstrass第一逼近定理，该定理给出了多项式逼近连续函数理论的证明.

假设函数f(x)在闭区间[a，b]上有定义，如果存在多项式序列{Pn(x)}在[a，b]上一致收敛于f(x)，则称f(x)在闭区间[a，b]上可以用多项式一致逼近.

应用数学分析语言，多项式一致逼近可等价表述为下面的定理：

定理(Weierstrass 第一逼近定理)设f(x)是闭区间[a，b]上的连续函数，那么，对任意给定的ε>0，总是存在多项式P(x)，使得|P(x)-f(x)|<ε对一切x∈[a，b]成立.

在这里，设区间[a，b]为[0，1]，并且，如果[0，1]上全体连续函数构成的集合为X，全体多项式构成的集合为Y，那么，现在定义映射：

Bn∶X→Y，

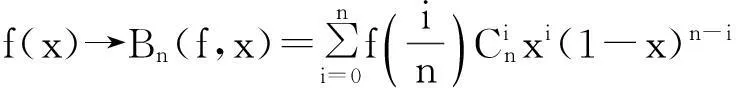
其中Bn(f，x)表示函数f(x)∈X在映射Bn作用下的像，它是以x为变量的n次多项式，称为Bernstein多项式.

3基于Bernstein多项式的数值解法描述

事实上，Bernstein多项式解不一定是问题(1)的精确解y(x)，但是它可以逼近精确解，因此，不妨记(1)的Bernstein多项式近似解为如下形式

(2)

其中Bernstein基函数为

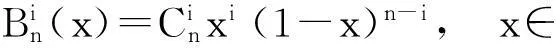
要得到Bernstein多项式，关键就是求出Bernstein系数yi(i=0，1，2，…，n)即可.

因为

和

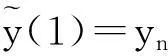
根据问题(1)的边值条件：y′(0)=0和y(1)=β，很明显可以得到

y0=y1和yn=β.

(3)

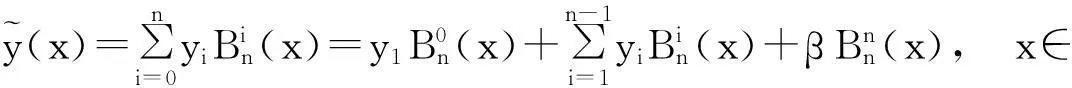
因此，下面只要求出Bernstein系数yi(i=1，2，…，n-1)即可.

对于问题(1)为了使

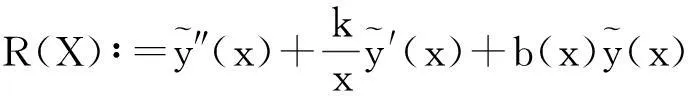
更好的逼近c(x)，利用平方逼近原理，得到

(4)

显然

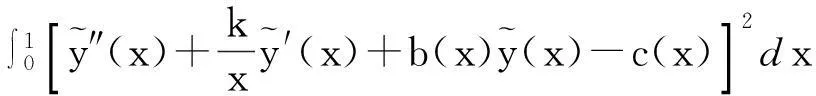
为关于yi(i=1，2，…，n-1)的多元函数，那么上述问题就化为求I=I(y1，y2，…yn-1)的极值问题.

根据多元函数求极限的必要条件，得

(5)

其中

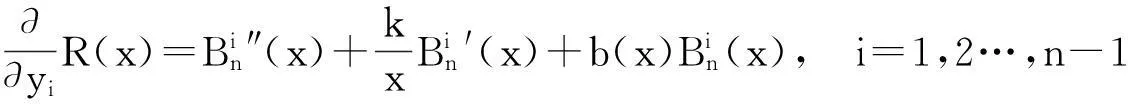
显然，方程(5)是一个由n-1个线性方程构成的含有n-1个未知数yi(i=1，2，…，n-1)的方程组.根据方程组(5)就可以求出yi(i=1，2，…，n-1).

这样，就可以得到线性两点奇异边值问题(1)的Bernstein多项式近似解

其中Bernstein基函数为

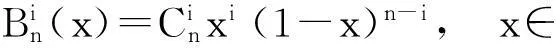
4实例与比较

在本节，通过考虑一些线性两点奇异边值问题的例子，对Bernstein多项式方法加以说明.

例1考虑下面的线性两点奇异边值问题

它的精确解是

.

当N=5，10时，Bernstein多项式数值解已经列示在表1中.通过观察表格中的数据得知，当N=5时，Bernstein多项式近似解就已经可以很好的逼近精确解，当然随着N的越大精确度也会进一步提高；同时，还把Bernstein多项式解与三次样条解进行了比较，比较的结果进一步说明Bernstein多项式数值解法的优越性.

例2考虑下面的线性两点奇异边值问题

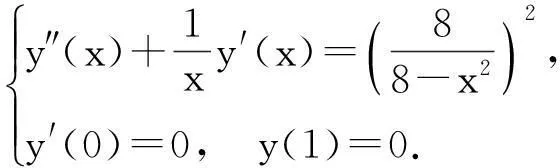
它的精确解是

它的数值解在表2中给出.通过观察得知，提出的方法得到的数值解有很好的精确性.事实上，如果线性两点边值问题的精确解是一个多项式，那么通过Bernstein多项式逼近得到的近似解其实就是它的精确解.

表2　例2数值解与精确解的比较

例3考虑下面的线性两点奇异边值问题

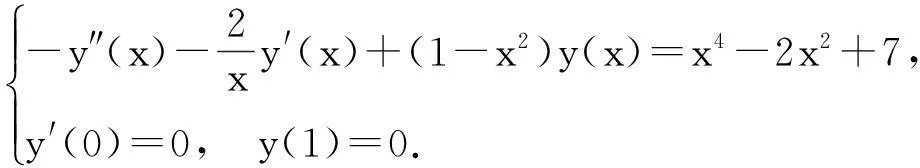
它的精确解是一个多项式

y(x)=1-x2.

计算结果已经在下面的表3中给出.因为该线性两点边值问题的解是多项式，那么就可以用Bernstein多项式直接得到精确解.

表3　例3数值解与精确解的比较

5总结与展望

微分方程线性两点奇异边值问题在应用数学和物理学领域的应用非常广泛.本文的重点是以Bernstein多项式为工具，利用多项式逼近连续函数的性质，来求二阶线性奇异边值问题的数值解.所采用的方法具有如下优点：首先，不需要对微分方程事先做非奇异化处理，其次，若方程的解析解是多项式，用该方法可得到方程的解析解而不仅仅是近似解.本文中，还给出了一些数值实例把所提出的方法得到的数值结果与其他已有方法得到的数值结果进行比较，从而得到解决此类问题的各种方法的优缺点.

本文所提出的微分方程数值解法虽然在实际应用中具有良好的效果，但也存在着一些待解决的问题和未完成的工作.随着微分方程数值解的不断发展，在应用数学和物理学领域遇到的问题越来越多，这就要求我们不仅仅要解决线性问题，还有研究非线性问题.Bernstein多项式在求解线性两点奇异边值问题方面体现了它的优越性，那它在解决非线性两点奇异边值问题方面是否仍旧保持这种特性，这将是我们以后将要继续探究的问题.

[参考文献]

[1]Albasiny E L， Hoskins W D. Cubic splines solutions to two-point boundary value problems [J]. Comput. J， 1969， 12 (2):151-153.

[2]Bickley W G. Piecewise cubic interpolation and two point boundary value problems [J]. Comput .J， 1968， 11(2) : 206-212.

[3]Chawla M M， Katti C P. A finite difference method for a class of singular two point boundary value problems [J]. IMA. J. Numer. Anal， 2008，36(4): 457-466.

[4]Fyfe D J. The use of cubic splines in the solution of two-point boundary value problems [J]. Comput. J， 1969， 12(2): 188-192.

[5]Gustafsson B. A numerical method for solving singular boundary value problems [J].Numer. Math， 1973， 21(4): 328-344.

[6]Jamet P. On the convergence of finite difference approximations to one dimensional singular boundary value problems [J]. Numer. Math， 1970， 14 (4):355-378.

[7]Ravi Kanth A S V， Reddy Y N. A numerical method for singular boundary value problems via Chebyshev economization [J].Appl. Math. Comput， 2003 ，146 (3) : 691-700.

[8]Ravi Kanth A S V， Reddy Y N. Cubic spline for a class of singular two-point boundary value problems [J].Applied Mathematics and Computation，2006， 170(2):733-740.

Numerical Solution for Linear Singular Two-point Boundary

Value Problems Based on Bernstein Polynomials

ZHANGWei-min

(School of Mathematics， Hefei University of Technology， Hefei 230009， China)

Abstract:We present a figure based on Bernstein polynomials in compression for a class of singular two-point boundary value problems. This method does not require non-singularity of the equation， and if the exact solution is a polynomial solution， we can get the exact solution by using this method. Some examples have been included and comparison of the numerical results made with cubic spline method. Then the reliability and efficiency of the proposed method are demonstrated by several examples.

Key words:the linear singular two point boundary value problem; the numerical solution; Bernstein polynomials

[中图分类号]O141.81

[文献标识码]C

[文章编号]1672-1454(2015)05-0093-05

[收稿日期]2015-03-26