一元五次B样条拟插值研究
钱 江,王永杰
(河海大学 理学院,江苏 南京 211100)
引言
样条函数是一种分段或分片光滑,且在各分段分片的交界处都具有一定光滑性的函数,其相关研究始于20世纪中叶,数学家I.J.Schoenberg在1946年首次提出一元样条理论[1]。随着样条理论的不断发展,内容丰富、应用广泛的样条方法已经成为了研究数值逼近的有力工具。样条函数[2-5]因为其光滑性、保凸性、保多项式性等特点,常常在有限元、计算机辅助几何设计、微分方程数值解等领域取得非常优秀的效果,且应用广泛。

考虑到更高次的样条函数在逼近理论中应具有更高的精度[18-19],而计算高次的B样条需要较复杂的方法与技巧,由此将高次样条函数应用于微分方程数值解值得进一步研究。同时,在比较五次B样条微分正交法[20]时发现,文献[20]仅仅给出无重节点情况下的五次B样条函数,且该函数并不具有单位分解性。鉴于此,本文将在已经计算出五次B样条基函数基础上,对样条拟插值及其应用进一步开展研究。
本文首先回顾一元五次B样条基函数,给出数值算例,绘制图形;然后建立五次样条拟插值算子;接着针对具有不同光滑度的被逼函数,分析样条拟插值的误差估计;最后将五次样条应用于求解抛物型方程,并与四次B样条方法作比较。
1 五次B样条基函数的回顾
我们已经利用光滑余因子协调法分别计算出区间[x0,xn]上具有均匀节点{xi,xi+1,xi+2,xi+3,xi+4,xi+5,xi+6}与端点x0,xn处具有有重节点的一元五次B样条基函数。为避免赘述,本节将通过具体数值算例回顾五次B样条基函数[21]。
算例1令x0=0,x5=5,xi+1-xi=1,i=0,1,2,3,4,分别得到子区间[x0,x1],[x1,x2],[x2,x3],[x3,x4],[x4,x5]上带有重节点的五次B样条基函数。例如在区间[x0,x1]上,B样条基函数具有如下表达式

(1)
由B样条基函数的单位分解性知

(2)

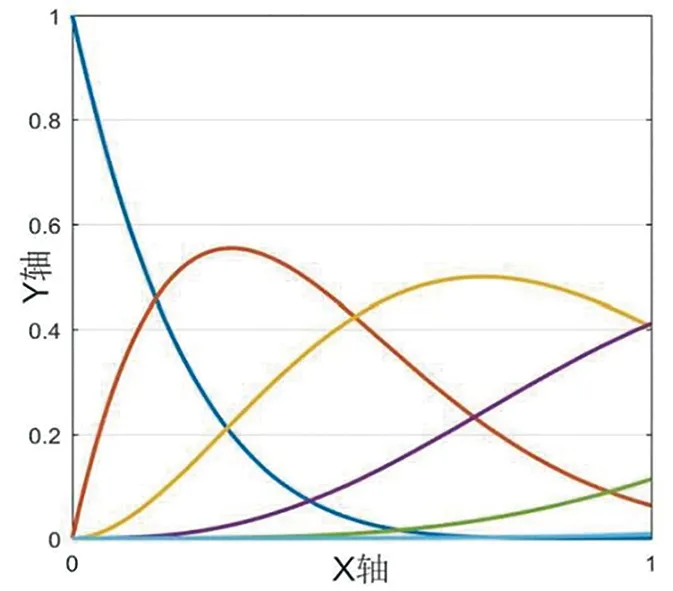
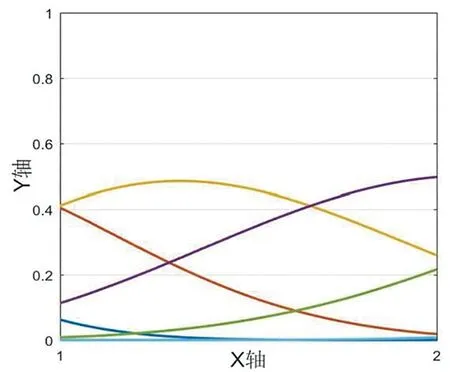
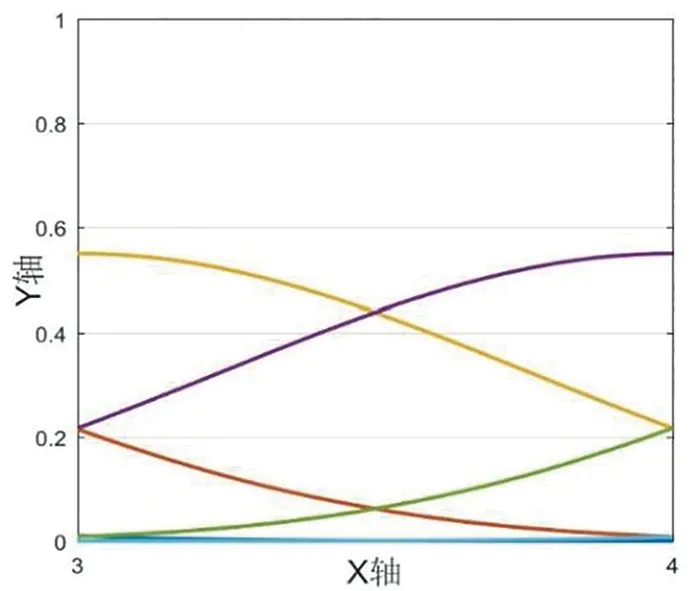
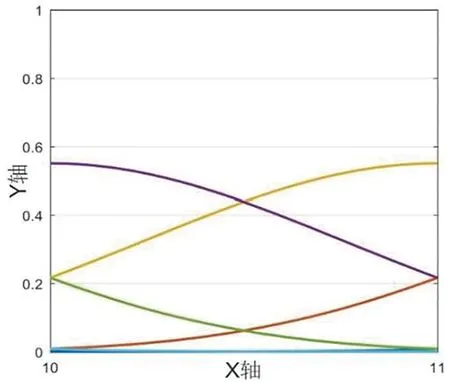
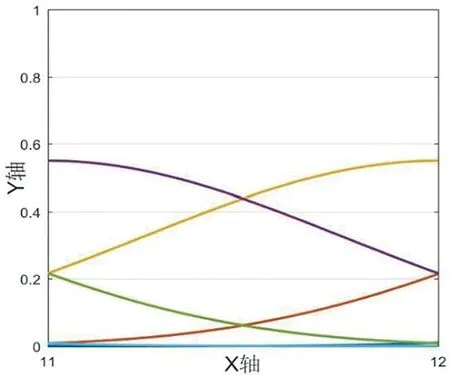
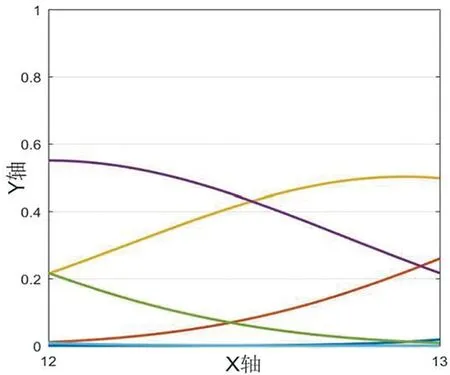
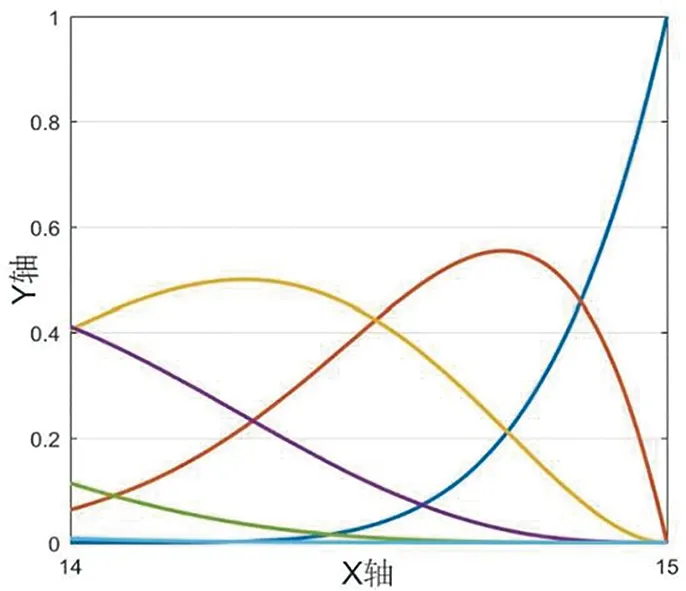
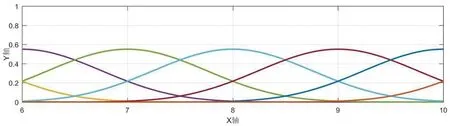
我们绘制图形,如图1-5所示,其中X轴表示区间节点,Y轴表示函数曲线在该节点出的值,下文若没有特殊说明,则与其一致。
类似于对左端点处带有重节点的五次B样条的分析,同样可以得到右端点处带有重节点的五次B样条基函数。
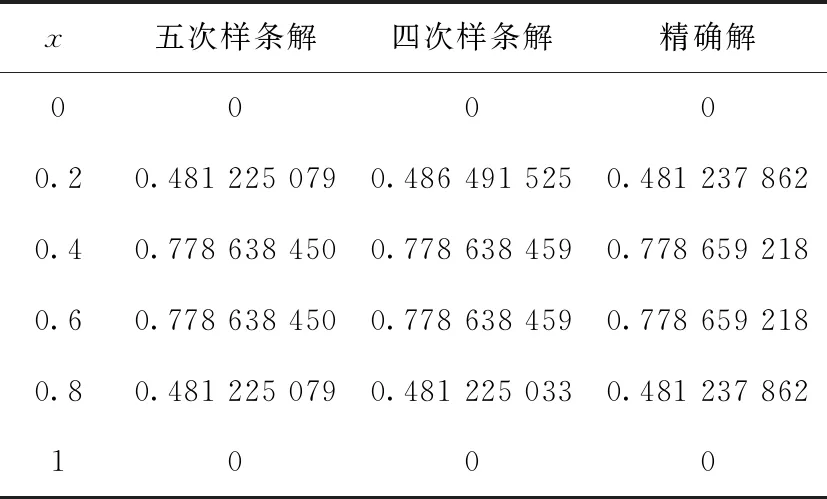
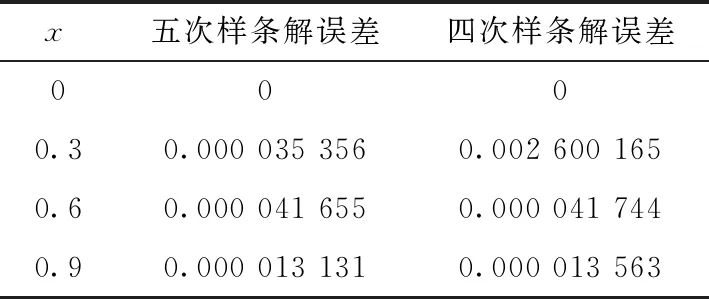
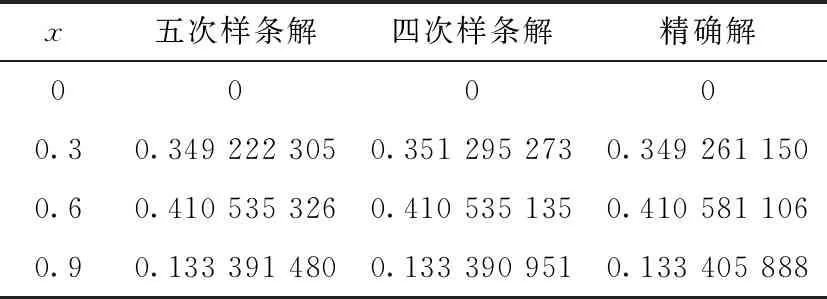
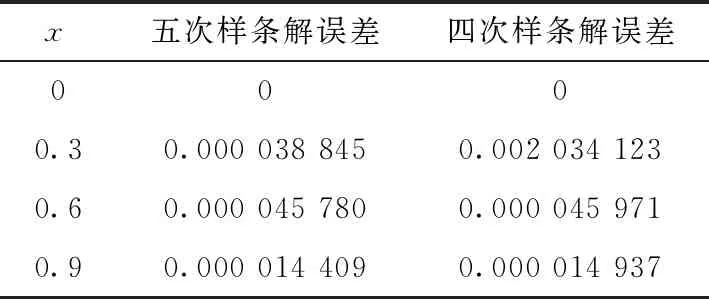
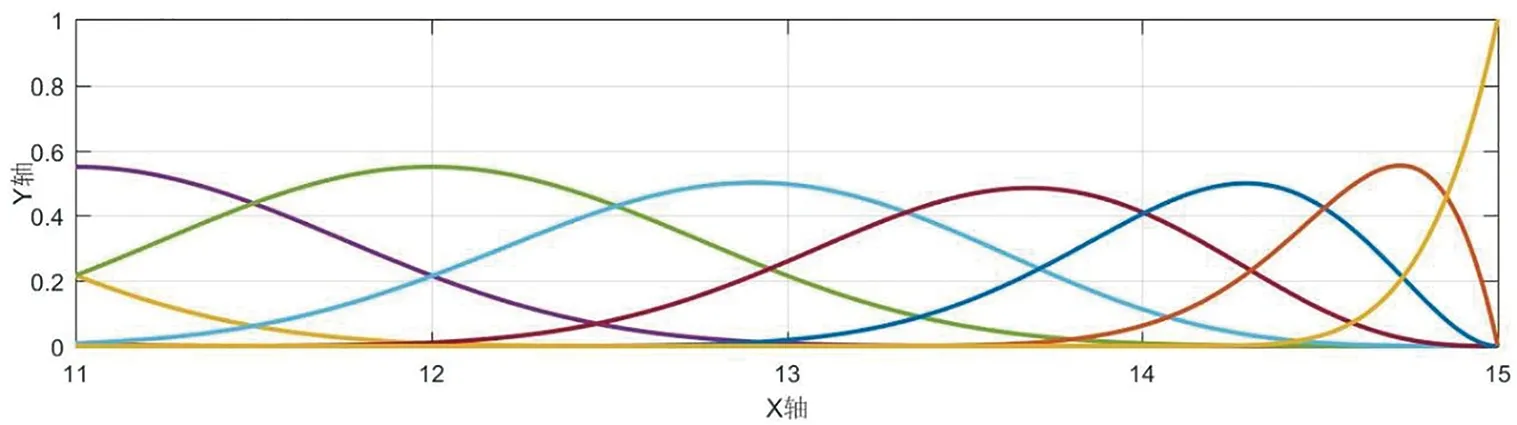
算例2当xn-5 (3) 由B样条基函数的单位分解性知 (4) 绘制图形,如图6-10所示。 为了更好地认识五次B样条基函数,我们给出在有界闭区间[x0,xn]上五次B样条函数图像的左半部分[x0,x4]区间、中间部分[xi,xi+4]区间(均匀节点)、右半部分[xn-4,xn]区间,其中x0=0,xn=15,xi+1-xi=1,i=0,1,…,n,如图11-13所示。 图1 I0=[x0,x1]上的五次B样条基函数 图2 I1=[x1,x2]上的五次B样条基函数 图3 I2=[x2,x3]上的五次B样条基函数 图4 I3=[x3,x4]上的五次B样条基函数 图5 I4=[x4,x5]上五次B样条基函数 图6 In-5=[xn-5,xn-4]上五次B样条基函数 图7 In-4=[xn-4,xn-3]上五次B样条基函数 图8 In-3=[xn-3,xn-2]上五次B样条基函数 图9 In-2=[xn-2,xn-1]上五次B样条基函数 图10 In-1=[xn-1,xn]上五次B样条基函数 图11 区间[x0,x4]上的五次B样条函数 图12 区间[xi,xi+4]上均匀节点下的五次B样条函数 图13 区间[xn-4,xn]上的五次B样条函数 本节将构造保五次多项式性的线性泛函,即五次B样条拟插值算子。 定理1设fi=f(xi),i=0,1,…,n,其中xi-xi-1=h,i=1,2,…,n,且节点x-5=x-4=x-3=x-2=x-1=x0 Wn(f)≡f,∀f∈P5 , (5) 其在每个区间中的拟插值表示分别为 (6) (7) (8) (9) (10) (11) 其中,x∈[xi,xi+1],i=5,6,…n-6。 对称地,我们可以算出子区间[xn-5,xn-4],[xn-4,xn-3],[xn-3,xn-2],[xn-2,xn-1]及[xn-1,xn]上的五次B样条拟插值算子。 本节我们将利用连续模与Taylor公式对五次B样条拟插值进行相应的误差估计。首先给出连续模与极大范数的定义: wI(f,r):=sup {|f(x)-f(u)|:x,u∈I,|x-u|≤r} , (12) (13) 其中,I=[x0,xn],xi+1-xi=h,i=0,1,…,n-1。 针对具有不同光滑度的函数,我们给出如下样条拟插值的误差分析。 定理2设f(x)∈C(I),则对充分大的正整数n,Wn(f)的误差估计满足 (14) (15) 证明:利用五次B样条基函数的单位分解性,我们可以得出 f-Wn(f)=f(x)(si-5(Ii)+si-4(Ii)+si-3(Ii)+si-2(Ii)+si-1(Ii)+si(Ii))-Wn(f)。 从而有 ‖f-Wn(f)‖Ii=‖f(x)(si-5(Ii)+si-4(Ii)+si-3(Ii)+si-2(Ii)+si-1(Ii)+si(Ii))-Wn(f)‖Ii 当x∈I0=[x0,x1]时,有 同理可以验证x∈I1,I2,I3,I4,In-5,In-4,In-3,In-2,In-1的情况。 定理3令f(x)∈C1(I),则对充分大的正整数n,Wn(f)的误差估计满足 (16) (17) 事实上,令f(x)∈C1(I),当x∈Ii=[xi,xi+1]时,将f(x)在区间中点xi+1/2处展开,我们得到 f(x)=T1,i(x)+(f′(ξi)-f′(xi+1/2))(x-xi+1/2)⟹f(x)-T1,i(x)=(f′(ξi)-f′(xi+1/2))(x-xi+1/2), 其中T1,i(x)=f(xi+1/2)+f′(xi+1/2)(x-xi+1/2)。 类似地,我们利用连续模与Taylor公式得到如下定理。 定理4令f(x)∈C2(I),则对充分大的正整数n,Wn(f)的误差估计满足 (18) (19) 定理5令f(x)∈C3(I),则对充分大的正整数n,Wn(f)的误差估计满足 (20) (21) 定理6令f(x)∈C4(I),则对充分大的正整数n,Wn(f)的误差估计满足 (22) (23) 本节我们考虑抛物型方程: (24) 初边值为 u(x,0)=sin (πx),u(0,t)=u(1,t)=0, 精确解为 u(x,t)=e-tsin (πx)。 对方程(24)在点(xi,tk)按时间步长τ进行离散,引入参数δ(0≤δ≤1),我们得到 (25) (26) 接下来,我们利用均匀节点下的五次B样条基函数来逼近该抛物型方程。令时间步长为τ=0.04,空间步长为h=0.02,δ=0.5。在下列表格中,我们分别取t=0.2,t=0.6和t=0.84,且对x取不同值与精确解作对比。 从上述表格中可以看出,我们用五次B样条逼近得到的解准确率高,而且得到的解与精确解的误差远小于比它低一次的四次B样条解误差,逼近效果更好。在迭代过程中,我们发现,用四次样条迭代得到的数据是波动的,而用五次样条迭代出的数据更加的顺滑稳定。用抛物型方程举例,虽然常用三次样条逼近,但在相同步长的情况下,在相同的有限闭区间上需要更少的五次B样条,取得更好的逼近效果。 本文在一元五次B样条的基础上,给出了一元五次B样条拟插值,再根据函数的光滑度不同,利用Taylor公式进行相应的误差估计,并尝试运用在求解逼近方程中。在以后的工作中,作者将利用本文构造的五次B样条拟插值算子求解其他类型的方程,并拟给出张量积型双五次B样条基函数以及其在微分方程数值解方向上的应用。 表1 t=0.2时五次样条解、四次样条解与精确解对比 表2 t=0.2时两种样条解与精确解的数值误差对比 表3 t=0.6时五次样条解、四次样条解与精确解对比 表4 t=0.6时两种样条解与精确解的数值误差对比 表5 t=0.84时五次样条解、四次样条解与精确解对比 表6 t=0.84时两种样条解与精确解的数值误差对比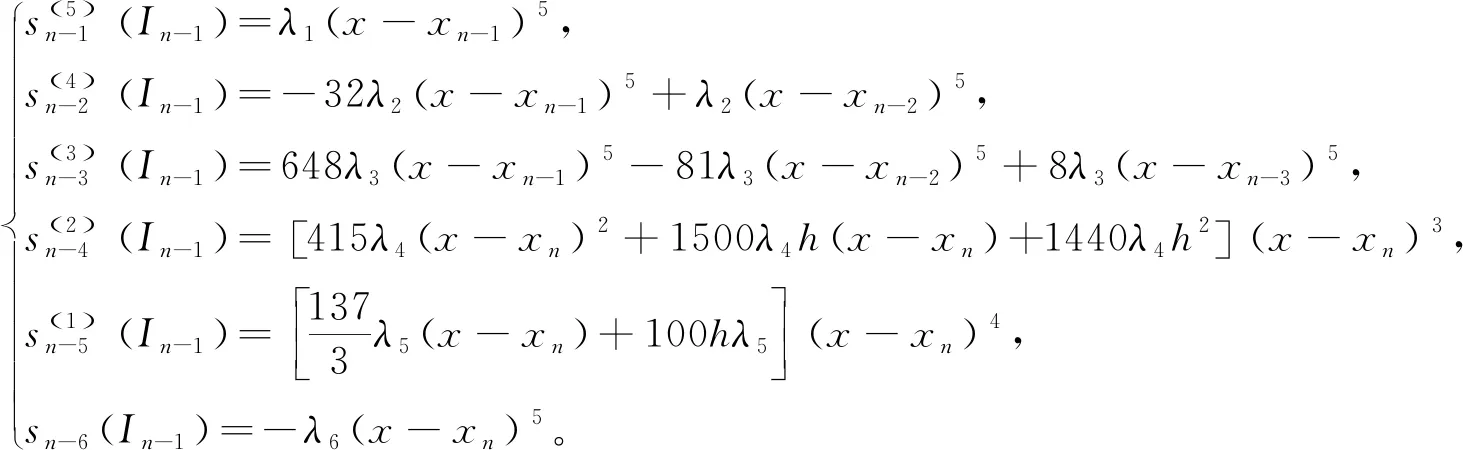






2 五次B样条拟插值算子
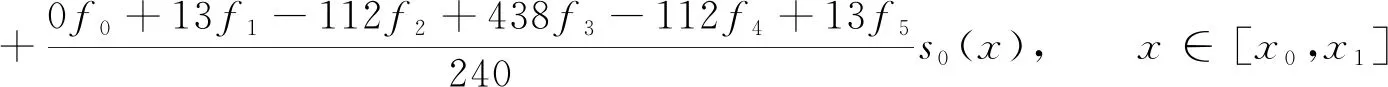
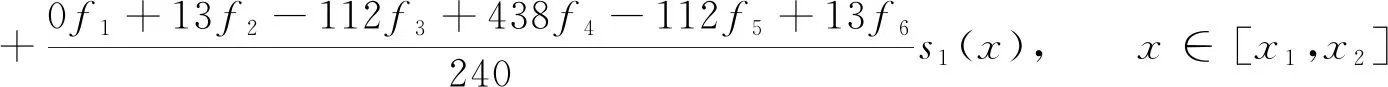
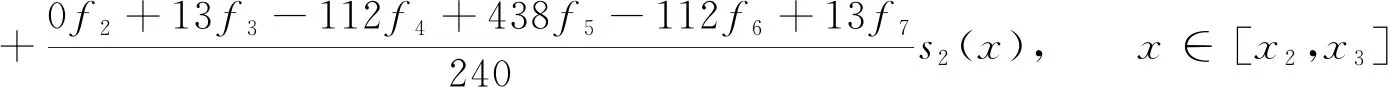



3 样条拟插值的误差估计



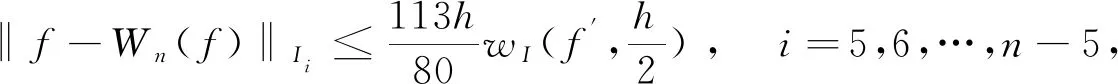
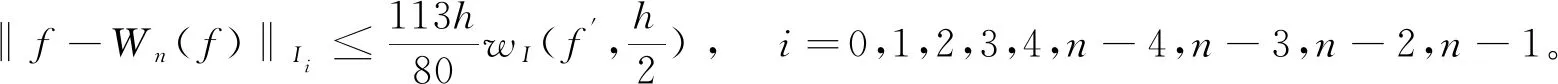
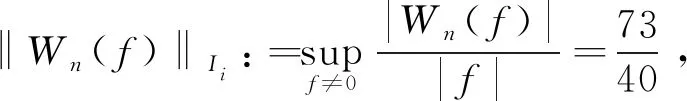

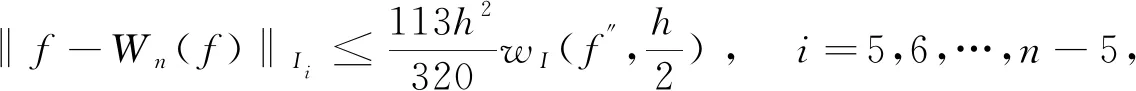
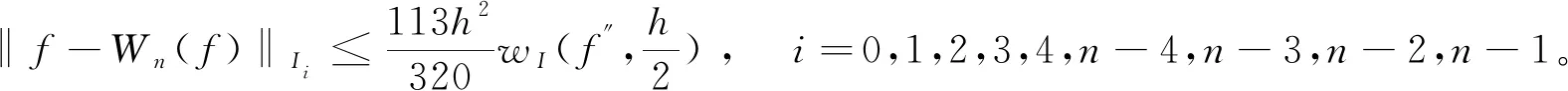
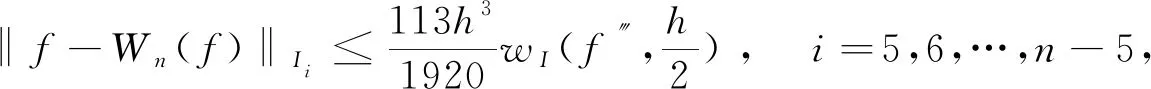
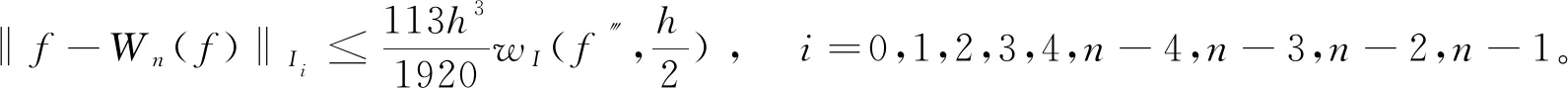
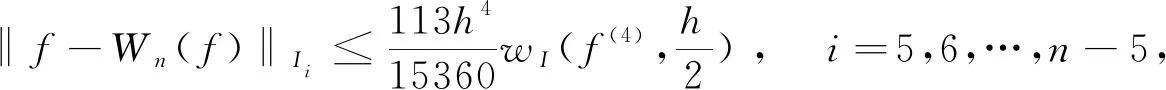

4 数值算例
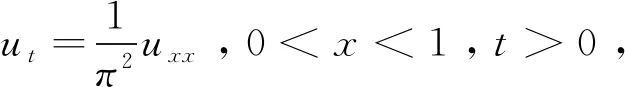

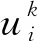

5 结语