一道数学竞赛题的多种解法
2016-01-28 03:07:04周玲,孙琳
大学数学 2015年5期
周 玲, 孙 琳
(合肥工业大学数学学院,合肥230009)
一道数学竞赛题的多种解法
周玲,孙琳
(合肥工业大学数学学院,合肥230009)
[摘要]给出了北京市第一届大学生数学竞赛一道试题的多种解法.
[关键词]数列极限; 夹迫原则; 递推方法; 压缩映象原理; 矩阵方法; 级数方法
北京市第一届大学生数学竞赛试题的第三题[1]是

文[1]给出的解法是,先假定该数列的极限存在并求出其值,然后利用数列极限的定义予以证明. 本文将给出该试题的另外解法,仅供大家教学中作为参考.
1利用数列的通项公式直接求极限
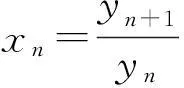

从而
yn+2-2yn+1-yn=0.
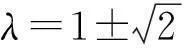
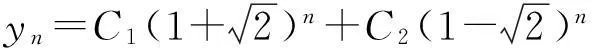
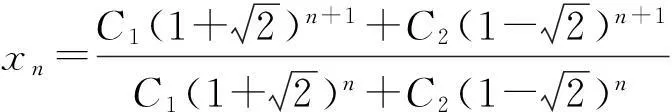
(1)
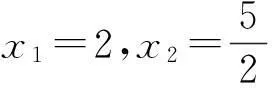

2利用判别数列极限存在的夹迫原则
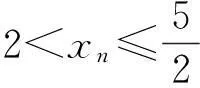
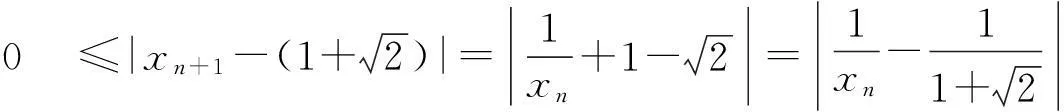

所以
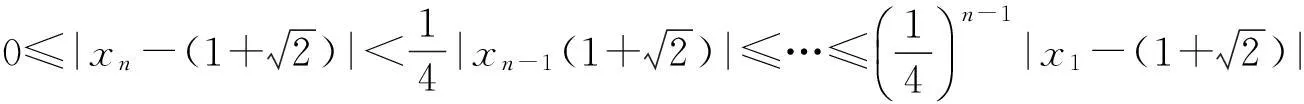
3利用关于xn的递推式
先介绍如下的
命题1设数列{xn}满足线性有理递推关系

(2)
若λ和μ是方程cr2+(d-a)r-b=0的两个不相等的实根,则
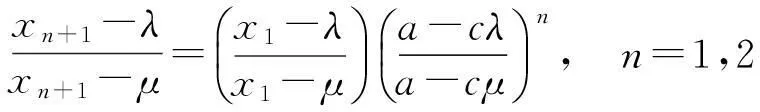
(3)
这是因为
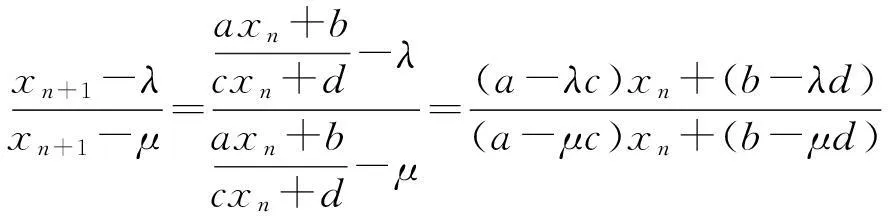
注意到cλ2+(d-a)λ-b=0及cμ2+(d-a)μ-b=0,故上式可写成

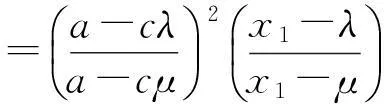
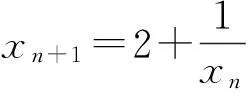
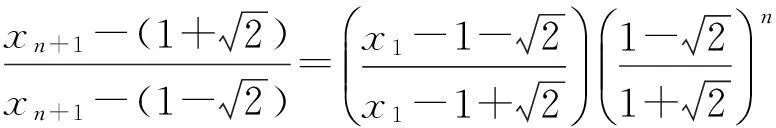
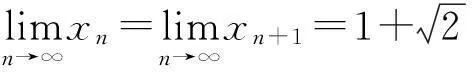
4利用压缩映象原理
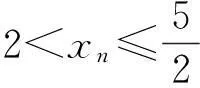
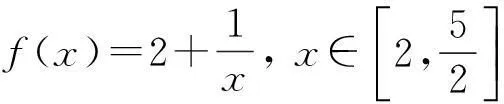
易知

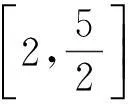
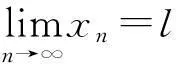
5矩阵方法
用数学归纳法不难证明(过程从略)如下的
命题2设数列{xn}满足线性有理递推关系式(2),若令
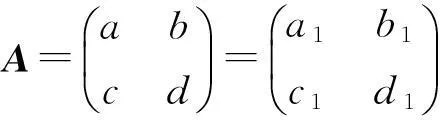
(4)

(5)
则
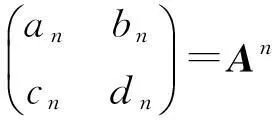
(6)
A的特征方程为
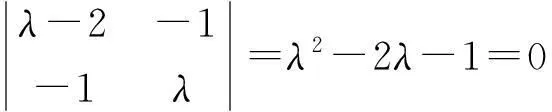

令
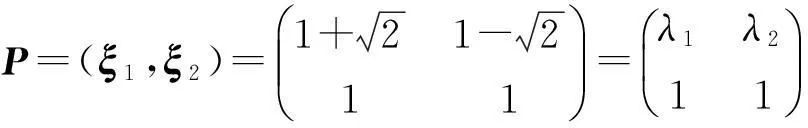
则有
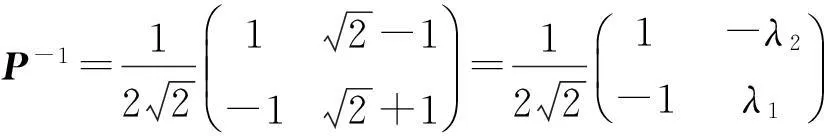
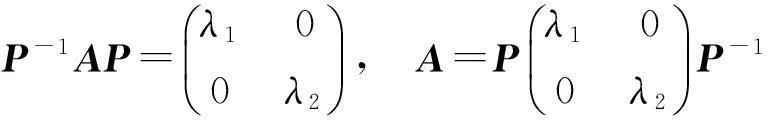
从而

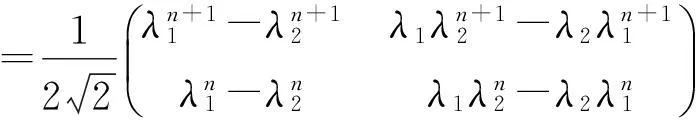
由(5),(6),故有

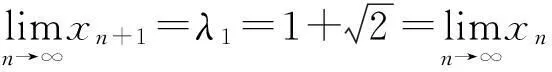
6级数方法
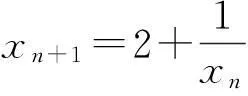
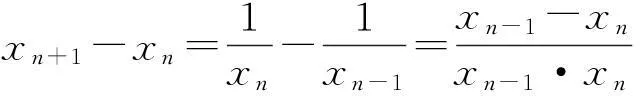
故
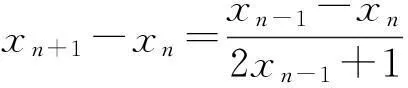
由题设易知xn>2 (n=1,2,…),从而

由级数收敛的定义,有


[参考文献]
[1]李心灿,季文铎,孙洪祥,等.大学生数学竞赛试题解析选编[M].北京:机械工业出版社,2011.
[中图分类号]O13;O151.2
[文献标识码]C
[文章编号]1672-1454(2015)05-0104-04
[基金项目]合肥工业大学教学改革研究项目(YJG2012Y12)
[收稿日期]2014-09-10

