多元函数条件极值的必要条件
张冬燕, 王耀革, 张武军
(解放军信息工程大学理学院,郑州450000)
多元函数条件极值的必要条件
张冬燕,王耀革,张武军
(解放军信息工程大学理学院,郑州450000)
[摘要]推导证明了一般n元函数及常用的二元、三元函数在等式约束条件下用行列式表示的极值的必要条件,并从几何上对二元、三元函数在等式约束条件下取极值的必要条件予以了直观解释.利用这些必要条件求解条件极值,因除去了Lagrange乘数法带来的Lagrange乘子对解方程组的困扰,而使得最终方程组的求解变得明快简洁.
[关键词]多元函数; 条件极值; 必要条件
1引言
构造Lagrange函数,在Lagrange函数驻点中寻找目标函数在等式约束条件下可能的极值点,Lagrange乘数法因着清晰流畅的求解思路成为求解条件极值问题的一把利器. 但是,因为在求解Lagrange函数驻点过程中产生了由各样方程构成的方程组,方程组的求解成了一个难点. 文献[1-2]借助线性方程组理论给出了利用行列式简化求解二元、三元函数条件极值的方法,这种方法因减少了Lagrange乘子的干扰而使求解最终方程组变得简单,能否将此方法推广到求解一般n元函数在多个约束条件下的条件极值呢?在此思想的启发下,我们尝试探讨了一般n元函数在等式约束条件下用行列式表示的极值的必要条件.
2主要结论
1.1 函数u=f(x1,x2,…,xn)在k定理1.1设
f(x1,x2,…,xn),φi(x1,x2,…,xn),i=1,2,…,k
均具有一阶连续偏导数,φi(x1,x2,…,xn), i=1,2,…,k对各个变量的偏导数不全为零,且

线性无关,则u=f(x1,x2,…,xn)在条件
φi(x1,x2,…,xn)=0,i=1,2,…,k
下以点P0为极值点的必要条件是
φi(P0)=0,i=1,2,…,k
且在该点处矩阵

的任意n-k个k+1级子式等于零.
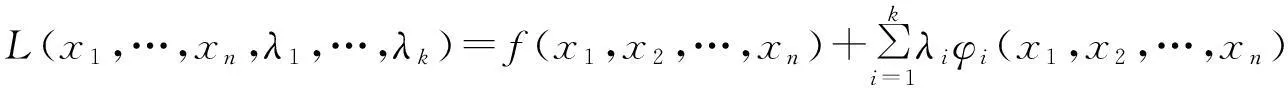
由文[3]知,在定理条件下u=f(x1,x2,…,xn)在P0处取极值的必要条件是在该点处满足

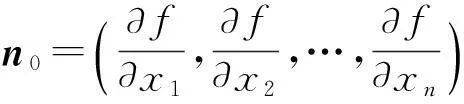
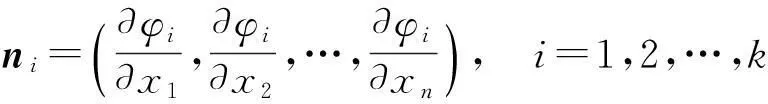
分别是f(x1,x2,…,xn)=c和φi(x1,x2,…,xn)=0的法向量.下面依然寻找可简化方程组(1)的行列式.注意到方程组(1)用向量ni,i=0,1,2,…,k可表示为
n0=-(λ1n1+λ2n2+…λknk),
其中n1,n2,…,nk线性无关,也就是说n0,n1,n2,…,nk线性相关,且它们的秩等于k,于是以n0,n1,n2,…,nk为行向量的矩阵

的秩为k.而由代数学知识,矩阵秩为k的充要条件是矩阵所有k+1级子式等于零[4].这里我们要找的是方程组(1)中变量x1,x2,…,xn需满足的等式,因此只需任取其中n-k个k+1级子式,即和方程组(2)共同构成了极值点P0的坐标需满足的等式.
显然,若定理中n=3,三元函数u=f(x,y,z)在条件φ(x,y,z)=0下取得极值的必要条件就是:
推论1.1设f(x,y,z),φ(x,y,z)具有一阶连续偏导数,且φz(x,y,z)≠0(或φx,φy不全为零),则u=f(x,y,z)在条件φ(x,y,z)=0下以点P0(x0,y0,z0)为极值点的必要条件是在该点满足

证u=f(x,y,z)在约束条件下以点P0(x0,y0,z0)为条件极值点的必要条件是在该点满足
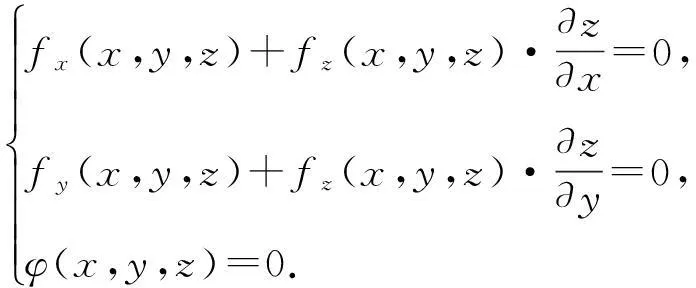
(3)
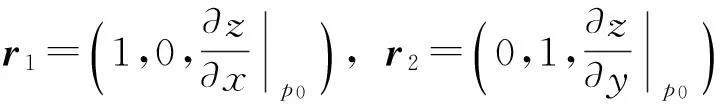
n=(fx(x0,y0,z0),fy(x0,y0,z0),fz(x0,y0,z0)),
则方程组(3)的前两个条件表明n⊥r1,n⊥r2,也就是说在极值点P0(x0,y0,z0)处目标函数的等值曲面f(x,y,z)=c与曲面Σ:φ(x,y,z)=0有公共切平面,等值曲面与曲面Σ在P0(x0,y0,z0)处的法向量共线,即在极值点处必有n∥r1×r2,又
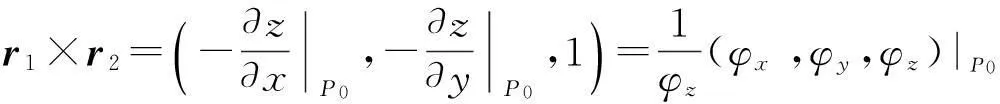
从而在P0(x0,y0,z0)处有
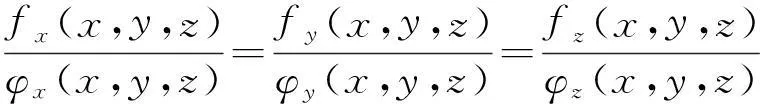
用行列式表示即得所证结论.
1.2 函数u=f(x1,x2,…,xn)在n-1个条件φi(x1,x2,…,xn)=0,i=1,2,…,n-1下的极值
定理1.2设
f(x1,x2,…,xn),φi(x1,x2,…,xn),i=1,2,…,n-1
均具有一阶连续偏导数,φi(x1,x2,…,xn),i=1,2,…,n-1对各个变量的偏导数不全为零,且
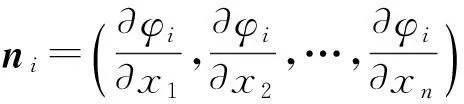
线性无关,则u=f(x1,x2,…,xn)在φi(x1,x2,…,xn),i=1,2,…,n-1以点P0为极值点的必要条件是在该点处满足
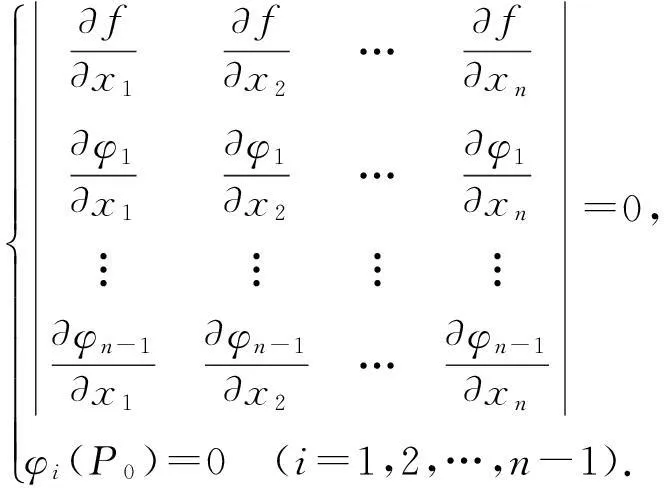
证令

由文[5],已知条件下u=f(x1,x2,…,xn)在φi(x1,x2,…,xn),i=1,2,…,n-1下在点P0处取得极值的必要条件是在该点满足

记f(x1,x2,…,xn)=c的法向量

则方程组(4)可表示为
n0=-(λ1n1+λ2n2+…λn-1nn-1),
其中n1,n2,…,nn-1线性无关,就是说n0,n1,n2,…,nn-1线性相关,且它们的秩等于n-1,于是由代数学知识,由n0,n1,n2,…,nn-1构成的n×n矩阵的行列式

从而,u=f(x1,x2,…,xn)在φi(x1,x2,…,xn),i=1,2,…,n-1以点P0为极值点的必要条件就简化为在该点处满足
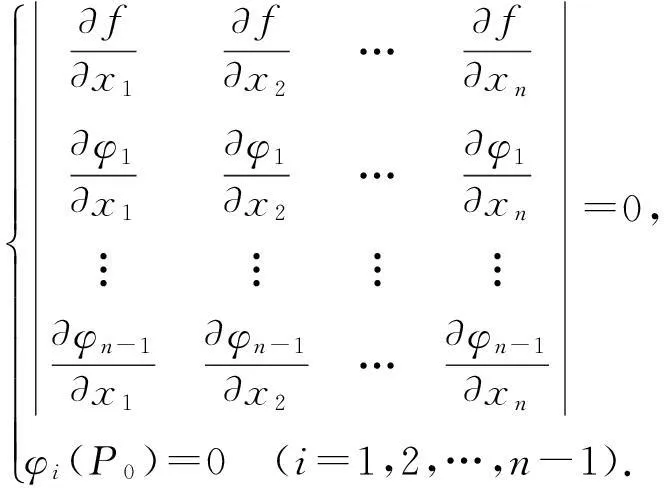
推论1.2设f(x,y),φ(x,y)具有一阶连续偏导数,且φy(x,y)≠0(或φx(x,y)≠0),则函数z=f(x,y)在条件φ(x,y)=0下以点P0(x0,y0)为极值点的必要条件是在该点满足等式

推论1.3设f(x,y,z),φ(x,y,z),ψ(x,y,z)具有一阶连续偏导数,且
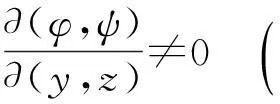
则u=f(x,y,z)在条件
φ(x,y,z)=0,ψ(x,y,z)=0
下以点P0(x0,y0,z0)为极值点的必要条件是在该点满足
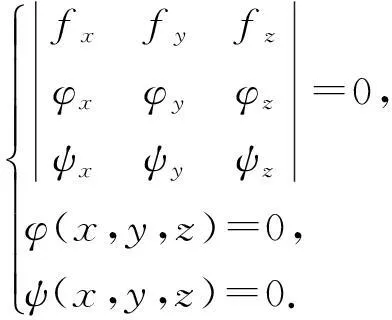
注函数的极值点是特性非常鲜明的几何点,也可以利用多元函数条件极值点的几何性质对这两个推论予以直观的解释.
(i)z=f(x,y)在条件φ(x,y)=0下以点P0(x0,y0)为条件极值点的必要条件是
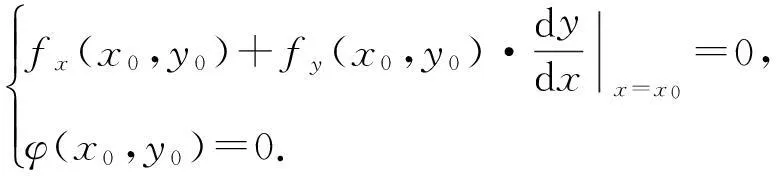


用行列式表示即为所证结论.
(ii)u=f(x,y,z)在φ(x,y,z)=0,ψ(x,y,z)=0下以点P0(x0,y0,z0)为极值点的必要条件是
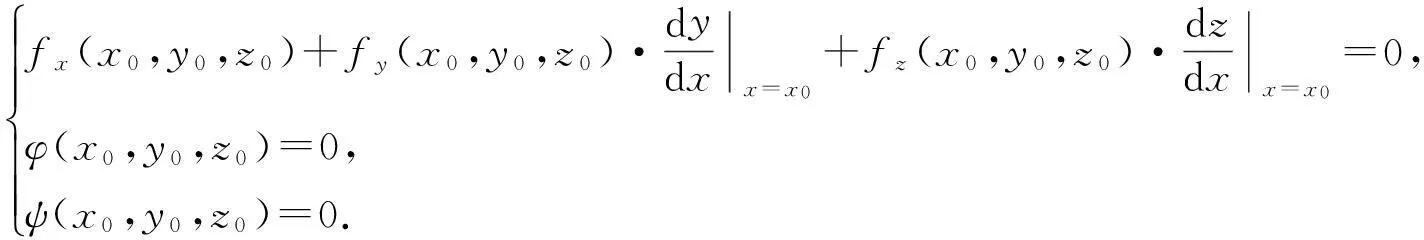
(6)
由φ(x,y,z)=0,ψ(x,y,z)=0知,

(7)
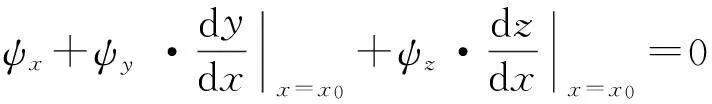
(8)

在极值点P0处的切向量,向量
n=(fx(x0,y0,z0),fy(x0,y0,z0),fz(x0,y0,z0)),n1=(φx,φy,φz),n2=(ψx,ψy,ψz)
分别是曲面
f(x,y,z)=c,φ(x,y,z)=0,ψ(x,y,z)=0
在点P0(x0,y0,z0)处的法向量,由上述(6),(7),(8)式知n⊥T,n1⊥T,n2⊥T,可见n,n1,n2同位于曲线Γ在极值点P0处的法平面上,即n,n1,n2共面,从而有
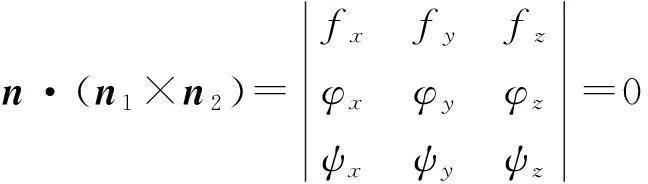
到此,得到了二元、三元及一般n元函数在等式约束条件下取得极值的必要条件,相比Lagrange乘数法,这些用行列式表示的条件没有Lagrange乘子的干扰,简化了方程组的求解,降低了极值点的寻找难度.
[参考文献]
[1]齐德鹏.一个求解条件极值问题的极值点的新方法[J].大学数学,2013,29(4):107-112.
[2]朱玉清,于育民. 多元函数条件极值的解法研讨[J].河南教育学院学报:自然科学版,2008,17(3):28-29.
[3]吴赣昌.高等数学(下册)[M].北京:中国人民大学出版社,2009:100-101.
[4]北京大学数学系几何与代数教研室前代数小组.高等代数[M].北京:高等教育出版社,2003:131-134.
[5]同济大学数学系.高等数学(下册)[M].北京:高等教育出版社,2007:114-115.
[6]乔建斌,魏巍.一种Lagrange乘数法及其推广的新证明[J].青岛科技大学学报:自然科学版,2013,34(3):318-321.
[7]张秀梅.三元函数双条件极值的一个必要条件[J].辽宁工业大学学报:自然科学版,2012,32(2):138-140.
Necessary Conditions for Constrained Extreme Value of Tri-Function
ZHANGDong-yan,WANGYao-ge,ZHANGWu-jun
(Science Institute Information Engineering University,Zhengzhou 450000, China)
Abstract:The paper provides an entire derivation of necessary conditions represented by determinant for conditional extreme value of multivariate function, binary function and ternary function under the equality constraints. And geometrical interpretations are presented to explain the necessary conditions for conditional extreme value of binary, ternary function. These necessary conditions simplify the solution of the constrained extreme value problem as they avoid the interference of Lagrange multiplicator in solving the final equation.
Key words:multivariate function; constrained extreme value; necessary conditions
[中图分类号]O172
[文献标识码]C
[文章编号]1672-1454(2015)05-0098-06
[收稿日期]2014-11-13;[修改日期]2015-07-12
定理1.1设
f(x1,x2,…,xn),φi(x1,x2,…,xn),i=1,2,…,k
均具有一阶连续偏导数,φi(x1,x2,…,xn), i=1,2,…,k对各个变量的偏导数不全为零,且

线性无关,则u=f(x1,x2,…,xn)在条件
φi(x1,x2,…,xn)=0,i=1,2,…,k
下以点P0为极值点的必要条件是
φi(P0)=0,i=1,2,…,k
且在该点处矩阵

的任意n-k个k+1级子式等于零.
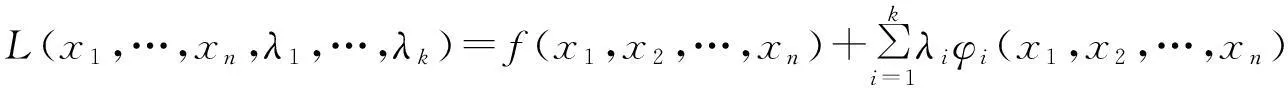
由文[3]知,在定理条件下u=f(x1,x2,…,xn)在P0处取极值的必要条件是在该点处满足

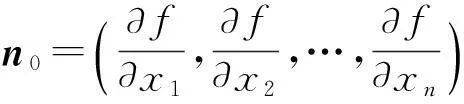
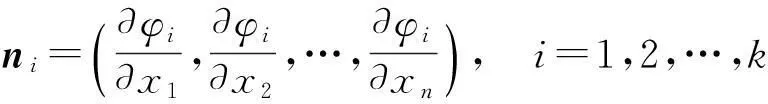
分别是f(x1,x2,…,xn)=c和φi(x1,x2,…,xn)=0的法向量.下面依然寻找可简化方程组(1)的行列式.注意到方程组(1)用向量ni,i=0,1,2,…,k可表示为
n0=-(λ1n1+λ2n2+…λknk),
其中n1,n2,…,nk线性无关,也就是说n0,n1,n2,…,nk线性相关,且它们的秩等于k,于是以n0,n1,n2,…,nk为行向量的矩阵

的秩为k.而由代数学知识,矩阵秩为k的充要条件是矩阵所有k+1级子式等于零[4].这里我们要找的是方程组(1)中变量x1,x2,…,xn需满足的等式,因此只需任取其中n-k个k+1级子式,即和方程组(2)共同构成了极值点P0的坐标需满足的等式.
显然,若定理中n=3,三元函数u=f(x,y,z)在条件φ(x,y,z)=0下取得极值的必要条件就是:
推论1.1设f(x,y,z),φ(x,y,z)具有一阶连续偏导数,且φz(x,y,z)≠0(或φx,φy不全为零),则u=f(x,y,z)在条件φ(x,y,z)=0下以点P0(x0,y0,z0)为极值点的必要条件是在该点满足

证u=f(x,y,z)在约束条件下以点P0(x0,y0,z0)为条件极值点的必要条件是在该点满足
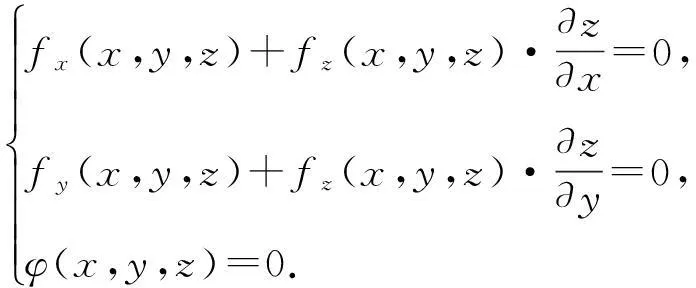
(3)
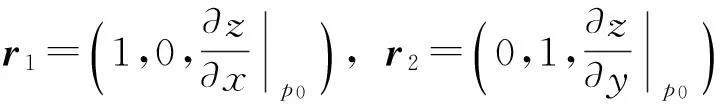
n=(fx(x0,y0,z0),fy(x0,y0,z0),fz(x0,y0,z0)),
则方程组(3)的前两个条件表明n⊥r1,n⊥r2,也就是说在极值点P0(x0,y0,z0)处目标函数的等值曲面f(x,y,z)=c与曲面Σ:φ(x,y,z)=0有公共切平面,等值曲面与曲面Σ在P0(x0,y0,z0)处的法向量共线,即在极值点处必有n∥r1×r2,又
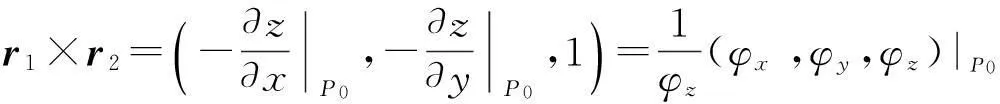
从而在P0(x0,y0,z0)处有
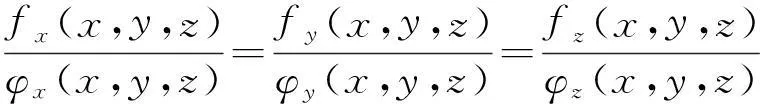
用行列式表示即得所证结论.
1.2 函数u=f(x1,x2,…,xn)在n-1个条件φi(x1,x2,…,xn)=0,i=1,2,…,n-1下的极值
定理1.2设
f(x1,x2,…,xn),φi(x1,x2,…,xn),i=1,2,…,n-1
均具有一阶连续偏导数,φi(x1,x2,…,xn),i=1,2,…,n-1对各个变量的偏导数不全为零,且
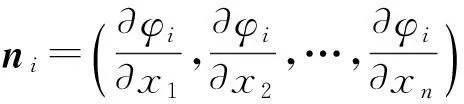
线性无关,则u=f(x1,x2,…,xn)在φi(x1,x2,…,xn),i=1,2,…,n-1以点P0为极值点的必要条件是在该点处满足
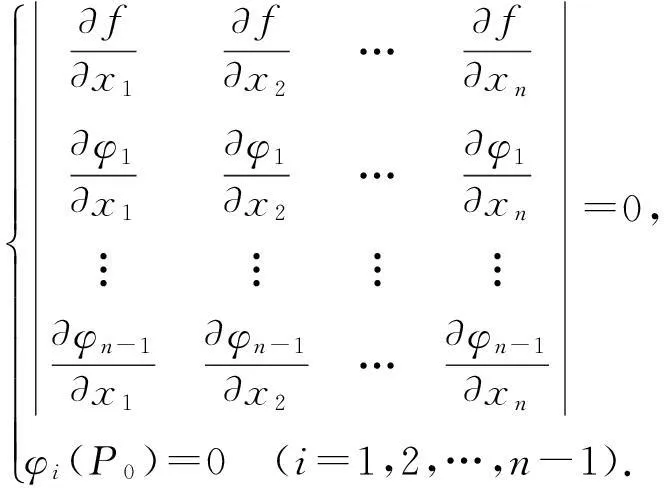
证令

由文[5],已知条件下u=f(x1,x2,…,xn)在φi(x1,x2,…,xn),i=1,2,…,n-1下在点P0处取得极值的必要条件是在该点满足

记f(x1,x2,…,xn)=c的法向量

则方程组(4)可表示为
n0=-(λ1n1+λ2n2+…λn-1nn-1),
其中n1,n2,…,nn-1线性无关,就是说n0,n1,n2,…,nn-1线性相关,且它们的秩等于n-1,于是由代数学知识,由n0,n1,n2,…,nn-1构成的n×n矩阵的行列式

从而,u=f(x1,x2,…,xn)在φi(x1,x2,…,xn),i=1,2,…,n-1以点P0为极值点的必要条件就简化为在该点处满足
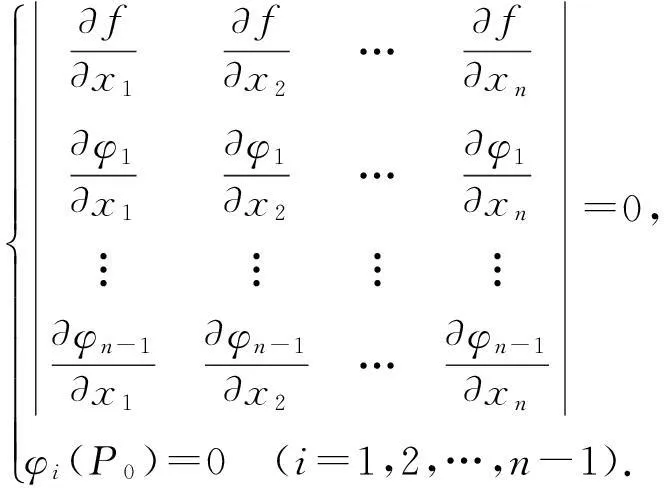
推论1.2设f(x,y),φ(x,y)具有一阶连续偏导数,且φy(x,y)≠0(或φx(x,y)≠0),则函数z=f(x,y)在条件φ(x,y)=0下以点P0(x0,y0)为极值点的必要条件是在该点满足等式

推论1.3设f(x,y,z),φ(x,y,z),ψ(x,y,z)具有一阶连续偏导数,且
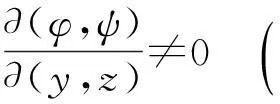
则u=f(x,y,z)在条件
φ(x,y,z)=0,ψ(x,y,z)=0
下以点P0(x0,y0,z0)为极值点的必要条件是在该点满足
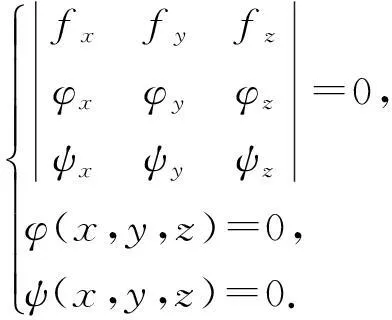
注函数的极值点是特性非常鲜明的几何点,也可以利用多元函数条件极值点的几何性质对这两个推论予以直观的解释.
(i)z=f(x,y)在条件φ(x,y)=0下以点P0(x0,y0)为条件极值点的必要条件是
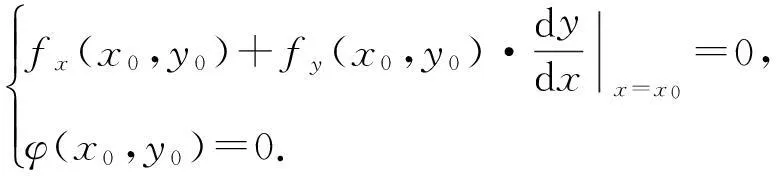


用行列式表示即为所证结论.
(ii)u=f(x,y,z)在φ(x,y,z)=0,ψ(x,y,z)=0下以点P0(x0,y0,z0)为极值点的必要条件是
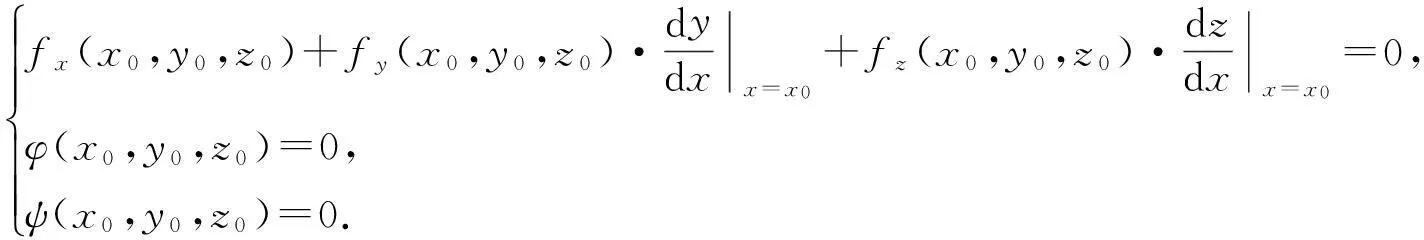
(6)
由φ(x,y,z)=0,ψ(x,y,z)=0知,

(7)
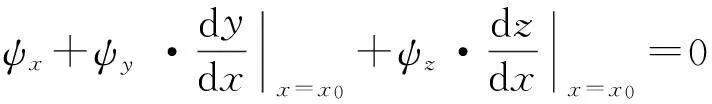
(8)

在极值点P0处的切向量,向量
n=(fx(x0,y0,z0),fy(x0,y0,z0),fz(x0,y0,z0)),n1=(φx,φy,φz),n2=(ψx,ψy,ψz)
分别是曲面
f(x,y,z)=c,φ(x,y,z)=0,ψ(x,y,z)=0
在点P0(x0,y0,z0)处的法向量,由上述(6),(7),(8)式知n⊥T,n1⊥T,n2⊥T,可见n,n1,n2同位于曲线Γ在极值点P0处的法平面上,即n,n1,n2共面,从而有
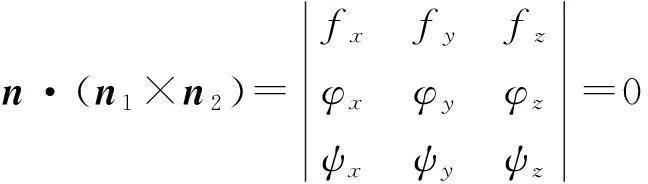
到此,得到了二元、三元及一般n元函数在等式约束条件下取得极值的必要条件,相比Lagrange乘数法,这些用行列式表示的条件没有Lagrange乘子的干扰,简化了方程组的求解,降低了极值点的寻找难度.
[参考文献]
[1]齐德鹏.一个求解条件极值问题的极值点的新方法[J].大学数学,2013,29(4):107-112.
[2]朱玉清,于育民. 多元函数条件极值的解法研讨[J].河南教育学院学报:自然科学版,2008,17(3):28-29.
[3]吴赣昌.高等数学(下册)[M].北京:中国人民大学出版社,2009:100-101.
[4]北京大学数学系几何与代数教研室前代数小组.高等代数[M].北京:高等教育出版社,2003:131-134.
[5]同济大学数学系.高等数学(下册)[M].北京:高等教育出版社,2007:114-115.
[6]乔建斌,魏巍.一种Lagrange乘数法及其推广的新证明[J].青岛科技大学学报:自然科学版,2013,34(3):318-321.
[7]张秀梅.三元函数双条件极值的一个必要条件[J].辽宁工业大学学报:自然科学版,2012,32(2):138-140.
Necessary Conditions for Constrained Extreme Value of Tri-Function
ZHANGDong-yan,WANGYao-ge,ZHANGWu-jun
(Science Institute Information Engineering University,Zhengzhou 450000, China)
Abstract:The paper provides an entire derivation of necessary conditions represented by determinant for conditional extreme value of multivariate function, binary function and ternary function under the equality constraints. And geometrical interpretations are presented to explain the necessary conditions for conditional extreme value of binary, ternary function. These necessary conditions simplify the solution of the constrained extreme value problem as they avoid the interference of Lagrange multiplicator in solving the final equation.
Key words:multivariate function; constrained extreme value; necessary conditions
[中图分类号]O172
[文献标识码]C
[文章编号]1672-1454(2015)05-0098-06
[收稿日期]2014-11-13;[修改日期]2015-07-12

