二次曲线的对称性及曲率

郭芳承，王艳琰

(陇东学院 数学与统计学院, 甘肃 庆阳 745000)

对特定几何对象进行分类是几何学研究的重要问题之一[1-4]，二次曲线是初等几何和高等几何的重要研究对象，二次曲线一般理论的一个重要方面是对其进行分类[5-7]。然而，分类的一个关键步骤是对其进行化简，找到各类二次曲线的标准形式[8-11]。采用代数学的技巧，用不变量对二次曲线进行化简是所有化简方法中最简洁的一种，但严重缺乏几何直观。

容易发现，二次曲线的图形都具有高度的对称性，从几何上看，以对称轴为坐标轴时，二次曲线的表达式最为简单，为二次曲线的标准形式。因此，讨论二次曲线的对称中心和对称轴对化简二次曲线具有重要作用。

平面上，二元二次方程

F(x，y)=a11x2+2a12xy+a22y2+2a13x+2a23y+a33=0

(1)

表示的曲线称为二次曲线。定义三阶对称矩阵

二次曲线(1)又可表达为

1 二次曲线的对称中心

定义1 对于一条二次曲线，若平面上有一固定点，它是该二次曲线的所有经过它的弦的中点，则该点是二次曲线的一个对称中心，简称二次曲线的中心。

若二次曲线的中心存在，它既可能在二次曲线上，如两条相交直线的情形；也可能在二次曲线之外，如椭圆和双曲线等，存在中心的二次曲线的图像具有高度的对称性。下面讨论二次曲线中心存在的条件，二次曲线中心的个数，以及中心的坐标等。

设点C(x0，y0)是二次曲线(1)的中心，过点C且以(X:Y)为方向的直线为

(2)

或

(3)

将(2)或(3)代入(1)得

Φ(X，Y)t2+2[F1(x0，y0)X+

F2(x0，y0)Y]t+F(x0，y0)=0

(4)

其中Φ(X，Y)=a11X2+2a12XY+a22Y2，且

方程(4)是参数t的一元二次方程，其两根t1与t2分别对应于直线l0与二次曲线的两个交点，而点C为两个交点的中点，故t1+t2=0，进而有

F1(x0，y0)X+F2(x0，y0)Y=0

由直线l0的方向的任意性知道，中心C(x0，y0)满足方程组

记

由线性代数理论，易知有如下结论。

定理1 对于二次曲线(1)，(I)当I2≠0时，二次曲线有唯一中心，其坐标为

2 二次曲线的对称轴

定义2 在平面上，若存在一条直线，与之垂直的二次曲线的弦的中点都在该直线上，称该直线为二次曲线的一条对称轴。

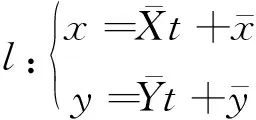
同时，设直线

将直线l′的方程带入二次曲线的方程(1)，有

(5)

(6)

根据对称轴的定义，有

(7)

即

(8)

整理得

(9)

下面的结论给出了中心二次曲线的对称轴的存在性。

证明 对于中心二次曲线，由(8)知，二次曲线的中心必在所有的对称轴上，而中心二次曲线有唯一中心，故对称轴的个数等价于对称轴方向的个数。

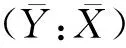
Δ=(a11-a22)2+4a12>0

从而，二次曲线有两个对称轴方向

易见这两个方向相互正交。

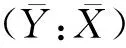
这时，二次曲线或为圆，或为虚圆，或为圆点。

对于非中心二次曲线，有如下结论。

定理3 对于非中心二次曲线(1)(I2=0)，(I)若a12≠0，则二次曲线有唯一一条对称轴

(a11a13+a12a23)=0

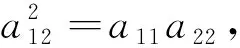
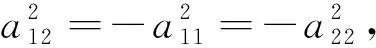
3 利用对称性化简二次曲线

若二次曲线(1)为中心二次曲线，由方程(9)得两条对称轴的方向

进而由方程(8)得到两条对称轴的方程为

显见这两条直线相互正交，交点为二次曲线的中心。以这两条对称轴作为新的坐标轴，建立坐标变换，代入原二次曲线的方程(1)即可化简该二次曲线。

例1 化简二次曲线8x2+4xy+5y2+8x-16y-16=0。

解a11=8，a12=2，a13=4

a12=2，a22=5，a23=-8

易见，该二次曲线为中心二次曲线，对称轴方向

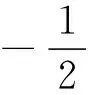
进而两条对称轴为

l1:x-2y+5=0

l2:2x+y=0

以l1做新坐标系的y′-轴，l2做新坐标系的x′-轴，得到坐标变换公式

(10)

进而

将其代入二次曲线的方程，整理得

图1 注：1.在选择新的坐标轴的时候，为确保定向不变，要求(10)中 等号右侧的系数行列式的值大于零；2.要根据直线与原坐标轴 的交点坐标判断坐标轴的正向；3.为保证新坐标轴与原坐标轴 长度单位不变，须在变换公式(10)左边乘以方向向量的模长.

若二次曲线(1)为无心二次曲线，即满足

将以上对称轴方程的参数方程代入二次曲线的方程(1)，容易发现二次曲线与该对称轴只有一个交点，称为二次曲线的顶点，其坐标为

(x0，y0)=

(11)

其中

(12)

对于无心二次曲线，以对称轴(11)和直线(12)为坐标轴建立新坐标系，可以对二次曲线进行有效化简。

例2 化简二次曲线x2+2xy+y2+2x+y=0。

易见该二次曲线为无心二次曲线，直接计算得到对称轴的方程为

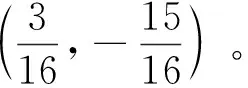
以l1为x′-轴，l2为y′-轴，得到坐标变换公式

解出x与y得

将其代入二次曲线方程整理得到

图2

若二次曲线(1)为线心二次曲线，即满足

由定理3，线心二次曲线有唯一一条对称轴

a12x+a22y+a23=0

即中心直线。

在中心直线上任取一点作为新的坐标原点，以过该点与中心直线垂直的直线和中心直线为新的坐标轴，建立坐标变换，可以快速化简二次曲线。

例3 化简二次曲线x2-2xy+y2+2x-2y-3=0。

易见，该二次曲线是线心二次曲线，其唯一的对称轴

l1:x-y+1=0

为建立新坐标轴，再另外任取一条与l1垂直的直线

l2:x+y=0

以l1为y′-轴，l2为x′-轴，得到坐标变换公式

解出x与y得

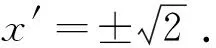
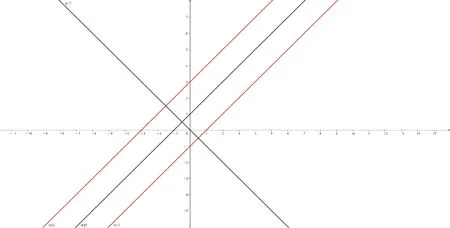
图3

4 二次曲线的曲率

对二次曲线(1)，记

Fx(x，y)=2(a11x+a12y+a13)

Fy(x，y)=2(a12x+a22y+a23)

并记矩阵A的行列式为I。化简后的二次曲线方程表达式为

F(x，y)=a11x2+a22y2+a33=0

(13)

定理4 二次曲线(1)上正则点P(x，y)处曲率

对化简后的二次曲线方程(13)，曲率

其中，F(x，y)=0.

证明 设F(x，y)=0在正则点P(x，y)处有显式表达y=f(x)，求导得

设曲线在点P(x，y)处有向量式参数方程

则曲线的曲率可以表达为

直接计算得

从而

直接计算得

进而

对于线心二次曲线，行列式I=0，从而有如下结论。

推论1 线心二次曲线的曲率为零，即线心二次曲线只能由直线构成。