频率编码和调制原理在Hodgkin-Huxley系统上的应用

唐伟伟，　檀结庆，　唐元华

(1. 合肥工业大学数学学院，合肥230009；

2.ResearchBioinformatics，CompleteGenomics，Inc.，MountainView，California，USA.)



频率编码和调制原理在Hodgkin-Huxley系统上的应用

唐伟伟1，檀结庆1，唐元华2

(1. 合肥工业大学数学学院，合肥230009；

2.ResearchBioinformatics，CompleteGenomics，Inc.，MountainView，California，USA.)

[摘要]频率编码指感觉神经元在受到刺激后产生膜电位的周期变化，变化的频率往往与刺激的强度成正比.本文在Hodgkin-Huxley系统的基础上，对其微分方程进行简化；对于频率编码，给出去耦时间尺度上的微分方程系统；研究在单一参数系统下，频率编码行为的变化规律.

[关键词]神经刺激； 频率编码；Hodgkin-Huxley系统； 奇异摄动系统； 调频机制

1引言

感觉神经元可根据刺激强度的变化作出相应的频率调制.振荡频率通常是正比于刺激的强度，理解为输入的模拟信号被频率编码.当刺激强度越大，神经元被激发的速率会越快；当刺激强度越小，神经元被激发的速率会越慢.当然，这个调频机制具有一定的线性范围.如果一个信号太弱，可能无法侦测到它；反之，如果信号过于强大，神经系统不堪重负，甚至可能会彻底关闭对刺激的响应.

自从首次刊登Hodgkin-Huxley具有里程碑意义的成果后[1]，可以用微分方程系统来呈现一个神经元的调频机制，这个方程系统同样具有频率编码的能力.

假设对一个可兴奋系统输入一个模拟信号S(t)，那么输出信号F(t)就是一个频率编码.随着模拟信号的强度变化，输出频率也作出相应的变化.因此，通过观察输出的频率，我们可以猜测模拟输入的量.模拟信号以某种方式被转化为具有周期的频率信号.

一个神经元系统可以通过一组微分方程来近似模拟，这组微分方程用来呈现由细胞膜表面离子通道活动而引起的膜电位的变化[2].从数学角度，先介绍一种最简单的系统，它用来描述可激发介质中的行为，这个系统由两个微分方程组成[3]：

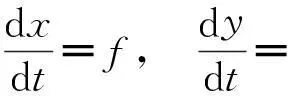
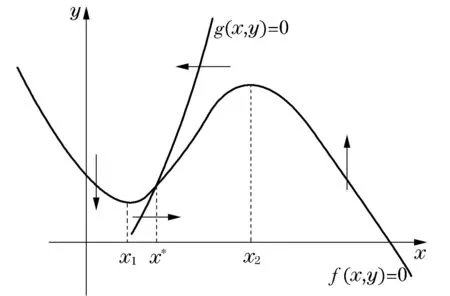
图1　典型的可激发系统

当交点x*在x1和x2之间时，系统不稳定，并且是振荡的；当交点x*在x1左边时，系统是稳定的，并且是可激发的；当交点x*在x2右边时，系统是稳定的，并且不可激发.

2简化Hodgkin-Huxley微分方程系统

2.1　Hodgkin-Huxley方程

Hodgkin-Huxley系统将乌贼轴突神经元行为赋予了数学形式.以下是Hodgkin-Huxley微分方程组系统的原始形式[1]：

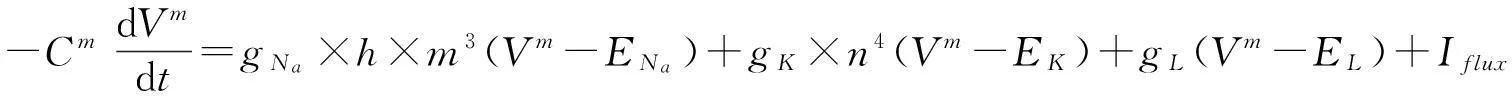
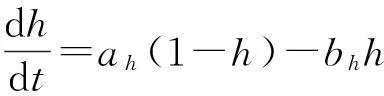
(1)

Hodgkin-Huxley系统是由一个表示膜电位的方程及附加的三个表示通道门控的方程组成的.Na+离子通道是由两个门控变量m和h来支配的，m表示激活状态门控系数，h表示失活状态门控系数.K+离子通道仅由一个门控变量n来支配，表示激活状态门控系数.方程中没有给出K+离子通道的失活状态门控系数.尽管如此，K+离子通道，作为一个延迟外流控制器，当到达一定程度时也会有失活状态.但是，在正常情况下，它对于神经元行为来说是多余的.

2.2　简化Hodgkin-Huxley方程

下面介绍如何将Hodgkin-Huxley系统简化到只含两个微分方程的系统.首先，Na+离子的激活过程非常迅速，通常在1ms内完成.假设通道的激活状态总是在预定的时间尺度上完成.可以将原系统的快动作微分方程改为代数方程，即

0=am(1-m)-bmm.

其次，Na+离子失活过程和K+激活过程几乎是在同一时间尺度上进行的.它们的变化速率几乎是相同的，因此用同一个门控变量来表示就足够了.在这里，用0.5-n4来代替h，替换后，可以保证h>0，并且h总是与n步调相反.

于是得到两个方程的Hodgkin-Huxley系统:

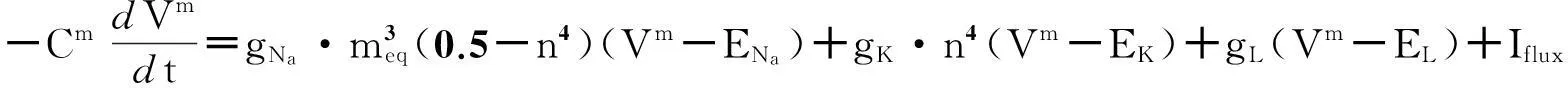
(2)

方程(2)相对于原始方程(1)来说，使Hodgkin-Huxley系统变得简单明了，因此更容易被理解和分析.它可以更有效的帮助我们理解神经元细胞的复杂生理行为.

这并不是大家第一次简化Hodgkin-Huxley系统.在这之前，Fitzhuh-Nagoma方程[4]将原始系统简化成两个微分方程系统，即是FitzHugh-Nagumo模型[5]：

图2展示了简化Hodgkin-Huxley系统后所得方程(方程2)的nullclines.令dV/dt=0，得到一条N形曲线(图2中的黑线)；令dn/dt=0，得到一条单调递增曲线(图2中的红线).N形曲线(dV/dt=0)有一个局部极大值点和一个局部极小值点.从图2中两条曲线的交点可以得出，系统是振荡的.与原始Hodgkin-Huxley系统相比，简化后的方程显示相同的性质.

图2　简化后Hodgkin-Huxley系统(方程2)的Null clines

3频率编码理论

3.1　奇异摄动系统

在本节中，我们研究微分方程组系统的频率编码，并给出一些初步研究结果.着重点是，解出下面这个微分方程组系统(方程3)的周期解[6].

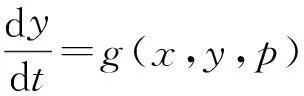
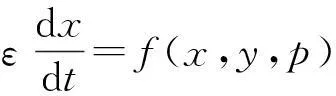
(3)

其中x∈m，y∈n.p∈k是一个参变量，ε是一正数，并且足够小.f和g是定义在n+m上的函数.

在方程(3)中，如果f(x，y，p)是一阶无穷小o(1)，相对于变量y，变量x随时间t变化的速度更快.这表示变量x相对于变量y是快变量.总的来说，方程组(3)中，快动作系统是由第二个微分方程决定的；慢动作系统是由第一个微分方程决定的.

在物理学和生物学当中，有许多振荡系统或可兴奋系统都可以写成方程(3)这样的形式.例如，Van der Pol’s 方程[7].

方程(3)中，令ε=0，得到其所对应的退化系统，即方程(4)

f(x，y，p)=0，

(4)

其中x和y是标量变量，参数p固定不变.(3)中第二个方程定义了相平面2上一曲线Γ.假设在曲线Γ上，

(fx(x，y，p))2+(fy(x，y，p))2>0，

曲线Γ上，使fx(x，y，p)=0的点为奇异点，否则为非奇异点.假设Γ上奇异点是孤立的，并且fxx(x，y，p)≠0.

根据Implicit Function Theorem[8]，在非奇异点上，可用y=F(x，p)来表示曲线Γ.满足fx(x，y，p)<0点的集合为曲线Γ的稳定部分(stable)；满足fx(x，y，p)>0点的集合为曲线Γ的不稳定部分(unstable)；这两部分被奇异点fx(x，y，p)=0隔开.以下给出方程(3)的不连续解.此方程的解由有限次慢动作与快动作交替组成.

慢动作代表曲线Γ上的稳定部分；快动作代表曲线Γ上的不稳定部分，它几乎是瞬间完成的.在节点fx(x，y，p)=0处，慢动作向快动作转化. 若在(x，y)平面上，不连续解是一极限环Z0，我们称Z0是方程(4)的不连续周期解.不连续解的周期为

(5)

在方程(4)中，T0仅由慢动作部分所用时间组成.快动作部分所用时间为零.

定理1假如方程(4)有一极限环Γ0，并且满足上述条件，那么对于一足够小ε，其非退化系统，即方程(3)有唯一且稳定极限环Zε，当ε→0时，Zε一致收敛于Z0.另外，Zε的周期为

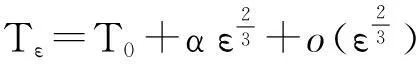
(6)

其中，α为一常量，o(ε)是ε的高阶无穷小，当ε→0.

参考文献[8]中给出定理1的证明过程.关于Γ0周期解的实值近似，慢动作部分是ε的无穷小，快动作部分是εa的无穷小，其中a≥2/3.在节点附近，近似值为εa的无穷小，其中a≥0.然而，在节点附近没有给出a的下界.这种近似方法我们称之为零级近似[6].

定理2令εM=max(ε1，ε2)，ε1和ε2足够小.若退化系统，即方程(4)有极限环Γ0，并且满足定理1的条件，那么有

(i) 对εi，方程(3)有周期解φ(t，εi)，i=1，2；

(iii) Tε1-Tε2=o((εM)2/3).

定理1可以被扩展到x和y都是矢量变量的情形，并且结论非常相似.但是在扩展的过程中，要引入一些附加的条件.

3.2　单一缩放系数的慢动作系统

假设m=n=1，即x∈，y∈，进一步假设能够从g(x，y，p)中将h提取出来，并作为一缩放系数放在前面，即g(x，y，p)).其他参数不变，并且h不出现在f(x，y，p)中.基于以上假设，可将方程(3)写成下面这种形式：

(7)

这里x和y是标量变量，h 是参变量，并且h>0，ε1是一很小的参数.

令h=h0，有

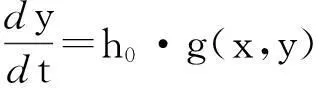
(8)

方程(8)对应的退化系统为

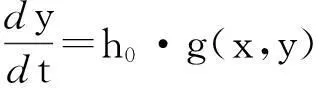
f(x，y)=0.

(9)

假设，方程(9)有一周期解φ(t，h0，0)，根据上一节定义，其周期为T(h0，0).由定理2，知道对于一很小的值ε1，方程(8)也有一周期解φ(t，h0，ε1).此外，方程(7)的周期解φ(t，h，ε1)在轨迹和周期上非常接近方程(9)的周期解φ(t，h0，0).

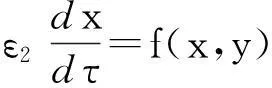
(10)

定理3假设方程(9)满足定理1 的条件，并且，r=h/h0不是太大.那么有以下结论：

(i) 对应方程(9)的周期解φ(t，h0，0)，方程(7)有周期解φ(t，h)；

(ii) 方程(7)解φ(t，h)的周期，即T(h)与方程(8)解φ(t，h0)的周期，即T(h0)满足

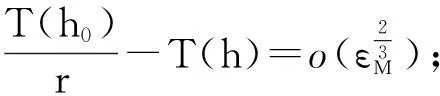
(iii)方程(7)周期解φ(t，h)与方程(8)周期解φ(t，h0)满足

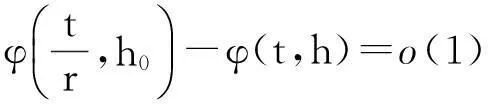
定理3说明，随着h的变化，方程(3.6)依然可以频率编码.例如，若h=2h0，有r=2.根据定理3，当h=2h0时，解的周期为

图3说明在不同h值下，膜电位振荡模式.当h加倍，振荡频率加倍.

(a) h=1　　　　　　　(b)h=0.5图3　膜电位振荡模式

3.3　不同缩放系数的慢动作系统

假如f(x，y)=0有一局部极小值x1和一局部极大值x2，并且退化系统周期解由四个部分组成.考虑

(11)

定理4假设方程(11)满足正则性条件.令εM=max(εS1，εS2，εS0).对于足够小的εM，εM>0有

(i) 系统(11)有解φ(t，S1，S2，ε)，周期为T(S1，S2，ε)，相对于方程(11)的周期解φ(t，S0，S0，ε)，周期为T(S0，S0，ε).另外，

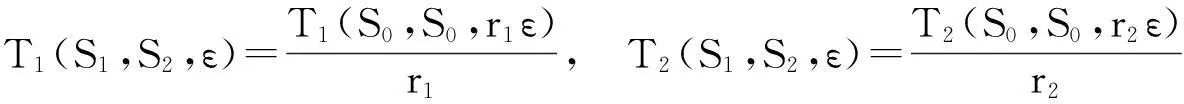
(ii)

及

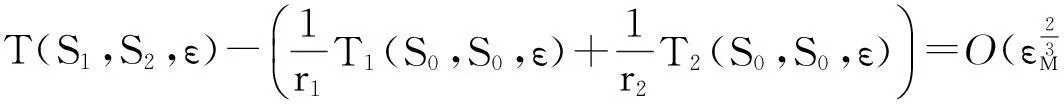
(12)

(iii)

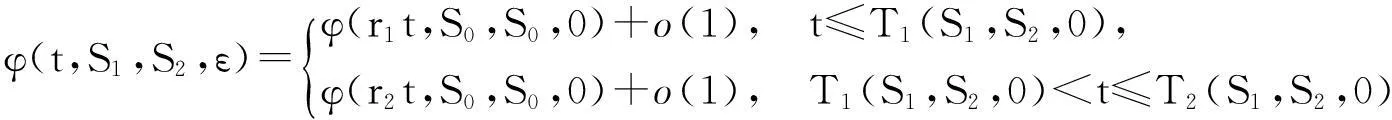
及

(13)

定理3与定理4 的不同之处是，定理4 将慢动作部分分为两个部分.令S2=S0，通过改变S1，S1>1，可以在不改变波峰宽度的情况下，改变恢复时间，从而达到改变振荡频率的目的；或者令S1=S0，通过改变S2，S2>1，在不改变恢复时间的情况下，改变波峰宽度，同样达到改变振荡频率的效果.如果令S1=S2改变缩放系数r.波峰宽度及恢复时间同时改变.

图4说明在不同S1，S2值下，膜电位的振荡模式.

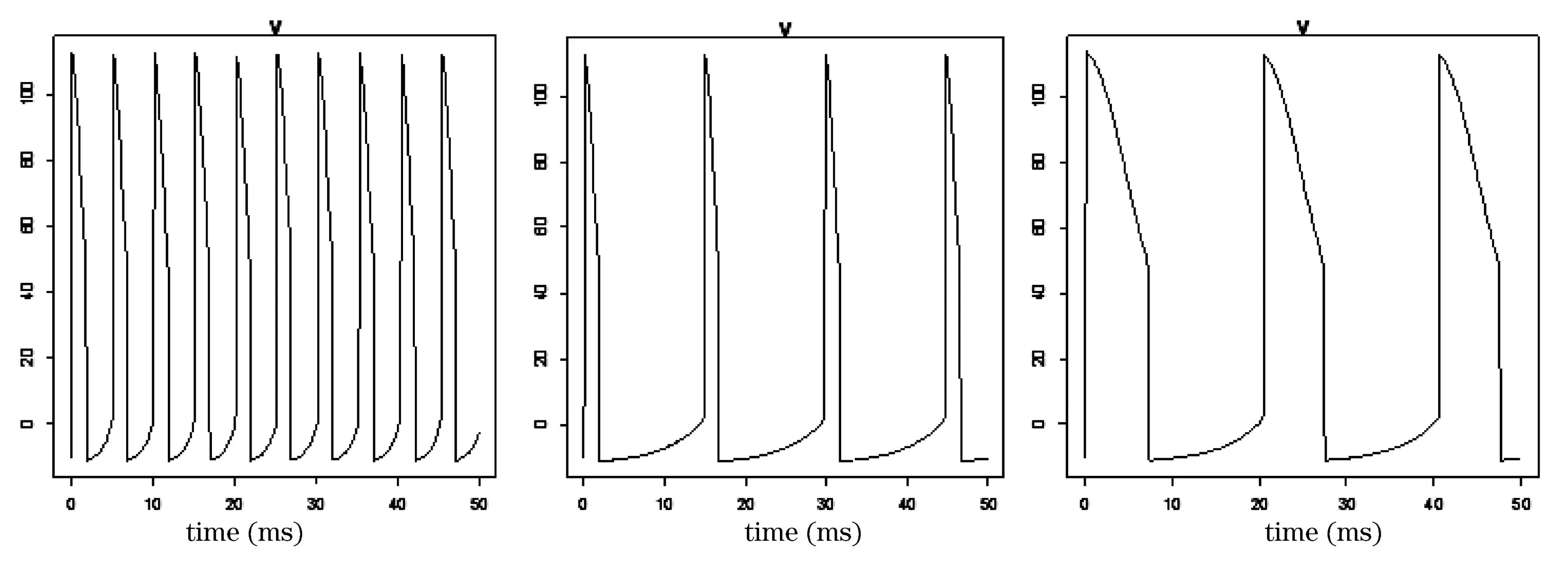
(a) S1=S2=1　　　(b) S1=0.25, S2=1　　　(c) S=1, S2=0.25图4　膜电位振荡模式

最后，解决调频机制的问题.如果有一随时间变化的信号，将此信号引入系统，那么系统的频率是如何变化的，如图5所示.反之，如果观察到系统中频率发生改变，能推导相对应输入的模拟信号吗？ 这个问题非常复杂，并牵扯到多时间尺度.这里给出一个最简单结论.假设输入的模拟信号是分段函数，在这一假设条件下，可衍生出一公式，这个公式反应输入信号与输出频率的关系.

图5　膜电位振荡模式S1(t)=1+sin(2π(t/1000)-π/2)

4结论与认识

将系统从二维平面推广到更高维空间.

(14)

Hodgkin-Huxley系统就是一个案例.在HH系统中，改变某个离子通道的状态只能一次调整系统振荡频率.目前能够诠释这种系统的最佳方法是仿真模拟.关于研究心脏窦房结(SA节点)机制，我们已经找到一个非常好的模型[9]，这个模型反应电信号及振荡行为.但是， 神经递质是如何影响心率调节的呢？我们知道在恢复阶段，有多重电流被激活，例如A-current[10].但是在细胞中， A-current 是如何调整频率编码的[11].这些问题有待于研究.

[1]HodgkinAL，HuxleyAF.Aquantitativedescriptionofmembranecurrentanditsapplicationtoconductionandexcitationinnerve[J].TheJournalofphysiology， 1952， 117(4): 500-544.

[2]HodgkinAL，HuxleyAF.CurrentscarriedbysodiumandpotassiumionsthroughthemembraneofthegiantaxonofLoligo[J].TheJournalofphysiology, 1952， 116(4): 449-472.

[3]TangY，OthmerHG.Frequencyencodinginexcitablesystemswithapplicationstocalciumoscillations[J].Proc.NationalAcademySciences, 1995， 92(17): 7869-7873.

[4]FitzHughR.Impulsesandphysiologicalstatesintheoreticalmodelsofnervemembrane[J].BiophysicalJournal, 1961， 1(6): 445-466.

[5]NagumoJ，ArimotoS，YoshizawaS.Anactivepulsetransmissionlinesimulatingnerveaxon[J].ProcIRE, 1962， 50(10):2061-2070.

[6]TangY.TheoreticalStudiesonSecondMessengerDynamics[M].AnnArboor,Michigan:UniversityMicrofilms,ProQuestLIC., 1993.

[7]VanderPolB.Onrelaxation-oscillations[J].TheLondon，EdinburghandDublinPhil.Science1927， 2(7): 978-992.

[8]MishchenkoEF，RosovNK.DifferentialEquationswithSmallParametersandRelaxationOscillations[M].NewYork:PlenumPress, 1980.

[9]NobleD.Modellingtheheartfromgenestocellstothewholeorgan[J].Science, 2002， 295(5560): 1678-1682.

[10]RushME，RinzelJ.ThepotassiumA-current，lowfiringratesandreboundexcitationinHodgkin-Huxleymodels[J].BulletinofMathematicalBiology, 1995， 57(6): 899-929.

[11]ConnerJA，StevensCF.Predictionofrepetitivefiringbehaviourfromvoltageclampdataonanisolatedneuronesoma[J].TheJournalofPhysiology, 1971， 213(1): 31-53.

TheoryofFrequencyEncodingandModulationwith

ApplicationtotheHodgkin-HuxleySystem

TANG Wei-wei1，TAN Jie-qing1，TANGY.Tom2

(1.DepartmentofMathematics，HefeiUniversityofTechnology，Hefei230009，China;

2.ResearchBioinformatics，CompleteGenomics，Inc.，MountainView，California，USA.)

Abstract:Sensoryneuronsrespondtostimulatorysignalswithperiodicfiringsofthemembranepotential.Thefrequencyoffiringisoftenproportionaltotheintensityofstimulus，andonesaysthatthestimulusisfrequencyencoded.HerebasedontheoriginalHodgkin-Huxleysystem，wesimplifyitsdifferentialequations;forfrequencyencoding，developsystemsdescribedbywithdecouplingtimescales;studydifferentmodesoffrequencyencodingariseasasingleparameterofthesystemisvaried.

Keywords:nervestimulation;frequencyencoding;Hodgkin-Huxleysystem;singularlyperturbedsystems;frequencymodulation

[收稿日期]2014-09-05

[中图分类号]O193

[文献标识码]A

[文章编号]1672-1454(2015)01-0014-07