粒子群算法课堂教学案例——求包含所有已知数据点的最小椭圆

戴　丽，　谢　政，　李建平

(国防科学技术大学理学院，湖南长沙410073)



粒子群算法课堂教学案例——求包含所有已知数据点的最小椭圆

戴丽，谢政，李建平

(国防科学技术大学理学院，湖南长沙410073)

[摘要]“现代优化方法”来源于各种大规模的工程实际问题的求解，也正是在工程实践问题的求解过程中得到不断发展。在该课程的教学中有必要引入案例。本文以粒子群算法为例，介绍本课程的一个教学案例：如何求包含所有已知数据点的最小椭圆。该案例在模式识别中有重要的应用.

[关键词]粒子群算法； 教学案例； 模式识别

1案例背景

美国Cleveland Heart Disease Database 提供了303个心脏病人的有关数据信息[1].该数据库记录了这些病人的血压(低压)、胆固醇等13项与心脏病有关的指标，同时，也记录了这些病人是否患有心脏病的确诊结论.现在的问题是如何根据这些数据对新来的病人只通过检查这13项指标，就推断该病人是否患有心脏病.该问题是病人患病确诊问题.本质上是分类问题，也称为模式识别问题.

假设只考察是否患有心脏病与人的血压(低压)[x]1和胆固醇[x]2这两项指标的关系.用“+”表示有心脏病，用“o”表示无心脏病.如果10个病人的数据如图1所示，则此时，可用一条直线(图中的粗线)将两部分数据分开.但当数据如图2所示时，则无法用一条直线将两部分数据分开，用一个椭圆(图中的粗线部分)区分两种数据.也就是说，此时，需要构造一个包括所有“o”型数据点的面积最小的椭圆.这是一非线性划分问题.

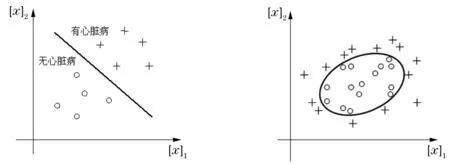
图1　用直线区分数据　　　　 图2　用椭圆区分数据

患病确诊问题是本文的应用之一.实际上，在模式识别问题中经常需要构造这样的椭圆.对于非线性划分问题，通常的做法是采用支持向量机，即构造核函数，并求解相应的二次规划问题.也可以借助于一些商业软件，如Halcon等解决该问题.本文则将现代优化算法应用于非线性划分问题，给出一个求面积最小椭圆的粒子群算法.该算法不需要构造核函数，也不需要函数的解析性质.因此，可广泛应用于问题的求解.

2问题的数学描述

以二维数据为例.如图3所示，设数据点所在的坐标系为xoy坐标系.设所求椭圆中心在xoy坐标系中为点(a，b).以椭圆的中心(a，b)为坐标原点，以椭圆对称轴为坐标轴，建立一个新坐标系XOY.XOY可由xoy经过旋转、平移得到.设旋转的角度为θ.设椭圆的两个半轴长分别为A和B.于是，所求椭圆在XOY坐标系中方程为标准方程

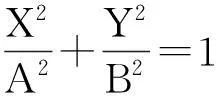
(1)

且

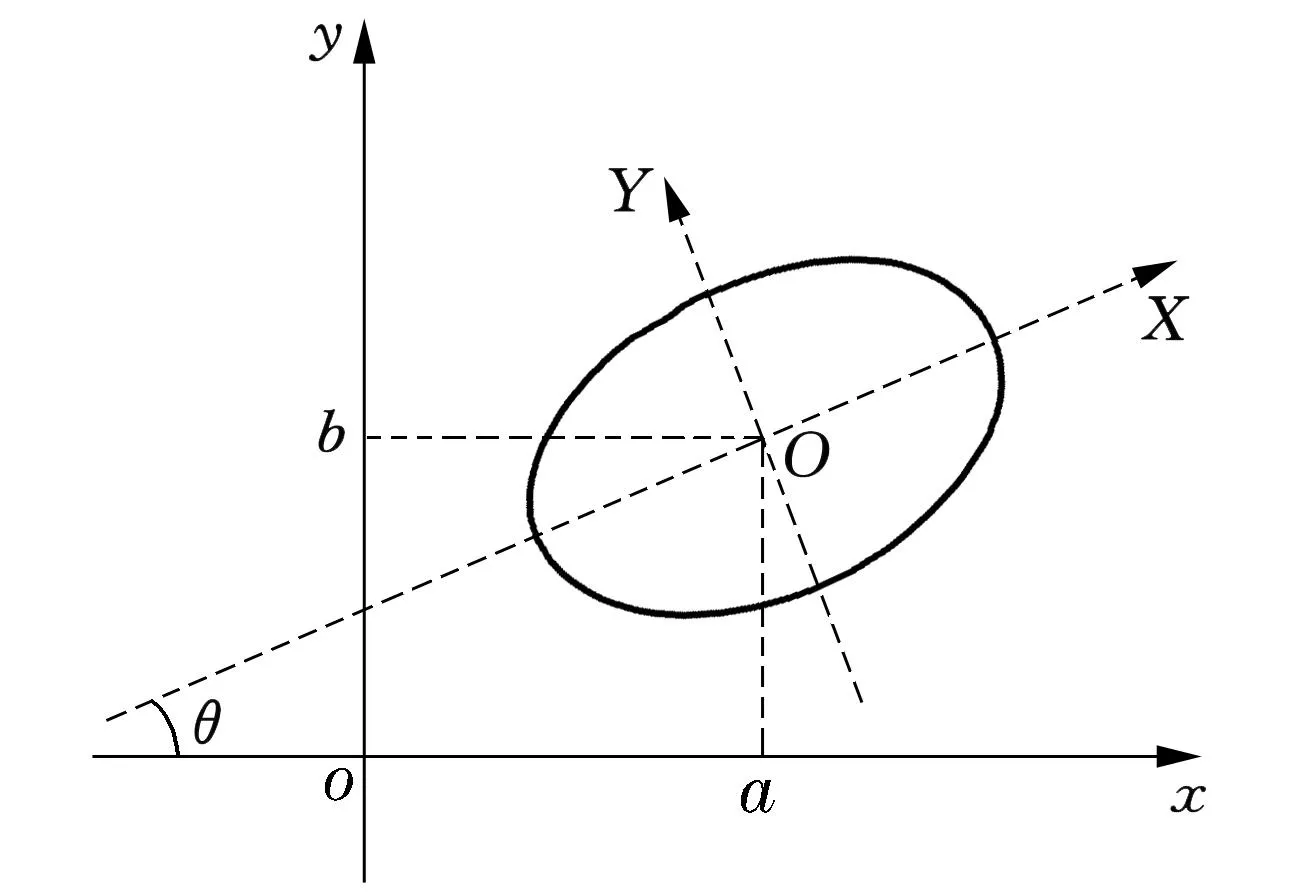
图3　坐标的建立及参数说明

(2)

由此可见，只要确定a，b，θ，A，B的值，椭圆的方程就相应确定.

要寻找一个包含所有已知数据点且面积最小的椭圆，每个已知数据点(x，y)代入(2)中得到的(X，Y)满足

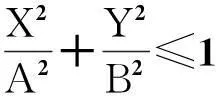
(3)

的前提条件下，使得椭圆的面积πAB尽可能小.

3粒子群算法求解问题

粒子群(Particle Swarm Optimization， PSO)算法是由Kennedy和Eberhart于1995年提出的.它与蚁群算法一样，也是通过模拟动物的群体行为来求解优化问题.PSO简单易行、收敛速度快、设置参数少，在各种优化问题中都有着良好的表现，其天然的实数编码特点使其尤其适合于处理实优化问题.PSO已成为现代优化方法领域研究的热点.

在PSO中，每个优化问题的解看作搜索空间中的一只鸟，称之为“粒子”.算法由多个随机产生的粒子(即随机解)组成的群体开始.每个粒子都被赋予一个由优化函数确定的适应值.每个粒子还有一个速度决定它们飞翔的方向和距离，然后粒子们就追随当前的最优粒子在解空间中搜索.在搜索时，每个粒子通过跟踪两个“极值”来进行位置(状态、也就是解)的变化，一个是粒子个体本身所找到的历史最优解，另一个是群体内(或邻域内)其他粒子的历史最优解，以使粒子能够飞向解空间，并在最优解处降落.

设第i个粒子的位置为：xi=(xi1，xi2，…，xin)；

第i个粒子的速度为：vi=(vi1，vi2，…，vin)；

第i个粒子经历过的历史最优解为：Pi=(pi1，pi2，…，pin)；

群体内(或邻域内)所有粒子所经历过的历史最优解为：Pg=(pg1，pg2，…，pgn).

一般来说，粒子的位置和速度都是在连续的实数空间内取值.在找到了两个“极值”后，每个粒子根据如下公式来更新自己的速度和位置：

vk+1=c0vk+c1ξ(pk-xk)+c2η(pg-xk)，

xk+1=xk+vk+1，

其中c1和c2称为学习因子或加速系数，一般为正常数.学习因子使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优解及群体内或邻域内的历史最优解靠近.c1和c2通常取为2.ξ和η是在[0，1]区间内均匀分布的伪随机数.c0称为惯性因子，其大小决定了粒子对当前速度继承的多少，合适的选择c0的值可以使粒子具有均衡的广域搜索能力(即探索能力)和局部搜索能力(即开发能力).粒子的速度被限制在一个最大速度Vmax的范围内.

下面介绍如何用PSO求解最小椭圆的构造问题.

3.1　个体编码

问题解的表达方式，称为编码方法，也就是将实际问题的解用一种便于算法操作的形式来描述.实际应用中，应当根据问题本身的特点和所使用的优化算法而采用不同的编码方法.在算法结束时，还需要通过解码还原到实际问题的解.由问题的数学描述可见，问题的关键在于合理确定

a，b，θ，A，B

的值.因此，本文采用五维向量(x1，x2，x3，x4，x5)表示粒子个体，各分量分别为a，b，θ，A，B的取值.

3.2　种群的初始化

由于粒子个体的不同分量表示椭圆的不同参数，因此，各分量应分别在其各自区域内初始化.

设xmin，xmax分别表示已知数据点的x轴分量的最小值、最大值；ymin，ymax分别表示已知数据点的y轴分量的最小值、最大值.粒子的第一个分量x1应初始化为区间[xmin，xmax]内的随机数，粒子的第二个分量x2应初始化为区间[ymin，ymax]内的随机数.粒子的第三个分量x3应在[0，2π)内取值.粒子的第四、五个分量x4，x5均在[0，D]内取值，其中D为数据点间的最大距离.当数据较大，计算所有数据点的最大距离比较困难，这时也可取D为最大数据点间距离的估计值.本文取

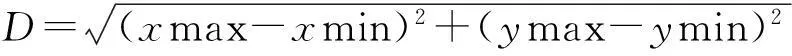
3.3　适应值函数

评价解的优劣的函数，称为适应值函数.实际应用中，对目标函数的任何变形都可作为适应值函数，但注意这个变形必须保证与原目标函数的大小顺序，即这个变形必须是严格单调的.适应值函数的确定原则是要便于算法的执行和算法效率的提高.

对于本文研究的问题，显然，当粒子个体满足条件(3)时，其适应值应为πAB；当粒子个体不满足条件(3)时，意味着该粒子个体不是问题的可行解，定义其适应值为+.粒子个体的适应值越小，说明粒子个体越优秀.

4仿真算例

4.1　实验数据

为了验证算法的有效性.我们以如下方式生成已知数据点.首先数据点中包含椭圆的四个顶点(也就是说，待求椭圆已确定)，然后在椭圆内随机生成其它的数据点.

设待求椭圆的中心为(2，2)；由xOy旋转45o得XOY坐标系；设其长、短半轴长分别为2，1.于是，其四个顶点分别为

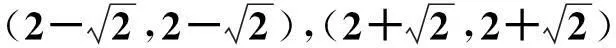
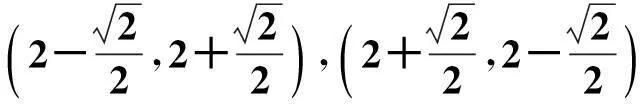
4.2　实验效果

算法中取惯性因子c0=0.1，两个学习因子c1=c2=2.种群规模N=100，迭代10000次.算法用6.346秒时间搜索到

椭圆中心(2.00109，1.9992)；旋转角度θ=0.764；

长半轴为2；短半轴为1.

如图4所示，从图中可以看出，算法得到了较理想的结果.

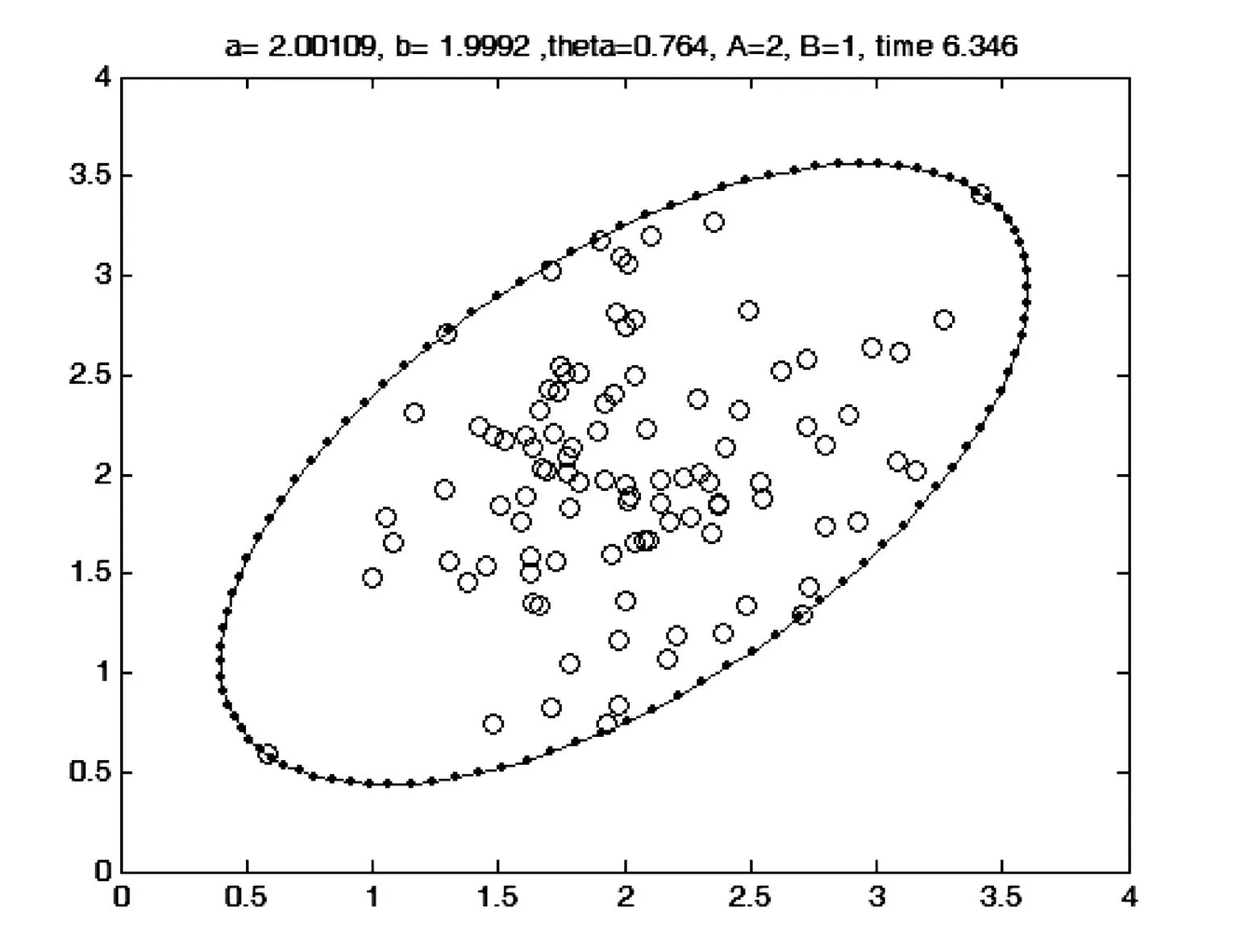
图4　实验效果

5推广

从仿真算法的实验效果可以看出，本文给出的算法不需要构造核函数，算法模型十分简洁，且效果理想.不仅如此，本文给出的算法模型可以推广到一般的n维空间.

5.1　n维数据分类问题的数学模型

在n维空间直角坐标系中，标准椭球方程为

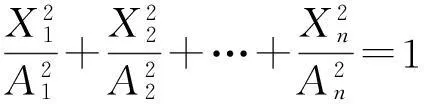
相应的“体积”与A1A2…An的值成正比.设H为n阶正交矩阵，b为一个n维列向量，设

X=H(x-b)，

(4)

于是，要寻找一个包含所有已知数据点且“体积”最小的椭圆，也就是要确定一个正交矩阵H，以及一个列向量b，在每个已知数据点(x，y)代入(4)中得到的X都有

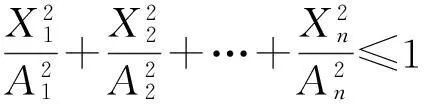
(5)

成立的前提条件下，使A1A2…An尽可能小.

5.2　仿真实验

以三维数据为例说明.随机生成测试数数点为

p1(-2.9604，0.8617，0.3232);

p2(0.9555，-0.0915，-0.0645);

p3(0.2321，1.5701，-2.5966);

p4(0.5161，1.3619，2.8822);

p5(1.0238，0.6885，-1.0355);

p6(0.5137，2.9083，1.3557);

p7(1.2563，-1.6493，2.4393);

p8(-2.0500，0.5274，1.6582);

p9(-1.2078，1.2676，-1.0486);

p10(0.0593，-1.0815，-2.6735).

这些数据点在三维空间中的分布如图5.

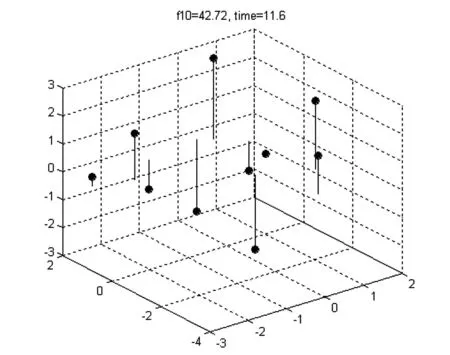
图5　测试数据点分布图

算法中取惯性因子c0=0.1，两个学习因子c1=c2=2.种群规模N=2000，迭代100次.历时 11.6秒搜索得到的正交矩阵H,b及A1，A2，A3分别为

b=(0.2506，-0.1123，-0.3651)，

(A1，A2，A3)=(2.6547，3.5119，4.5825)，

得到的椭球如图6所示.

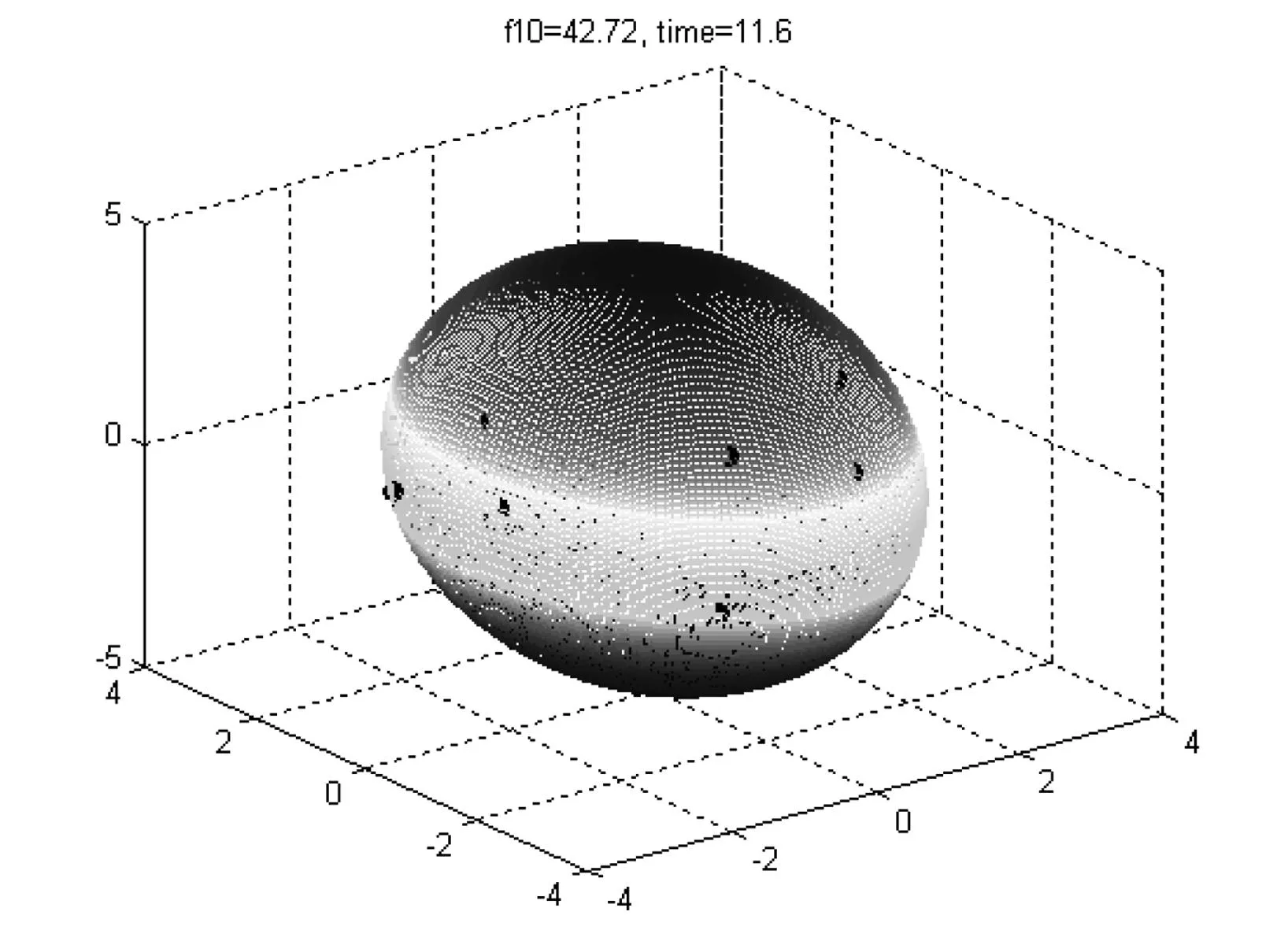
图6　三维数据时，算法搜索到的椭球

将上述算法得到的测试数据、H、b以及(A1，A2，A3)的值代入(5)式的左边，各点对应的值如表1所示.从表1中可以看出，p1，p4和p6这三个测试数据点对应的值都在0.95以上，已经很接近(5)式右边的1.这说明所得椭球的体积已经比较小，改进的余地已不大.

表1　效果分析

综合以上实验结果，可以发现，粒子群算法在11.6秒内即可得到较好的搜索效果.

6总结

文中以二维数据为例建模，说明了如何将本文给出的模型推广到三维、甚至其它高维空间中相应问题的求解.对二维数据的算法测试时，采用事先给定的数据，即待搜索椭圆是确定的，实验发现粒子算法可以很快找到这个确定的椭圆.在三维数据的测试中，我们则采用程序随机产生测试数据点，发现粒子群算法同样可以在很短的时间内找到一个体积较小的椭球包含所有已知的数据点.

总之，本文给出了一种用于求包含所有已知数据点的“面积”最小椭圆的粒子群算法.该算法模型十分简洁易懂，且搜索算法效果很理想.这也从一个侧面说明粒子群算法求解连续优化问题的强大能力.粒子群算法的优势在于简洁、高效.

值得指出的是，实际问题中的分类问题并非计算包含某一类别所有数据的最小椭圆.这是因为分类问题中的数据往往存在噪声，真正的分类问题需要将这些疑似噪声的数据排除在外，然后再构造这样的椭圆.

[参考文献]

[1]邓乃扬，田英杰.支持向量机-理论、算法与拓展[M].北京：科学出版社，2009.

[2]汪定伟，王俊伟，等.智能优化方法[M].北京：高等教育出版社，2007.

[3]Duds R O, Hart P E, Stork D G . Pattern Classification[M] . New York: John Wiley and Sons， 2001.

A Case Teaching PSO Algorithm

——to Construct the Least Ellipse Covering All the Datas

DAILi，XIEZheng，LIJian-ping

(College of Science， National University of Defense Technology， Changsha 410073， China)

Abstract:Modern optimize methods are rooted in solving large-scale projects， and tis rapidly progress is owed to solving the large-scale projects， too. It is necessarily to introduce case teaching for the class of modern methods. The paper provided a case which is about how to construct the least ellipse covering all datas using PSO algorithm. This case is widely used in the field of pattern identification.

Key words:PSO; case teaching; pattern identification

[收稿日期]2014-11-12

[中图分类号]TP18

[文献标识码]C

[文章编号]1672-1454(2015)01-0081-05