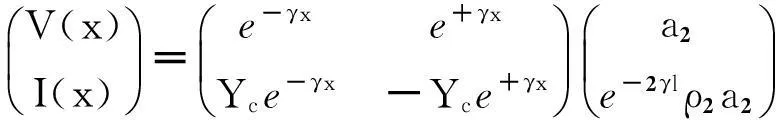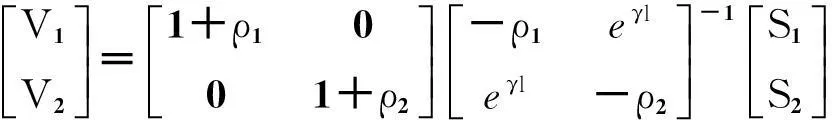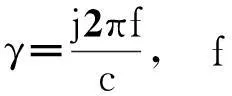常微分方程组求解的案例式教学探索

李　颖，　倪谷炎，　周　敏

(国防科学技术大学理学院数学与系统科学系，湖南长沙410073)



常微分方程组求解的案例式教学探索

李颖，倪谷炎，周敏

(国防科学技术大学理学院数学与系统科学系，湖南长沙410073)

[摘要]常微分方程在高等数学中占有很重要的地位，在该部分内容的教学过程中引入适当的教学案例，旨在激发学生学习常微分方程的热情和提高学生解决实际问题的能力.本文以传输线理论中的微分方程—电报方程求解为教学案例，在给出案例的研究背景和数学描述之后，求解电报方程获得了集总源激励下的传输线终端响应，并结合具体算例分析其物理意义.

[关键词]常微分方程； 案例式教学； 传输线响应

1案例背景

实践与应用是常微分方程的显著特点，在众多学科中都有应用常微分方程的方法和理论建立起来的数学模型，因此常微分方程的教学内容体现了多学科知识的交叉和渗透.这就要求教师在教学过程中不仅要使学生弄清楚常微分方程的一些基本理论和掌握各种类型方程的求解方法，还要让学生了解一些把实际问题归结为适当的数学模型的途径和方法，为他们今后运用数学知识解决实际问题打下坚实的基础.在介绍常微分方程类型以及解法时补充相关的一些科研成果，不但不会增加学生负担，反而会激发学生的学习兴趣，此外还反映了时代的气息，培养了学生的科研意识.从体系上来说，可以达到将单纯的知识结构转变成知识、思想方法和应用三位一体新知识结构的目的，从而起到素质培养、能力提高、技能训练为一体和谐发展的作用.我们将科研中集总源激励下的双导线传输线响应问题转化成高等数学课程教学过程中的具体案例，是对常微分方程案例式教学方式的一种有力尝试.

传输线理论是电磁兼容分析的重要理论，通常采用电报方程及相应的传输线耦合模型的形式来计算传输信号，其计算精度能够符合大多数工程应用的需要[1-2].一般情况下，传输线上的电压源和电流源可以产生天线模型和传输线模型两种响应.因此，传输线上的总电流分布就等于这两种模型共同的响应电流.但是，在很多电磁兼容分析中，对于只需要研究给定负载的终端响应情况时，计算传输线模型电流就已经足够了，因为天线模型电流在负载终端处消失[2].传输线集总激励是指传输线上某些位置有若干个原始激励源对传输线自身产生激励，这些离散的激励可以在整个线路里产生响应.下面几种情况均可以出现集总电压或电流激励现象：计算机系统中时钟发生器产生的噪声，计算机主板上高频数字信号和模拟信号之间的干扰，由系统中导体故障产生的短路以及在PCB板上静电放电产生的冲击[1].本文对集总源激励下双导线传输线的负载电流和电压响应进行研究，探讨其电报方程，即微分方程组的求解问题.

2案例的数学描述

对于集总源激励的均匀无限长双导体传输线而言，如图1所示，

图1　均匀无限长双导体传输线

其对应的电报方程[1]为

(1)

其中Z为单位长度阻抗，Y为单位长度导纳.由于是均匀传输线，传输线参数Z和Y与坐标位置无关.因此电报方程(1)实际上是一个常微分方程组.

3常微分方程组的求解

将微分方程组(1)去耦后可得到两个关于电压和电流的波动方程：

(2)

(3)

反向电压行波和电流行波分别为

该二阶微分方程组的通解因此可表示为两个方向的行波组合

(4)

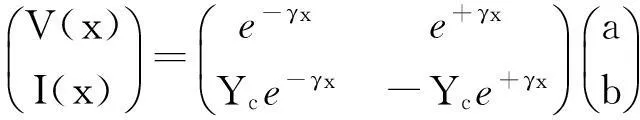
(5)

接下来探讨附加了边界条件的常微分方程组(1)求解问题.考虑集总电压源和电流源激励下的均匀有限长双导体传输线，如图2所示，双导体传输线线长均为l，两端端接负载阻抗为ZL1，ZL2，传输线受到x=xs处的串联电压源V0和并联电流源I0的激励.即电报方程(1)附加了x=xs处的边界条件：电流不连续差为I0，电压不连续差为V0，以及传输线两端负载1和负载2处的边界条件：

V1=-ZL1I1，

V2=ZL2I2，

(6)

其中(6)式中的负号来自于定义沿线传播的电流为正.

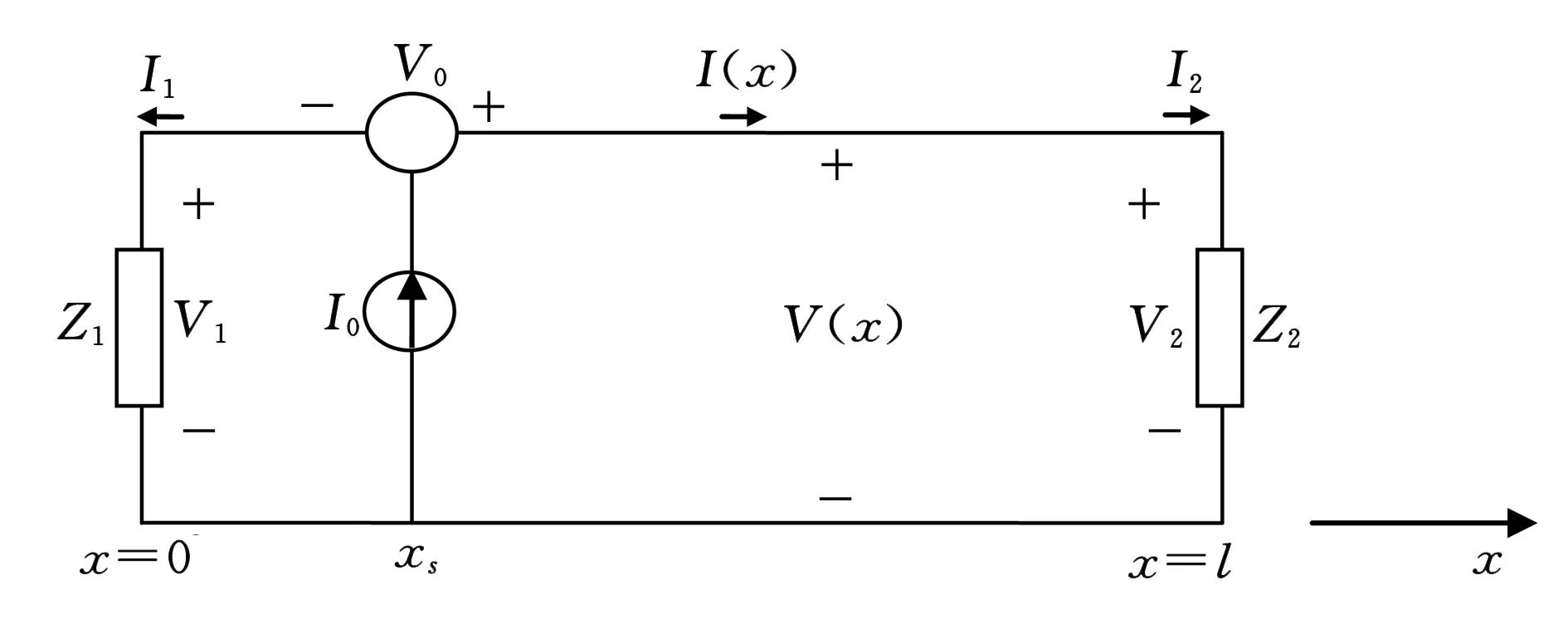
图2　任意集总源激励的有限长端接负载双导体传输线

设电报方程(1)的通解为

(7)

(8)

定义传输线终端负载的电压反射系数

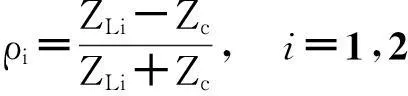
将其代入(6)再进而代入(7)和(8)中，可得a1=ρ1b1，b2=a2ρ2e-2γl.再结合x=xs处的边界条件，可得

(9)

(10)

于是，求得带两个边界条件的电报方程(1)的一般解为

(i) x

(11)

(ii) x>xs

(12)

在(11)和(12)中分别令x=0和x=l，可得传输线两个负载终端上的响应电压和电流为

(13)

(14)

注1上述电压和电流是线电压和电流，x=0处负载电流为线电流的负值，x=l处负载电流等于线电流，仍以I1表示x=0处的电流响应.

注2将传输线负载处的电压和电流响应改写成另一种矩阵形式

(15)

(16)

其中S1=eγxs(V0+ZcI0)/2，S2=-eγ(l-xs)(V0-ZcI0)/2.方程(15)和(16)即为BLT方程[1].

注3BLT方程最早由Baum，Liu和Tesche三人基于经典均匀传输线方程推导出来的经典方程[3]，并逐渐发展成为解决强电磁环境下复杂系统的电磁干扰与耦合问题的方法.该方程是求解传输线响应的紧凑矩阵形式，便于编程，易于推广.在系统电磁兼容分析与电磁干扰研究方面有着广泛的应用[4].

4数值仿真算例

研究只有电压源激励下的传输线终端响应情况，其结构如图3所示.

图3　由集总电压源激励的双导体传输线

传输线长度l=9米，线半径a=0.1厘米，线间距d=0.5米，终端负载Z1=50欧姆，Z2=100欧姆，特性阻抗

自由空间介电常数ε0=8.85×10-12F/m，自由空间磁导率μ0=4π×10-7H/m，传播常数

情况1作用于xs=2.5米处的电压源为V0=1.利用微分方程组(1)在传输线终端的解——BLT方程(16)求得集总电压源激励的双导体传输线终端负载处的电流响应，如图4和图5所示.

图4　终端x=0处的负载电流响应　　　　　　　图5　终端x=9m处的负载电流响应

从图4和图5可以看出，电流波形发生了振荡现象，这是由于终端不匹配，在传输线中存在谐振造成的，它对应于负载上的反射波.

情况2作用于xs=2.5米处的电压源为双指数电磁脉冲

如图6所示.利用BLT方程的时域形式求得集总电压源激励的双导线传输线终端负载处的瞬态响应，如图7所示.

图6　双指数电磁脉冲波形　　　　　　　图7　终端x=9m处的负载电流瞬态响应

从图7可以看出，在x=9m处直到时刻t=2.1×10-8s才有响应，说明源信号到达终端有时延现象.在时刻t=5.1×10-8s形成第1个最强尖峰，对应从x=9m端的一个往返时间.

由此可知，BLT方程在分析传输线频域与时域响应时均具有计算简便又能得到准确的结果的优势.

5 总结

由于案例的作用旨在引起学生勇于实践，深入探索教学案例中的问题，激发学生的学习兴趣，提高学生解决实际问题的能力.因此在常微分方程的教学过程中引入案例是对传统课堂教学的有利补充，以期解决学生缺乏创造性的顽疾，同时对提高教师的授课效果，扩展学生的视野，激发学生的创造性的具有积极意义，是一种教学方式的有力尝试.

本文基于传输线理论结合数学建模和常微分方程求解知识，解决了集总源激励下双导体传输线的响应问题.首先给出了案例的研究背景以及数学描述.接下来，对双导线系统的电报方程求解，并针对电压源激励传输线时频响应进行数值仿真计算.教学案例中所获得的数值仿真结果可用于分析电磁干扰问题，从而为传输线干扰信号抑制提供技术指导.

[参考文献]

[1]Tesche F M， Ianoz M V and Karlsson T. EMC analysis methods and computational models[M]. New York: John Wiley & Sons， 1997.

[2]Ushida H. Fundamentals of coupled lines and multiwire antenns[M]. Japan， Sendi: Sasak Press， 1967.

[3]Baum C E， Liu T K， and Tesche F M. On the analysis of general multiconductor transmission-line networks[J]. Interaction Notes 350， 1978: 230-331.

[4]Parmantier J P， Alliot J C， Labaune G， and Degauque P. Electromagnetic coupling on complex systems: topological approach[J]. Interaction Notes 488， 1990:1-14.

Case Teaching Investigation of Solving Ordinary Differential Equations

LIYing，NIGu-yan，ZHOUMin

(College of Science， National University of Defense Technology， Changsha 410073， China)

Abstract:Ordinary differential equations play an extremely important role in advanced mathematics. The purpose of the introduction of appropriate teaching cases during the teaching process of advanced mathematic is to stimulate students’ enthusiasm to study ordinary differential equations and improve students’ ability to solve pratical problems. The solution of telegrapher’s equations in transmission line theory was taken for case study as a form of differential equations. After the research background and mathematical description of case are introduced, the terminal responses of the transmission line under lumped sources excitation is acquired by solving the telegrapher’s equations Moreover, their physical significance was analyzed with the adoption of computational examples.

Key words:ordinary differential equations; case teaching; response of the transmission line

[基金项目]公共基础数学系列研究生一流课程体系建设项目

[收稿日期]2014-04-28

[中图分类号]O13；G642.1

[文献标识码]C

[文章编号]1672-1454(2015)01-0097-05