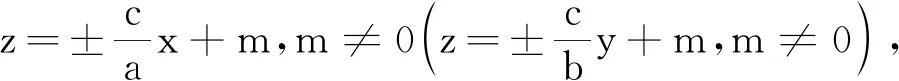二次曲面抛物截面存在性定理*
安佰玲,张德燕
(淮北师范大学数学科学学院,安徽 淮北 235000)
二次曲面是空间结构中最常见的函数曲面,在计算机辅助几何设计(CAGD)和机械制图中有重要应用.不少学者将二次曲面应用于研究参数曲面的拟合、复杂三维几何体的建模及曲面拼接问题[1-5],研究这些问题的过程中,都离不开二次曲面与平面的截线形状及参数方程的讨论.此外,讨论二次曲面上的具有某种几何特征的平面截线存在性问题,对于研究二次曲面的几何性质与形状具有重要的理论价值.目前,关于二次曲面平面截线的存在性及其应用研究大多集中在圆或椭圆截线上[6-9],因为这类二次曲线的代数方程比较容易构造.而关于抛物线截面的存在性及其代数方程求解问题的研究成果不多,因此,笔者拟利用2种方法给出二次曲面抛物线截面存在的条件及其代数形式.
1 预备知识
为了叙述方便,作以下约定:
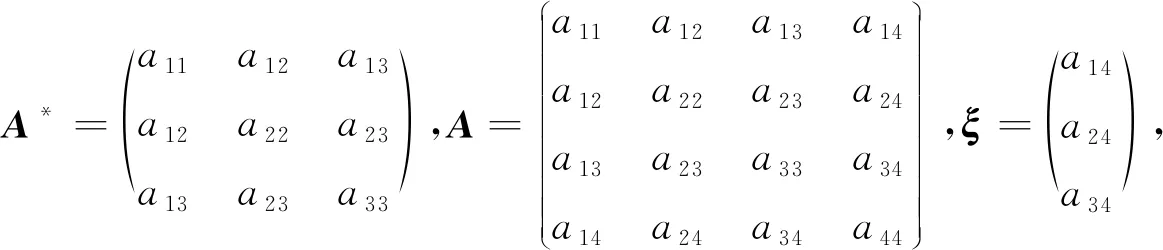
定义1设二次曲面S:F(x,y,z)=0,若平面π:lx+my+nz+p=0与S的交线为抛物线,则称平面π为二次曲面S的抛物截面.
引理1[10]对于二次曲面S:F(x,y,z)=0,设λ1,λ2,λ3为实对称矩阵A*的特征值,则存正交变换X=QY,使得S的方程变为
f(x′,y′,z′)=λ1x′2+λ2y′2+λ3z′2+ax′+b′y+cz′+d=0,
其中X=(x,y,z)T,Y=(x′,y′,z′)T,(a,b,c)T=2QTξ,d=a44.
二次曲面Σ:f(x′,y′,z′)=0与S:F(x,y,z)=0仅相差一个正交变换X=QY,因此二次曲面S抛物截面的求解可转化二次曲面Σ抛物截面的求解,所求的抛物截面也相差一个正交变换X=QY.
引理2[11]在xoy平面上,二次曲线φ(x,y)=0为抛物线⟺I2=0,I3≠0.
2 主要结果及其证明
定理1对于二次曲面Σ:f(x,y,z)=0,若二次曲面Σ存在抛物截面,设α,β为抛物截面上的正交单位向量,β沿抛物线的对称轴方向,则λ1,λ2,λ3不能同时为正或者同时为负,且:
(1)λ1,λ2,λ3均不为0且非同号(不妨设λ1λ2>0,其他情形同理可得).
①当λ1=λ2时,
其中θ∈[0,2π).
②当λ1≠λ2时,
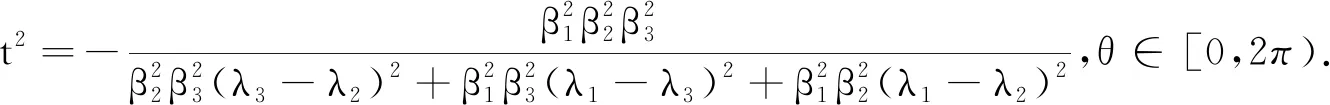
(2)λ1,λ2,λ3中有1个为0且其余2个同号(不妨设λ3=0,其他情形同理可得).此时,
α=(cosθ,sinθ,0),β=(0,0,1),
其中θ∈[0,2π).
(3)λ1,λ2,λ3中有1个为0且其余2个异号(不妨设λ3=0,其他情形同理可得).此时,
①β2=0,α=(cosθ,sinθ,0),其中θ∈[0,2π).

(4)λ1,λ2,λ3中有2个为0(不妨设λ1=λ2=0,其他情形同理可得).此时,
其中|m|≤1,θ∈[0,2π).
证明设二次曲面
Σ:f(x,y,z)=λ1x2+λ2y2+λ3z2+ax+by+cz+d=0,
(1)
平面π与曲面Σ交于抛物线Γ,P0(x0,y0,z0)为抛物线的顶点,α=(α1,α2,α3),β=(β1,β2,β3),由题意可得抛物线的参数方程为
(2)
其中t∈R,λ为不等于0的常数.将方程组(2)代入(1)式,可得
若二次曲面Σ存在抛物截面,则存在P0(x0,y0,z0)∈Σ,α,β,使得方程F(t)=0有无穷多解,结合α,β的几何特征,可得
(3)
及
(4)
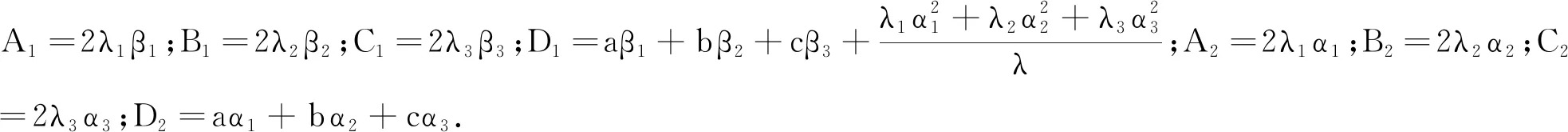
若Σ存在抛物截面π,则必然存在α,β满足方程组(3),显然λ1,λ2,λ3均不为0且同号时,方程组(3)中的第1个方程无解,因此二次曲面Σ无抛物截面.
(1)λ1,λ2,λ3均不为0且非同号时,不妨设λ1λ2>0.由方程组
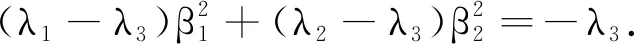
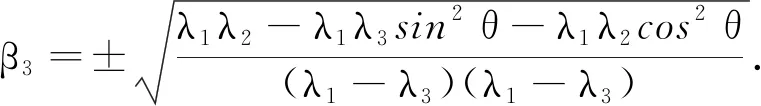
可得α1β1∶α2β2∶α3β3=(λ2-λ3)∶(λ3-λ1)∶(λ1-λ2).
①若λ1=λ2,由于β3≠0,否则β1=β2=0,于是α3=0,可得
其中θ∈[0,2π).
②若λ1≠λ2,由βi≠0,i=1,2,3,可得
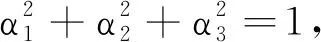
(2)λ1,λ2,λ3中有1个为0且其余2个同号时,不妨设λ3=0.由方程组
可得β1=β2=0,β3=±1.再由方程组
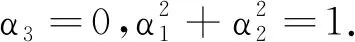
(3)λ1,λ2,λ3中有1个为0且其余2个异号时,不妨设λ3=0.由方程组
可得
①若β2=0,则β1=0,β3=±1,α=(cosθ,sinθ,0),θ∈[0,2π).
②若β2≠0,则β1≠0,由λ1α1β1+λ2α2β2=0,可得

(4)λ1,λ2,λ3中有2个为0时,不妨设λ1=λ2=0.将λ1,λ2代入(3)式,可得β3=0.由方程组

根据定理1,可得二次曲面Σ:f(x,y,z)=0抛物截面存在的必要条件,以及抛物截面法向量n=α×β必须满足的解析条件,但即使λ1,λ2,λ3,n满足定理1中的条件,其对应的平面也未必是Σ的抛物截面,还取决于方程组(4)的解的存在情况.
由定理1可得以下结果:
推论1设二次曲面Σ:f(x,y,z)=0,若λ1,λ2,λ3不同时为正或者同时为负,对于任意满足定理1中条件的α,β,存在λ≠0使得方程组(4)有解,则二次曲面Σ存在法向量为n=α×β的抛物截面,其抛物线的参数方程如方程组(2)所示.
除了利用抛物线的参数方程探求二次曲面抛物截面存在的解析条件,还可以结合抛物线在坐标面上的投影方程及其不变量给出解析条件.利用这种方法容易判别二次曲面是否具有平行于坐标面或坐标轴的抛物截面.
定理2平面π:lx+my+nz+p=0(n≠0)与二次曲面Σ:f(x,y,z)=0交于抛物线

(5)
的充要条件是
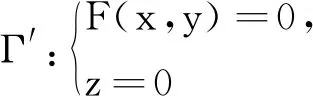
证明令
(6)
将方程组(6)代入方程组(5),可得

显然,方程组(6)对应R3中一个仿射坐标变换.根据经典二次曲线理论[10],抛物线在仿射变换下仍然是抛物线.证毕.
定理3对于二次曲面Σ:f(x,y,z)=0,有:
(1)二次曲面Σ存在平行于坐标面的抛物截面的充要条件是λ1=0,a≠0或λ2=0,b≠0或λ3=0,c≠0.

(3)二次曲面Σ存在与z轴相交的抛物截面z=lx+my+p的充要条件是λ3(λ1m2+λ2l2)=-λ1λ2,并且
A11l2+A22m2+A33p2+2A12lm+2A13lp+2A23mp+2A14l+2A24m+2A34p+A44≠0,
(7)
其中A11=λ1c2+λ3b2,A22=λ3a2+λ1c2,A33=-4λ1λ2λ3,A12=-λ3ab,A13=2aλ2λ3,A23=2bλ1λ3,A14=acλ2,A24=bcλ1,A34=-2cλ1λ2,A44=λ2a2+λ1b2,均为常数.
证明(1)二次曲面Σ存在平行于坐标面的抛物截面(不妨设其为平行于xoy面的抛物截面z=k)的充要条件为存在k,使得
是抛物线.由定理2,Γk是抛物线当且仅当
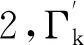
同理,二次曲面Σ存在平行于xoz面的抛物截面的充要条件为
λ1=0,λ3≠0,a≠0或λ3=0,λ1≠0,c≠0;
二次曲面Σ存在平行于yoz面的抛截面的充要条件为
λ2=0,λ3≠0,b≠0或λ3=0,λ2≠0,c≠0.
综上所述,二次曲面Σ存在平行于坐标面的抛物截面的充要条件为
λ1=0,a≠0或λ2=0,b≠0或λ3=0,c≠0.
(2)y=kx+m,k≠0是二次曲面Σ抛物截面的充要条件为存在k,m,使得
是抛物线.由定理2,Γk是抛物线当且仅当
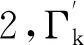
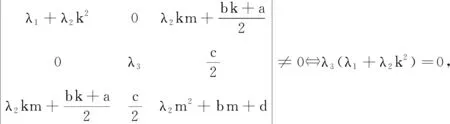

(3)z=lx+my+p是二次曲面Σ的抛物截面的充要条件为存在l,m,p,使得
是抛物线.由定理2,Γk是抛物线当且仅当
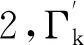
其中A11=λ1c2+λ3b2,A22=λ3a2+λ1c2,A33=-4λ1λ2λ3,A12=-λ3ab,A13=2aλ2λ3,A23=2bλ1λ3,A14=acλ2,A24=bcλ1,A34=-2cλ1λ2,A44=λ2a2+λ1b2,均为常数.证毕.
由定理3可得以下结果:
推论2二次曲面Σ:f(x,y,z)=0存在平行于坐标面的抛物截面的充要条件是λ1,λ2,λ3中至少有1个为0,并且为0的二次项对应变量的一次项不为0.
推论3对于二次曲面Σ:f(x,y,z)=0,有:
(1)若λ3=0,λ1λ2=0,c≠0或者λ3=0,c≠0,λ1λ2>0,则对于∀k≠0,m∈R,y=kx+m均为二次曲面的抛物截面.
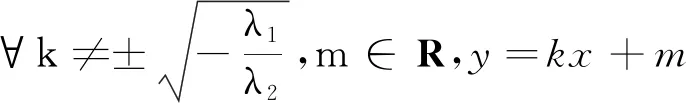
(3)若λ3≠0,λ1=λ2=0,则对于∀k(a+bk≠0),m∈R,y=kx+m均为二次曲面的抛物截面.
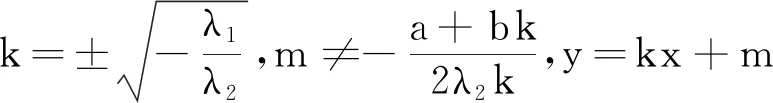
推论4对于二次曲面Σ:f(x,y,z)=0,有:
(1)若λ1=λ2=0,则对于∀l,m,p满足bl-am≠0,z=lx+my+p均为二次曲面的抛物截面.
(2)若λ3=λ1=0,a≠0,则对于∀l,m,p满足2cl+a≠0,z=lx+my+p均为二次曲面的抛物截面.
(3)若λ3=λ2=0,则对于∀l,m,p满足c2l2+(mc+b)2≠0,z=lx+my+p均为二次曲面的抛物截面.
(4)若λ1=0,λ2λ3≠0,a≠0,则对于∀l,m,p满足l=0,λ3m2+λ2≠0,z=lx+my+p均为二次曲面的抛物截面.
(5)若λ2=0,λ1λ3≠0,b≠0,则对于∀l,m,p满足m=0,λ3l2+λ1≠0,z=lx+my+p均为二次曲面的抛物截面.

3 5种典型二次曲面的抛物截面
5种典型二次曲面包括椭球面、单叶双曲面、双叶双曲面、椭圆抛物面和双曲抛物面,根据其标准方程、定理1、定理3及推论2~4,容易得到这5种典型二次曲面的抛物截面有以下结论(结论仅针对标准方程):
(1)椭球面不存在抛物截面.