关于n维正态分布线性函数服从正态分布的证明*

邢家省，杨义川，吴 桑

(1.北京航空航天大学数学与系统科学学院，北京 100191；2.北京航空航天大学数学、信息与行为教育部重点实验室，北京 100191)

n维正态分布及其线性函数在概率统计学中起到重要作用[1-16].n维正态分布的线性函数服从正态分布是一个经典结果，这个结果的证明方法通常有2种，一种是线性变换方法[15-16]，另一种是线性变换与特征函数相结合的方法[1-3].然而，这2种方法都涉及较多的知识，不方便掌握和使用.因此，笔者拟在已有研究成果的基础上，利用线性变换的传递性，给出n维正态分布的线性函数服从正态分布的一种直接的证明方法.

1 相互独立的正态分布随机变量的线性函数服从正态分布

利用正态分布概率密度的基本性质，可得正态随机变量的线性函数仍是正态随机变量，独立正态随机变量的和仍是正态随机变量，由此可进一步得到相互独立的正态随机变量的线性函数仍服从正态分布.

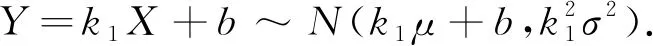
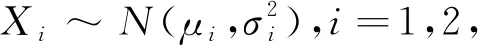
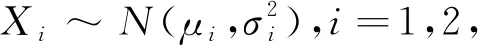
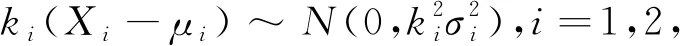
Z=k1X1+k2X2+b=k1(X1-μ1)+k2(X2-μ2)+(k1μ1+k2μ2+b)～

证毕.

利用引理3和数学归纳法，可将2个独立变量推广至多个独立变量，得到如下结果：

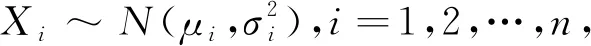
由引理4可知，相互独立的正态分布的线性函数服从正态分布.

2 n维正态分布的基本性质

设(X1,X2,…,Xn)是n维随机变量，若其概率密度

其中x=(x1,x2,…,xn)T,μ=(μ1,μ2,…,μn)T,Σ=(Cij)n×n是对称正定矩阵，则称(X1,X2,…,Xn)是n维正态随机变量[1-16]，或称(X1,X2,…,Xn)服从n维正态分布，记为X=(X1,X2,…,Xn)～Nn(μ,Σ).

下面介绍用雅可比行列式进行不同随机变量间线性变换的方法.雅可比行列式度量了单位立方体在应用映射时的体积变化量，可逆映射可以使用反映射的雅可比矩阵定义变换变量的概率密度函数，其具体变换公式如下：

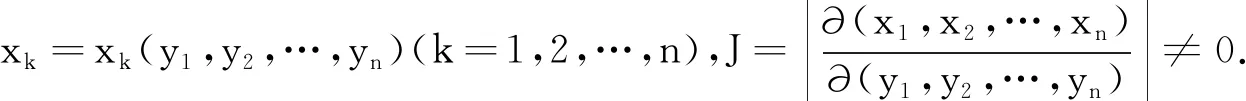
g(y1,y2,…,yn)=f(x1(y1,y2,…,yn),x2(y1,y2,…,yn),…,xn(y1,y2,…,yn))·|J|.

引理6[12-16]设X～Nn(μ，Σ)，A为n阶可逆矩阵，则有Y=AX～Nn(Aμ,AΣAT).

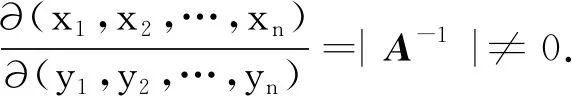
于是Y～Nn(Aμ,AΣAT).证毕.

由引理6可知，服从一般多维正态分布的随机变量在可逆矩阵线性变换下仍服从正态分布，由此可知可逆矩阵线性变换后的随机变量服从标准正态分布.

引理7[12-16]设(X1,X2,…,Xn)服从n维正态分布，则存在可逆矩阵B，使得

(U1,U2,…,Un)T=B-1((X1,X2,…,Xn)T-(μ1,μ2,…,μn)T)

服从n维标准正态分布.

证明设X=(X1,X2,…,Xn)T～Nn(μ,Σ)，其概率密度

因Σ是实对称正定矩阵，故存在可逆矩阵B，使得Σ=BBT，于是

B-1Σ(B-1)T=B-1(BBT)(B-1)T=(B-1B)(B-1B)T=In.

做变换U=B-1(X-μ)，利用条件X～Nn(μ,Σ)和引理6可得U～Nn(O,B-1Σ(B-1)T)，即U～Nn(O,In).因此，存在可逆矩阵B，使得U=B-1(X-μ)服从n维标准正态分布.证毕.

定理1设X=(X1,X2,…,Xn)T～Nn(μ,Σ)，且Σ=BBT，则存在相互独立且都服从标准正态分布的U1，U2，…,Un，使得

(X1,X2,…,Xn)T=B(U1,U2,…,Un)T+(μ1,μ2,…,μn)T.

由引理7，定理1得证.

利用定理1，可以证明X=(X1,X2,…,Xn)T服从n维正态分布的协方差矩阵

E((X-EX)(X-EX)T)=BBT=Σ.

定理1沟通了一般多维正态分布与多维标准正态分布的关系，也说明了多维正态分布的来源方式.利用定理1，可以研究多维正态分布的特征函数的计算公式和多维正态的性质.

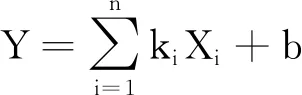
证明由定理1可知，存在可逆矩阵B，n维标准正态分布U，使得X=BU+μ.由于

Y=(k1,k2,…,kn)(X1,X2,…,Xn)T+b=(k1,k2,…,kn)B(U1,U2,…,Un)T+

定理2的证明是将定理1的结果代入，经过线性变换的传递表示为独立的正态分布的线性组合，即证明了n维正态分布的线性函数服从正态分布，这是一种简便、直接的证明方法.

3 n维正态分布的边沿分布服从正态分布

n维正态分布的边沿分布仍服从正态分布，所以服从n维正态分布的随机变量的线性组合可以是其各边沿分布的线性组合，问题可借助该思路进行讨论.

首先证明特殊的协方差矩阵下n维正态分布的边沿分布服从正态分布.

引理8[15-16]设X=(X1,X2,…,Xn)T～Nn(μ,Σ)，Σ>O，将矩阵剖分为

其中Σ11是r阶方阵.若Σ12=Σ21=O，则X(1)与X(2)相互独立，且X(i)～Nn(μ(i),Σii)，i=1,2.

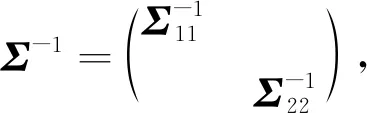
(1)

(1)式等号右端第1个方括号内是r维正态分布的密度函数，即X(1)～Nr(μ(1),Σ11)，同理X(2)～Nn-r(μ(2),Σ22).由于X的密度函数等于X(1)的密度函数与X(2)的密度函数的乘积，因此X(1)与X(2)相互独立.证毕.

下面将特殊的协方差阵推广至一般情况.

定理3[15-16]设X=(X1,X2,…,Xn)T～Nn(μ,Σ)，Σ>O，将矩阵剖分为

其中Σ11是r阶方阵，则有X(1)～Nr(μ(1),Σ11).

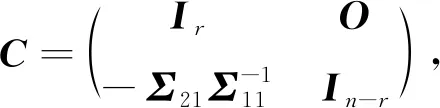
由引理8可得X(1)～Nr(μ(1),Σ11).证毕.

定理4[15-16]设X=(X1,X2,…,Xn)T～Nn(μ,Σ)，Σ>O，A为r×n阶矩阵，Rank(A)=r，b为r维列向量，则有Y=AX+b～Nn(Aμ+b,AΣAT).

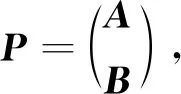
由引理6可知AX～Nr(Aμ,AΣAT)，AX为r维正态分布.由正态分布的期望与方差运算法则可知Y=AX+b～Nr(Aμ+b,AΣAT).证毕.

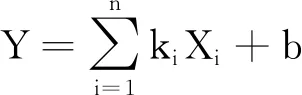
证明设A为非0行向量(k1,k2,…,kn)，这时Rank(A)=1，于是

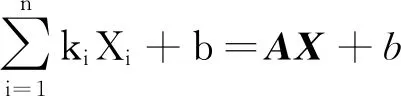
4 四维正态分布关于四阶矩的一个性质

利用多维正态分布的特征函数理论可讨论多维正态分布更多的性质[1-3,17-21].多维正态分布有各种不同的性质，其中四维正态分布有一个特别的关于四阶矩的性质.

定理5[3]设(X1,X2,X3,X4)服从四维正态分布，且EXk=0,k=1,2,3,4，则有

E(X1X2X3X4)=E(X1X2)E(X3X4)+E(X1X3)E(X2X4)+E(X1X4)E(X2X3).

证明由条件可知，Cij=cov(Xi,Xj)=E(XiXj),i,j=1,2,3,4.四维正态分布(X1,X2,X3,X4)的特征函数[1-3]

由矩与特征函数的关系可得

故结论得证.证毕.