新零售目标产品的精准需求分析与预测*

郎 红，常 啸，李 琴，宋国锋

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

目前，消费者对零售商品的需求逐渐增多，新零售企业逐步向商品多样化、小批量转变.但是，现有的零售行业库存管理方式不能快速适应这种生产模式.因此，分析零售商品销售量的影响因素及其作用效力，探究如何根据零售商品的销售和库存情况预测未来需求，合理安排库存并制定恰当的销售策略，是当前大多数新零售企业关注的问题[1].

对于商品需求的预测，学者大多选择综合指数法、Prophet-LSTM组合模型、灰色神经网络(Gray Neural Network, GNN)预测模型和BP神经网络模型等[2-5].其中灰色预测模型经过不断的发展，在少量和不规律样本的情况下能进行近期、短期和中长期预测，且在商品需求预测中不仅可考虑商品系统动态变化的随机性，也可考虑连续发展的变化过程[6].基于此，笔者拟选择灰色预测模型预测零售商品未来销售量和库存量.

1 数据来源与假设

本研究数据来源于赛氪官网赛题(https:∥www.saikr.com/c/nd/6456).为了方便研究，作出以下几点假设：

(H1)各零售商品销售方式不同.

(H2)对零售商品的销售量进行预测时，忽略社会各微观/宏观经济因素(如相关政策等)对销售的影响.

(H3)平均绝对百分比误差(Mean Absolute Percentage Error，MAPE，用M表示)能较好地反映零售商品销售量的预测误差程度.

2 精准零售销售量的影响因素分析

2.1 研究思路

笔者认为影响零售商品销售量的因素可分为销售方式和销售特征两大方面.为了验证此观点，笔者将针对这2个方面对2018年7月1日—10月1日累计销售额排名前50的零售商品单款单色(Stock Keeping Color，SKC)数据进行筛选，探究2018年国庆节(10月1日—10月7日)、“双十一”(11月11日)、“双十二”(12月12日)和元旦节(12月30日—1月1日)这4个节假日零售商品SKC销售量的影响因素及其作用效力.对于销售方式，设定不同的零售商品SKC代表不同的销售方式，通过单因素方差分析法进行研究；对于销售特征，选择库存、折扣、售价和标价这4个因素，先利用递归特征删除法筛选出影响程度较高的因素，再利用深层次回归分析法计算筛选出的各因素的调整拟合优度，并对各因素的影响程度进行比较.

2.2 研究方法

(1)单因素方差分析法.单因素方差分析[7]是指试验中只有1个影响试验指标的条件改变时，对试验数据进行分析，判断单个因素对试验指标的影响是否显著.设单因素A有r个水平，分别记为A1,A2,…,Ar，在每个水平下，需考察的指标被看作是一个总体Xi(i=1,2,…,r),Xi～N(μi,σ2)，样本在各水平下进行ni次独立检验，记作Xij(i=1,2,…,r;j=1,2,…,ni),Xij～N(ui,σ2)且相互独立.设定各零售商品销售量为参考数列(x0)，所属小类为比较数列(xi,i=1).

作以下假设：

(H4)u1=u2=…=ur.

(H5)μ1,μ2,…,μr不全相等.

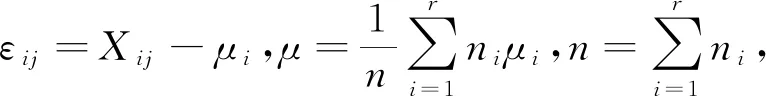
其中：i=1,2,…,r;j=1,2,…,ni；各个εij相互独立；μi和σ2未知.

(2)深层次回归分析法.递归特征删除法下，使用线性回归模型[8-9]，对所选择的库存、折扣、售价和标价这4个影响因素，每次删除1个因素进行回归；对得到的模型从均方根误差(Root Mean Squard Error，RMSE，用R表示)、调整拟合优度等方面衡量拟合效果，若拟合效果降低，则模型进行回滚删除操作，直至每个因素都被遍历.采用深层次回归分析法计算筛选出的各因素的调整拟合优度，在所有可能的子模型中添加1个预测变量引起的拟合优度平均增加量近似值，从而计算出每个自变量解释回归模型调整拟合优度，继而得到各因素的影响程度大小.

设各零售商品销售量为参考数列(x0)，库存、折扣、售价和标价为比较数列(xi,i=1,2,3,4)，对其进行递归特征删除法下的线性回归，模型为x0=β0+β1x1+…+β4x4+ε,ε为误差项.销售量分别取4个节假日的平均销售量，折扣分别取4个节假日的平均售价与标价的比值，库存分别取4个节假日首日和末日的库存量和的均值.

2.3 结果分析

(1)单因素方差分析法.利用SPSS软件对筛选出的数据集进行方差分析(Analysis of Variance，ANOVA)[10]，结果见表1.由表1可知，P=0.043<0.05，说明零售商品SKC的销售量具有统计学意义，即销售方式对零售商品SKC销售量具有显著影响.

表1 方差分析结果

(2)深层次回归分析法.利用R软件进行递归特征删除法下的线性回归，分析影响因素数量与模型RMSE的关系，结果如图1所示.由图1可见，当影响因素的数量调整为3时，模型的RMSE最小，拟合效果最好.

图1 变量个数与RMSE的关系

利用R软件进行递归特征删除，计算RMSE、相关系数(R2)、平均绝对误差(Mean Absolute Error，MAE，用A表示)及各自量纲化值(R-SD，R2-SD，A-SD)，结果见表2.由表2可知：标价的R-SD，R2-SD，A-SD最低，所以可删除该因素；库存和折扣对零售商品SKC销售量的影响较大，而售价的影响较小.

表2 递归特征删除结果

利用深层次回归分析法得到库存、折扣和售价这3个影响因素的调整拟合优度分别为88%，9%，3%，即3个因素对零售商品SKC销售量的影响从大到小排序为库存、折扣、售价，这与递归特征删除法得到的结果相同.根据库存这一因素的调整拟合优度为88%，可以认为零售商品的销售量与库存量之间存在很强的数量关系，新零售企业在预测零售商品库存量时可以借鉴销售量的预测方法.

3 灰色预测模型的销售量预测效果分析

3.1 研究思路

以目标小类27206656为例预测零售商品销售量.先以目标小类2019年6月4日—9月30日共17周各周的销售量作为样本数据，利用R软件进行灰色预测，得到目标小类10月1日—12月30日共13周各周的销售量预测值；再结合目标小类这13周的真实销售量和预测销售量，利用Excel软件计算各周的MAPE，分析模型的预测效果.

3.2 研究方法

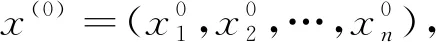
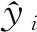
3.3 结果分析

对数据集进行筛选，得到目标小类2019年6月4日—9月30日共17周各周的销售量(表3).

表3 目标小类2019年6月4日—9月30日共17周各周的销售量

利用R软件对目标小类2019年10月1日—12月30日共13周各周销售量进行灰色预测，再利用Excel软件求解各周销售量MAPE，结果见表4.

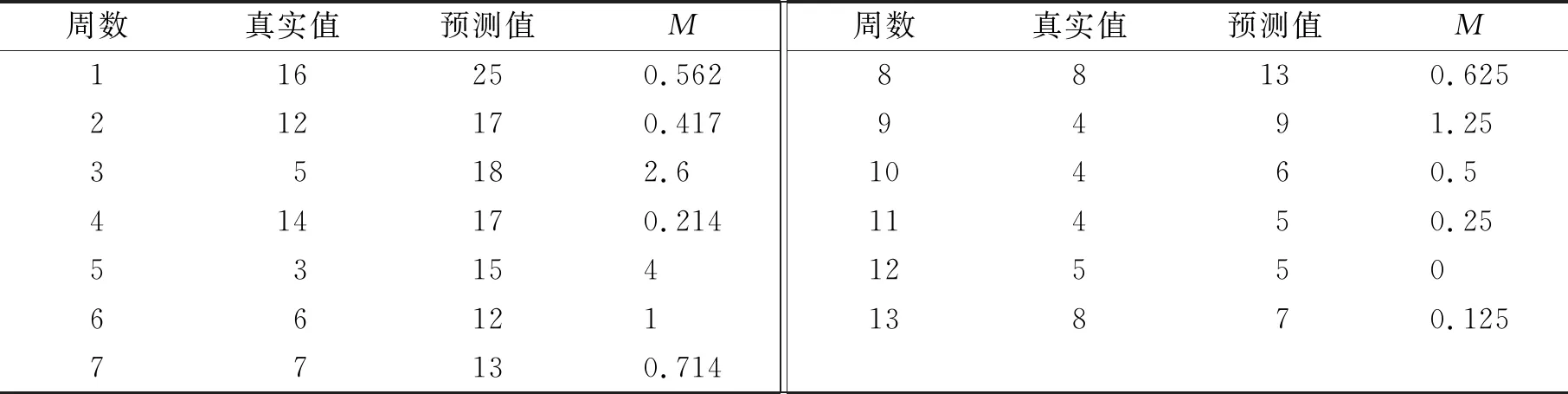
表4 目标小类2019年10月1日—12月30日共13周各周销售量真实值、预测值和MAPE

由表4可知，这13周中，目标小类的销售量真实值与预测值的MAPE大多小于1，最小为0.这说明，灰色预测模型可以较好地预测零售商品的销售量，模型的预测精度较高.

4 灰色预测模型的销售量和库存量预测应用

笔者继续以目标小类27206656为例，选取该小类2019年10月1日—12月30日共13周各周的销售量和库存量作为样本数据，利用灰色预测模型预测该小类未来的销售量和库存量.

利用Excel软件，筛选得到目标小类2019年10月1日—12月30日共13周各周的真实销售量和库存量(表5).

表5 目标小类2019年10月1日—12月30日共13周各周真实销售量和库存量

利用R软件对目标小类2019年12月31日—2020年3月31日共13周各周的销售量和库存量进行灰色预测，结果见表6.

表6 目标小类2019年12月31日—2020年3月31日共13周各周预测销售量和库存量

由表6可知，目标小类这13周各周的预测库存量远远大于预测销售量，说明存在明显的供大于求的现象.这提示新零售企业应及时根据顾客需求的变化调整该小类零售商品的采购计划(如控制进货量)，或者创新销售方式，增加零售商品销售量，从而减少库存管理成本.

5 结语

首先，利用SPSS软件、R软件，结合单因素方差分析法和深层次回归分析法研究了零售商品SKC销售量的影响因素及其作用效力；然后，以零售商品目标小类27206656为例，利用灰色预测模型预测了其销售量，并借助Excel软件验证得出预测模型的预测精度较高；最后，利用模型对该目标小类未来销售量和库存量进行了预测.笔者接下来将分析更多的零售商品销售量的影响因素及其作用效力，并考虑通过蚁群算法对灰色预测模型作改进，以进一步提高模型的预测精度.