蒙特卡洛算法在热防护服传热模型建立中的应用*

刘倩岚，雷亿辉，肖育江，董亚玲

(吉首大学数学与统计学院，湖南 吉首 416000)

在高温环境下，作业人员需要穿着特定的热防护服，以避免热源对人体造成的伤害，防止中暑、烧伤、灼伤等.因此，明确热防护服的导热规律、清楚高温环境中工作时间的极限，从而建立科学、准确的热防护服传热模型，制作出性能良好的专业防护服，可最大限度地保护作业人员的生命安全.学者对热防护服内部热量传递机理进行了研究，并建立了传热模型[1-6].但是，这些模型都需要求解微分方程，而在实际应用中，受边界条件的约束，微分方程的求解十分不易.于是，笔者拟通过蒙特卡洛算法求出温度分布模型中的相关参数，以提高建模效率.

1 防护服传热模型的建立

1.1 基于热传导原理的模型描述

本研究实验数据来源于2018年高教社杯全国大学生数模竞赛A题[7].将体内温度控制在37 ℃的假人放置在实验室的恒定高温环境中，研究高温环境下配备高温作业专用服装的人体皮肤表层的温度变化情况.

根据实验数据可知，导热过程中人体皮肤表层的温度随时间的变化而变化，且随着时间的推移逐渐趋于定值，由此可认为防护服的热传导是非周期性且非稳态的.基于此给出以下假设：

(H1)热防护服的纺织材料一、二、三层及空隙层分布均匀.

(H2)环境通过热防护服及空隙向假人导热是非周期性且非稳态的.

(H3)热量传播的过程只有传导没有对流.

(H4)热传递仅考虑热传导的影响，忽略汗液、水汽的影响，即不考虑湿传递.除热量传递外，忽略环境其他因素的影响.

热防护服的多层纺织面料导热，可转化为通过热防护服一维横截平板内的导热.在第3类边界条件下，由于热防护服的特征厚度很小，边界表面单位面积上的换热热阻远大于材料内部单位导热面积上的导热热阻，因此毕渥数Bi趋近于0，即

其中：d为材料层厚度；h为表面传热系数；λ为导热系数.进一步可知，在整个导热过程中横截平板各点的温度基本一致，即同一层的纺织面料质量与热容量都汇总到一点上，因此环境、热防护服、假人皮肤表层之间的导热分析可通过集中参数法进行.环境通过3层热防护服纺织材料，以及热防护服与人体间的空隙层(第Ⅳ层)将热量传递至假人皮肤表层(图1)，具体传热机制如下：(1)在初始时刻，热防护服3层材料温度相等，为 37 ℃，不进行热传导；进入高温环境后，热量先从环境传递至热防护服的第Ⅰ层，第Ⅰ层吸收热量而升温，再将热量传递至第Ⅱ层，以此类推，热量逐层传递.(2)置于高温环境时，每一层材料的属性不同，其吸收和放出的热量也不同.环境传递至第Ⅰ层的热量总大于第Ⅰ层传递至第Ⅱ层的热量，以此类推.由此可知，热量传递量是逐层递减的.(3)接触高温环境后，第Ⅰ层材料外侧流入热量，随着材料外侧温度升高，流入热量逐渐减少；同时，材料内侧温度梯度增加，流出热量逐渐增加，与流入热量差距减少；当流出热量等于流入热量时，传热进入新的稳态阶段，达到平衡.其他材料层以此类推.

图1 传热示意

由傅里叶导热定律可得材料的热流量计算公式为

(1)

其中：ΔΦ为导热热流量；ΔT为材料改变的温度；A为热传递面积.由(1)式可知，导热率增大时当层材料热流流量增加，因此降低材料的导热率，可有效提高防护服的隔热性能.

1.2 传热模型的建立

利用Matlab软件将5 400 s的实验数据转换为直观图形(图2).从图2可以看出，假人皮肤表层温度变化整体呈S型，变化趋势符合阻滞增长模型的特点.为了准确建立相应的阻滞增长模型，对温度变化数据进行具体分析：前15秒内，假人皮肤表层温度变化不明显；第16秒开始，假人皮肤表层温度迅速上升；第427秒后，假人皮肤表层温度上升速率由快变慢；第1 646秒后，假人皮肤表层温度趋于恒定，保持在48.08 ℃.

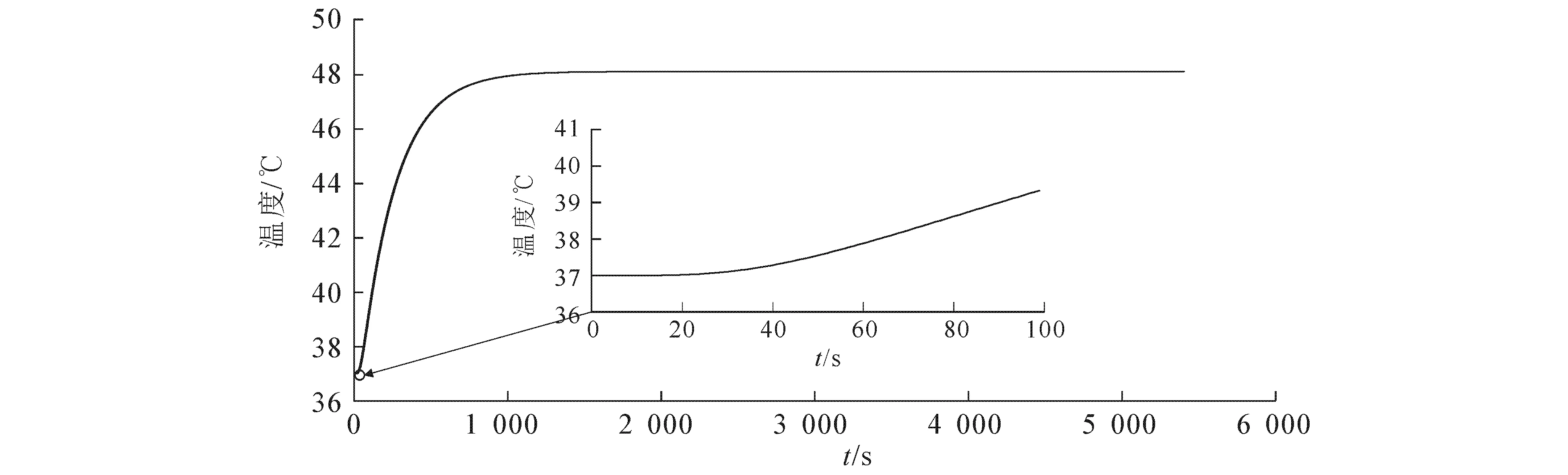
图2 0～5 400 s的假人皮肤表层温度变化

根据材料间热传导机制可知，每层材料当前温度T(t)等于前一刻温度T(t-1)与传入热量而升高的温度ΔT之和.ΔT的计算公式为

其中：ΔQ为热量传递量；c为材料的比热容；ρ为材料的密度.

热传导率表示单位截面和单位长度的材料在单位温差和单位时间内直接传导的热量.引入热传导率，可得各层材料的热量传递公式为

(2)

其中S表示材料的热传递面积.

由此，可以初步建立如下温度分布模型：

(3)

其中：T外为环境温度；Tj(t)为各层材料的当前温度；ΔTj(t)为每平方米各层材料改变的温度.

由于第Ⅳ层材料是空气，因此第Ⅳ层的温度函数可以近似为假人皮肤表层的温度函数.初始条件为 37 ℃的情况下，模型(3)的拟合数据曲线与实验数据曲线的对比结果如图3所示.

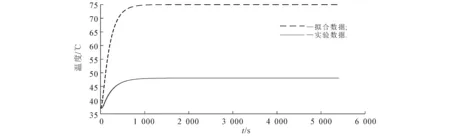
图3 初步拟合对比结果

从图3可以看出，当温度恒定时，由模型(3)得到的温度为75 ℃，远高于实验数据，且拟合曲线变化速率过快.由此可知，模型(3)拟合效果较差，需要对其进行修正.

1.3 模型的修正

考虑到人体散热机制、温差等因素对热传导的阻滞作用，对第Ⅳ层材料的温度函数引入阻滞因子.由于阻滞值不明确，温度函数的拟合效果不明显，因此在阻滞因子中进一步嵌入控制参数来调整阻滞作用.

(4)

为了提高控制参数α的计算效率，使得均方差达到最小，这里采用蒙特卡洛算法进行求解.蒙特卡洛算法也称为计算机随机模拟方法，是指使用随机数(或更常见的伪随机数)来解决计算问题的方法.设计蒙特卡洛方法的初衷是用于解决物理数值模拟问题，后来随着计算机的快速发展，这一方法广泛应用在函数值极小化、计算几何、组合计数等方面.如今，蒙特卡洛算法是求解科学、工程和科学技术领域大量应用问题的常用数值方法[8].利用蒙特卡洛算法进行求解，Matlab运行结果为α≈0.014 8.

2 模型检验

利用(2)式，可得每单位各层材料热传递到下一层同样单位的材料能够吸收的热量(表1).

表1各层材料吸收的热量

将ΔQj(j=1,2,3,4)，Ts，α代入模型(4)，可得假人皮肤表层温度的拟合值.模型(4)的拟合数据曲线与实验数据曲线的对比结果如图4所示，部分时刻拟合数据与实验数据的对比结果见表2.

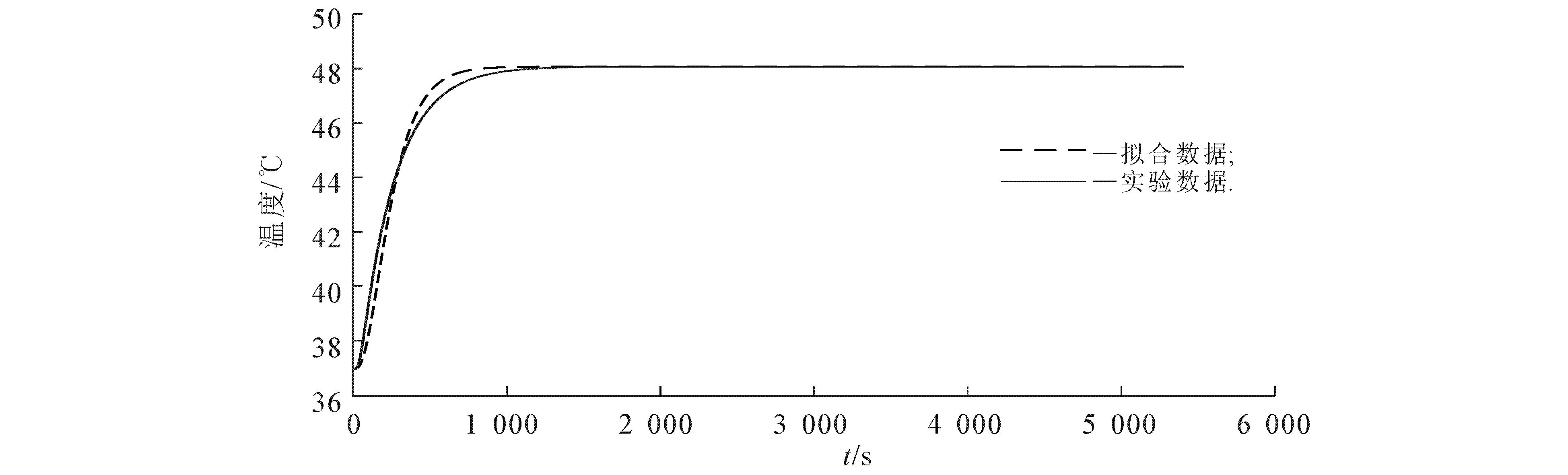
图4 修正后的拟合对比结果

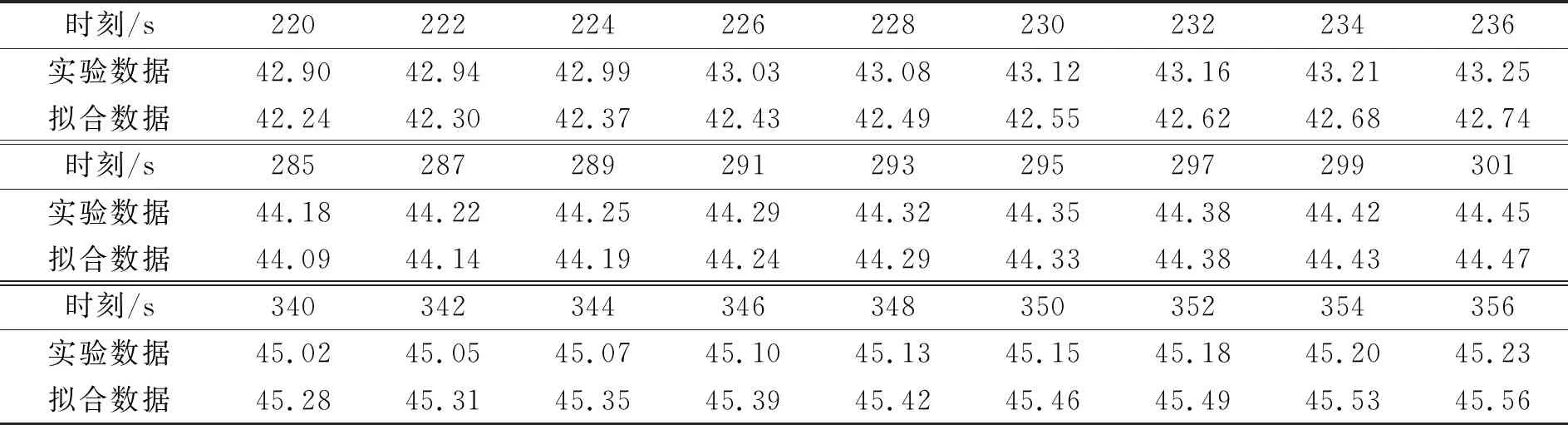
表2 部分时刻的拟合数据与实验数据的对比结果

从图4和表2可知，拟合数据与实验数据基本保持一致，说明模型(4)的拟合效果较好.拟合数据与实验数据有一定偏差的原因是，材料初始温度选取的是37 ℃，而现实环境中一开始材料温度并未达到37 ℃.尽管存在拟合偏差，通过模型(4)设计的热防护服依然能满足现实要求.这是因为，由图4可以看出，从第299秒开始拟合数据就略高于实验数据，表明基于模型(4)设计的热防护服实际达到的标准更高，即当热防护服在该模型下满足高温作业要求时，现实中也一定能满足防护要求.

3 结语

结合热传导原理和傅里叶定律分析了防护服传热机制及材料层温度、热量的变化情况，建立了初步温度分布模型.考虑到人体散热机制等因素对热传导的阻滞作用，引入含控制参数的阻滞因子来修正初步温度分布模型，并采用蒙特卡洛算法借助Matlab软件求解相关参数，得到修正温度分布模型.数值仿真实验结果表明，修正温度分布模型的拟合数据与实验数据基本保持一致，说明该模型的拟合效果较好.