平面体截交线边数和顶点数的计算模型研究
肖昕迪, 吴 燕
(安徽科技学院,安徽 凤阳 233100)
平面体截交线的绘制一直是建筑图学界的难题之一,需要从平面到三维空间反复模拟、求证后方得以解决。从截切体断面形状的空间想象,到其三面投影图中边数和顶点数的确定,以及最终投影图的绘制,每一步都错综复杂,其中截交线的边数和顶点数的确定是最关键的一步。目前解决平面体截交线投影图难题的常用方法为画法几何法求解截交线多边形[1],即先根据截切位置判断截交线的形状[2],以截切面与形体各棱线的交线为线索[3],在形体面上取点的方法[4],找出截交线各顶点的位置,按三视图的“三等”关系,画出截交线各顶点的三面投影,最终围合出截交线[5]。这种方法求截交线多边形,对空间想象能力要求高,截交线形状判断时需要花费时间建模空间形体。另外,因为截交线多边形的边数和顶点数不确定,画图过程中容易出现思路不清晰,导致三视图的轮廓线遗漏、多画现象,审核图样耗时较多。
为了快速判定平面体截交线的边数和顶点数,节省绘图的时间成本,提高画图的准确性,本文提出了构建平面体截交线的计算模型方法,求解出截交线多边形顶点数、边数,来确定整个截交线的形状,最终按照投影规律补全截切体的三视图。对此,深入分析由单截面到多截面的顶点和边数计算特点,建立截交线边数和顶点数建计算模型。
1 单截面平面体的截交线算法
单截面平面立体的截交线是一个由直线组成的平面封闭多边形,其形状取决于平面立体的形状及截平面在平面立体上的截切位置。目前常用的方法有两种:棱面法和棱线法。
1.1 棱面法
将参与相交的各棱线(或底边)与截平面求交线,交线的集合即为所求截交线[6]。截交线的边数可视为截平面所截到的棱面数。以图1为例,图中正四棱锥被倾斜的正垂面切割,四个侧棱面全被切到,就会有四段交线,这四条交线的集合即是此截交体的截交线(Ⅰ Ⅱ、Ⅱ Ⅲ、Ⅲ Ⅳ、Ⅳ Ⅰ),截交线的边数N总设定为:
N总=Ny
(1)
其中,N总为截交线的总边数;Ny为被截平面截到的棱面(或底面)数。
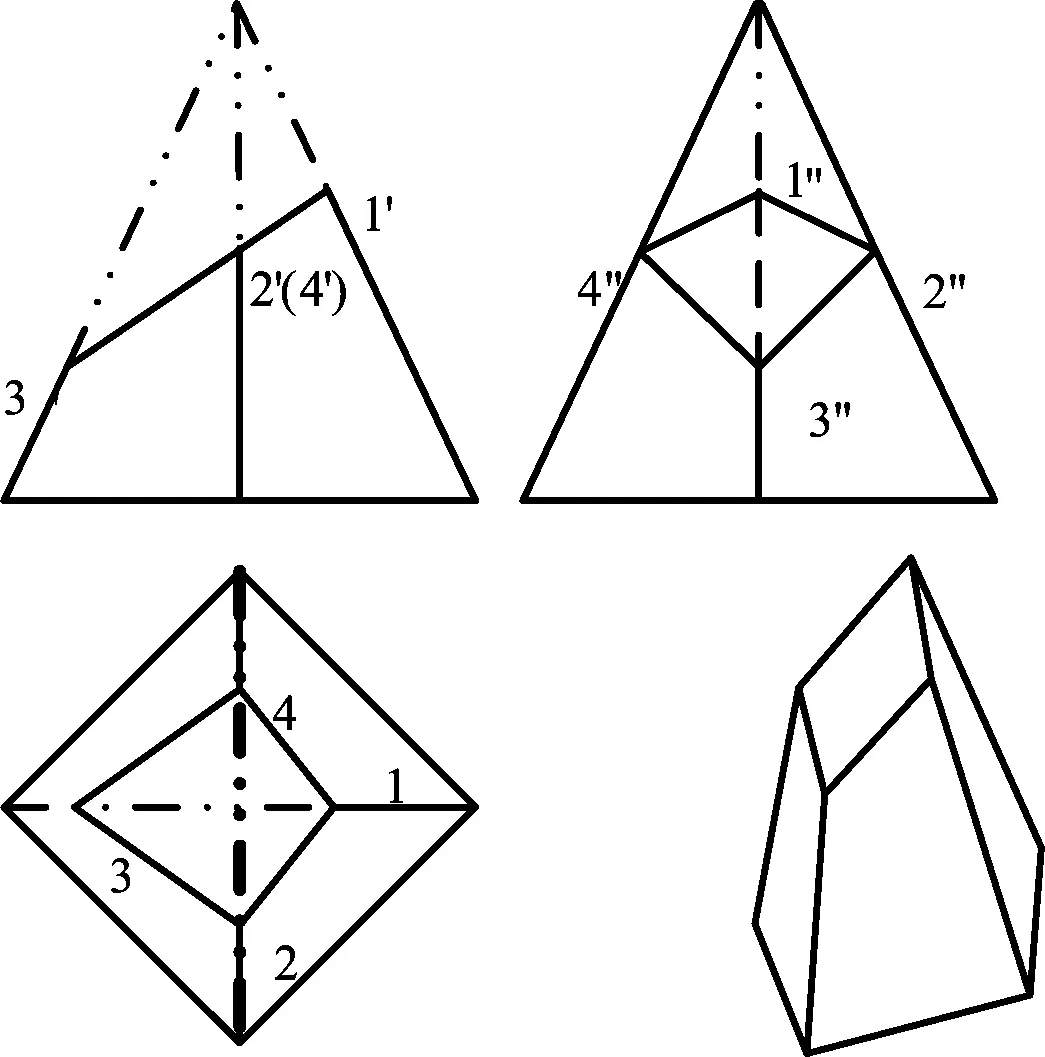
图1 一个平面截切四棱锥的截交线
1.2 棱线法
将参与相交的各棱线(或底边)与截平面求交点,然后将各交点按照位置关系依次连接,即为所求截交线[6]。此时,棱线(或底边)与截平面相交时产生的交点个数的即为截交线多边形的边数。如图1,正四棱锥被倾斜的正垂面切割,有4条棱侧棱全被切到,有4个交点(Ⅰ、Ⅱ、Ⅲ、Ⅳ)。计算式设为:
M总=Mx
(2)
其中,M总为截交线总定点数;Mx为被截平面截到的棱线(或底边)数。
单截面的平面体截交线,是最简单的截切情况,不适合直接计算2个或者2个以上的截面截切体的截交线边数和顶点数。
2 多截面平面体的截交线边数和顶点数计算模型的构建
2.1 多截面平面体截交线边数的计算模型
以图2为例,3棱锥被2个相交的截平面(水平面和倾斜于水平面的正垂面)截切时的截交线。若按照式(1)棱面法的算法:截交线的总边数应为两个截平面产生的截交线边数的总和,列式为:N总=N1+N2=3+3=6。
N1——第一个截平面截切时产生的截交线边数
N2——第二个截平面截切时产生的截交线边数
从空间图上可以数出截交线的总顶点数为6,分别是:Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ;总边数是7,不是6,分别为:直线ⅠⅡ,直线Ⅱ Ⅴ,直线Ⅴ Ⅵ,直线Ⅵ Ⅰ,直线Ⅱ Ⅲ,直线Ⅲ Ⅳ,直线Ⅳ Ⅴ,在采用式(2)累加的基础上需要再加数字“1”。“1”来源于2个截平面不是各自独立地作用平面体,截平面之间有1条交线。由此设置代表交线数量的参数X。
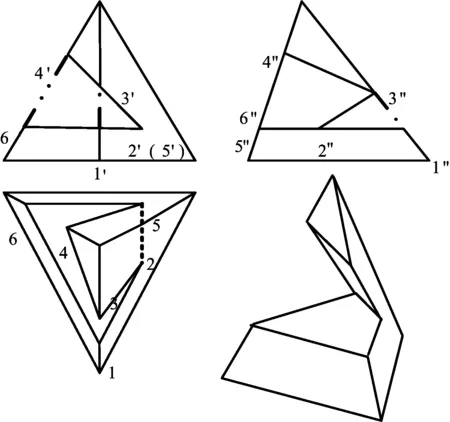
图2 两个平面截切三棱锥的截交线
由此,计算图2形体截交线边数的时,分别计算2个截平面独立截切时各自产生的截交线边数,在此基础上加上截平面之间相交的交线数参数,即可算出截交线的边数。过程如下:
先按照式(2)的计算方法可得:N1=3,N2=3;再加上交线数参数。列式为:N总=3+3+1=7。与空间图形中的截交线的边数一致。
由此,构建多个截切面形成截交线边数N总的计算模型为:
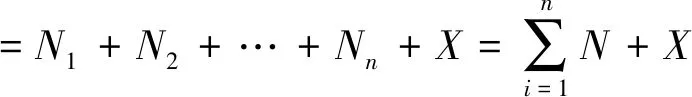
(3)
其中,N1为第一个截平面截切时产生的截交线边数;N2为第二个截平面截切时产生的截交线边数;Nn为第n个截平面截切时产生的截交线边数;X为截平面之间的交线数。
2.2 多截面平面体截交线顶点数的计算模型
仍以图2中的平面形体为例,设顶点数为M总。有两个截平面作用平面形体,每个截平面切到2个棱,按单个截平面形成的截交线顶点数的两次累加,M总=4,和空间截交线6个顶点数并不一致,需要加上截平面之间相交交线的2个端点。因此,需要设置截平面之间交线的端点数参数Y,因每条交线有2个端点,故Y=2X,X为截平面之间的交线数。图2中截交线的顶点数计算式可列为:M=M1+M2+Y=2+2+2=6,与空间图形中的截交线的顶点数一致。
由此,构建多个截切面形成截交线顶点数的计算模型为:
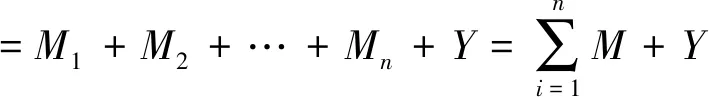
(4)
其中,M1为第1个截平面截到的棱线数;M2为第2个截平面形成的棱线数;Mn为第n个截平面形成的棱线数;Y为截平面之间交线的端点数。
2.3 模型对单截面的适用性
式(3)(4)是以多个截平面截切平面形体为模型建立的,对于1个截平面截切平面形体所形成截交线的计算也可以使用(3)(4)式,二式中的Nn、X、Mn、Y都没有值,或者都设为零。因此,1个截平面的情况也适用。
3 截交线边数和顶点数计算模型的验证
3.1 三个截平面作用的截切体
如图3所示,正四棱锥被水平面、铅垂面、正垂面3个截平面截切,3个截平面有2条交线,参数X=2,参数Y=4。
按式(1)(3)可得截交线的边数为:N总=N1+N2+N3+X=4+2+4+2=12;
按空间图和式(1)、(4)可得截交线的顶点数为:M总=M1+M2+M3+Y=3+0+3+2×2=10;
以上结果与空间相符。
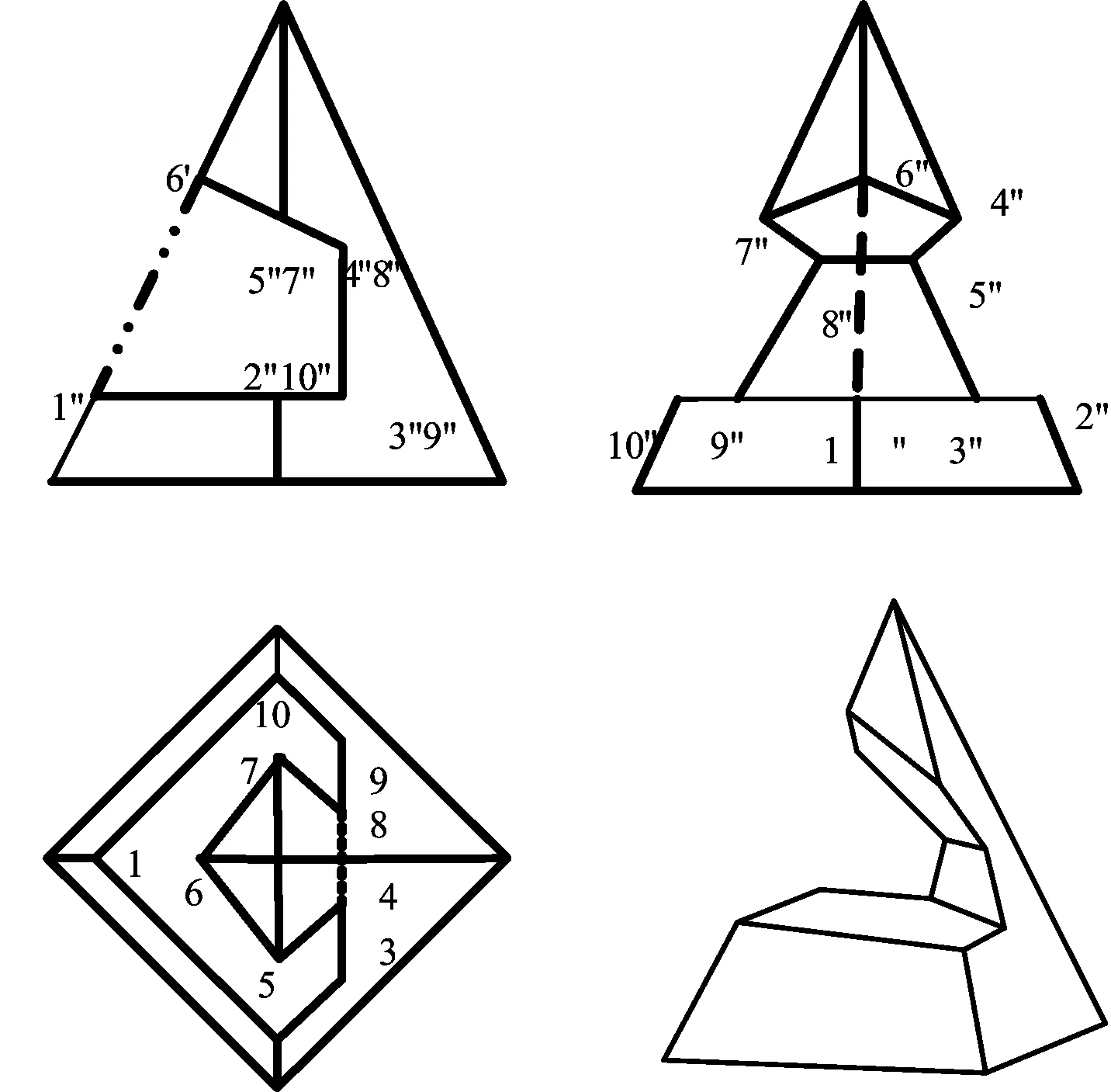
图3 三个平面截切四棱锥的截交线
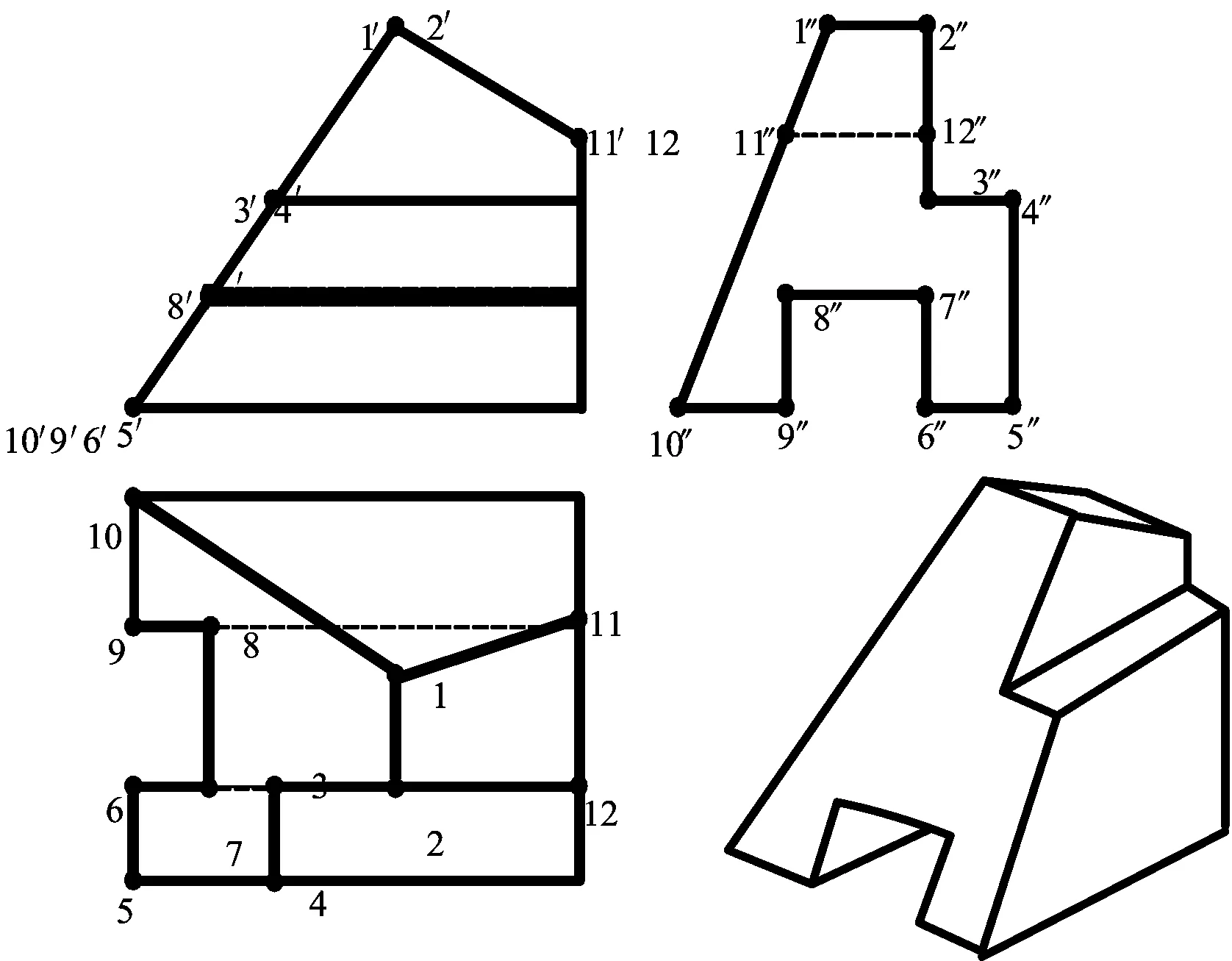
图4两个平面截切棱柱的截交线
Fig.4 Intersection line of two planes cutting prism
3.2 两个截平面作用的截切体
如图4所示,横放的棱柱被2个倾斜的正垂面截切,有1条交线,参数X=1,参数Y=2。按照式(1)(3)(4)计算,可得截交线的边数为N总=13;截交线的顶点数为M总=12。结果与空间相符。
3.3 单截平面作用的截切体
如图5所示,水平放置的六棱柱1个倾斜于正面投影面和侧面投影面的铅锤截平面截切,截切到6条棱线和6个棱面,截交线的边数和顶点数均为6,按式(3)(4)计算N1=6,M1=6,其余参数和变量都为0,截交线的边数:N总=N1=6。
截交线的顶点数为:M总=M1=6,结果与空间相符。
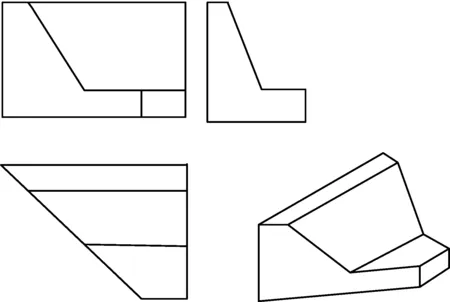
图5 一个截平面截切棱柱的截交线
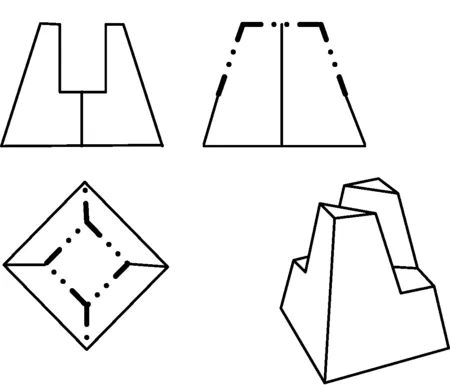
图6三个平面截切四棱台的截交线
Fig.6 Intersection line of three planes cutting four prism
4 截交线边数和顶点数计算模型的应用
如图6所示,为被3个截平面(2个侧平面和1个水平面)截切的四棱台,求其被截切后的截交线。
解题思路:先把截交线的顶点数和边数分别用式(3)(4)计算出来;再按照求出的边数和顶点数利用投影规律来连接围合成各投影面上截交线投影。
4.1 先求解出截交线的边数和顶点数
空间分析:水平截平面与四棱台4个棱面相交,交于4条边,即N1=4;2个侧平截平面均与四棱台3个面相交,分别交于3条边即N2=3,N3=3;截平面之间有2条交线,即X=2。则此截交体截交线的边数N总=N1+N2+N3+X=4+3+3+2=12。
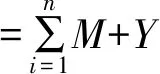
空间分析:水平截平面与四棱台两个棱相交,即M1=2;两个侧平截平面均与四棱台上底面分别两个棱相交,即M2=2,M3=2;截平面之间有2条交线,每根交线2两端点,即Y=2X=4。则此截交体截交线的边数M总=M1+M2+M3+Y=2+2+2+4=10。在正面视图中注出10个点的位置和编号。详见图7。
4.2 补齐各点的投影,连接围合成截交线
由上面的空间分析和顶点、边数计算得出,截交线是空间10边形,并有2条交线。按照三面投影“长对正、宽相等、高平齐”的作图规律[7-8]和形体表面点的投影规律,求解出10个点的另两面投影,并分别连接成截交线的各面投影,详见图8。
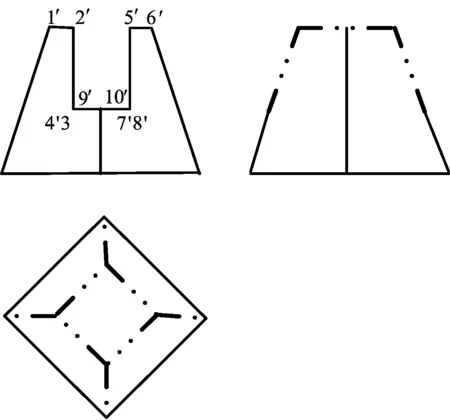
图7 三个平面截切四棱台的截交线
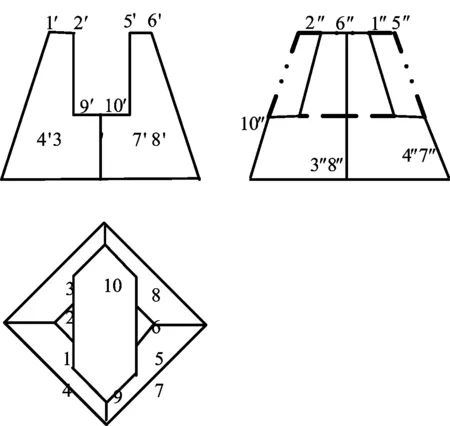
图8三个平面截切四棱台的截交线
Fig.8 Intersection line of three planes cutting four prism
5 结论与讨论
通过空间图形的验证表明,截交线顶点和边数的计算公式是可行的。通过设置截平面交线参数解决了多截面平面体的截交线边数和顶点数计算,通过截交面交线推出两个参数间的关系,解决了截交线求解过程中的边数计算难题。省去了对截交线复杂的空间想象和建模的时间,为工程中常见的平面形体截交线的求解提供了普适方法。
本文只讨论了平面体被一个或多个相交截平面截切时截交线边数和顶点情况,对于曲面体被截切时截交线的边数和顶点确定尚未讨论。式(1)和(2)只适用于平面体被一个截平面截切时对截交线边数和顶点的确定。式(3)和(4)适用于平面体被一个或多个截平面截切时对截交线边数和顶点的确定,是否适用于曲面形体、相贯体和组合体还有待进一步的研究。

