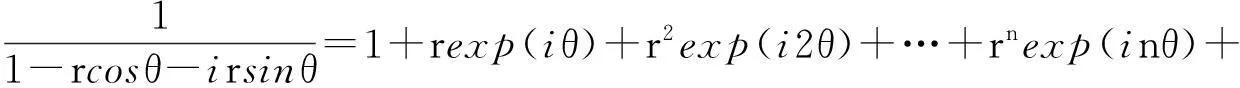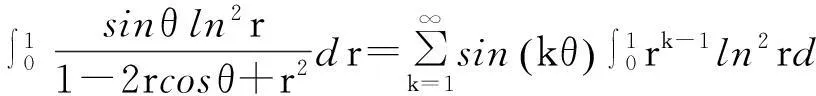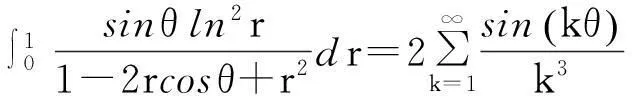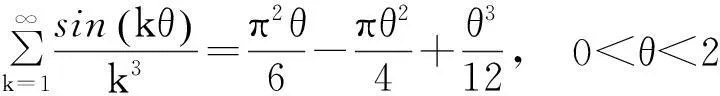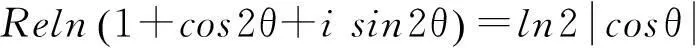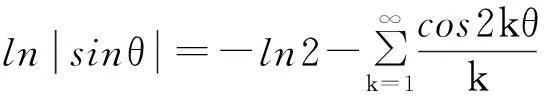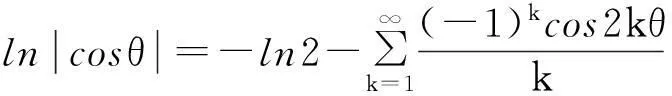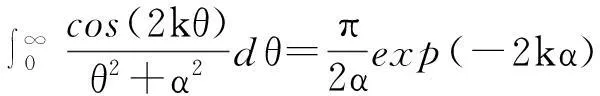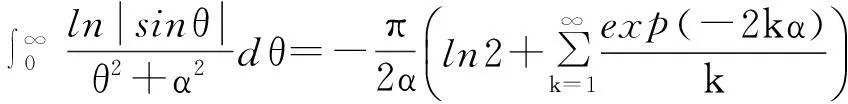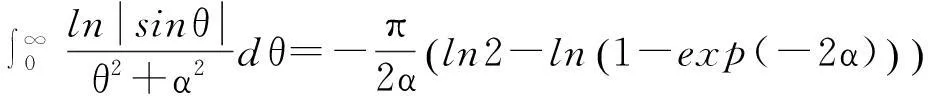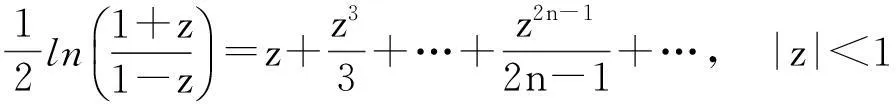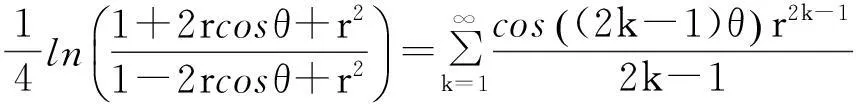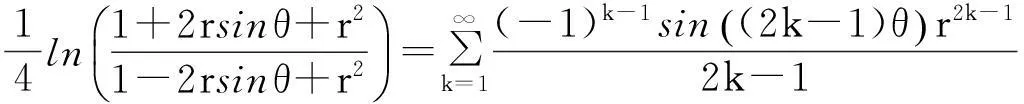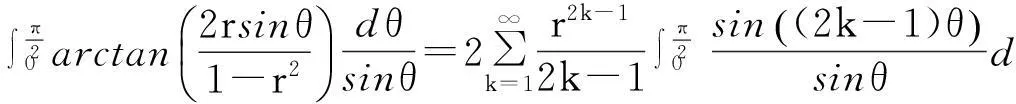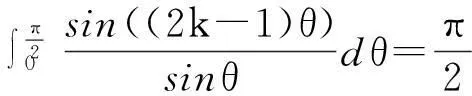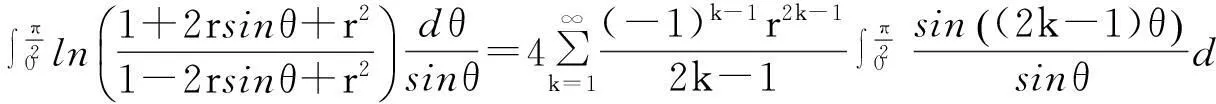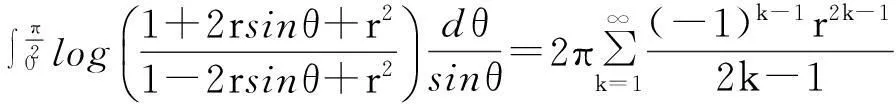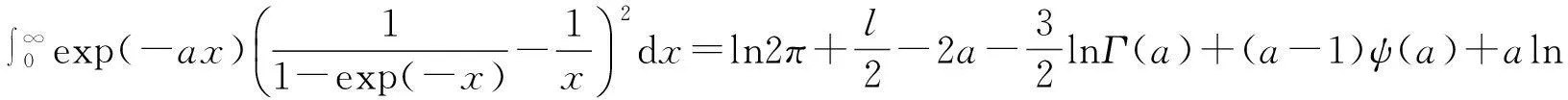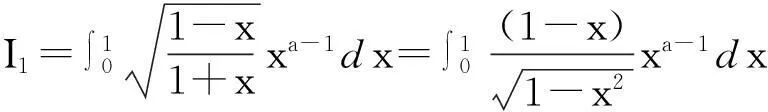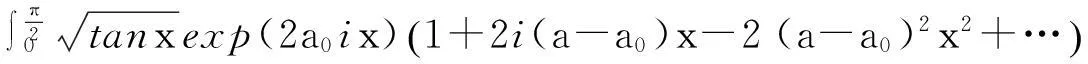定积分计算探讨

邱为钢

(湖州师范学院理学院, 浙江湖州313000)



定积分计算探讨

邱为钢

(湖州师范学院理学院, 浙江湖州313000)

[摘要]综合利用傅里叶级数法，参数求和法, 参数展开法, 得到了一些定积分的值.

[关键词]傅里叶级数; 参数展开; 定积分

1引言

定积分的计算是高等数学的一项很重要的基本功，文献[1-5]对常用方法和技巧作了归纳和总结.这些方法，对常见的定积分计算有很大帮助，但对一些不常见的定积分的计算，作用不大.此时，必须借助傅里叶级数法[6]，参数展开法和围道积分法[7,8]来计算.文献[6]方法关键之处在于找到一些(特殊)函数的傅里叶级数法展开式，而文献[7，8]在于得到一些含参数积分的解析表达式.本文继续推广文献[6-8]的方法，得到了一些数学手册上还未收录的积分公式.在下文的计算过程中，积分和求和顺序，积分和参数运算(求和,展开,积分)经常互换，其合理性由结果的正确性验证，不再一一细述.

2傅里叶级数法

先简要推导几个函数的傅里叶级数展开式.由以下级数展开:

(1)

在(1)式中令z=rexp(iθ), 0

(2)

对比(2)式的虚部，得到

(3)

(3)式两边乘以ln2r，在区间(0,1)内积分，得到

(4)

由积分公式

(5)

(4)式化为

(6)

(6)式右边的傅里叶级数有解析表达式[9,10]

(7)

由此得到(4)式的最终结果

(8)

有以下级数展开:

(9)

(10)

在(9-10)两式中把z延拓到z=exp(iθ)，由以下式子

(11)

(12)

对比(9-10)式两边实部，得到

(13)

(14)

(13)式两边除以θ2+α2，在区间(0,∞)内积分，并利用积分公式

(15)

计算得到

(16)

利用无穷求和式

(17)

计算得到

(18)

同样(14)式两边除以θ2+α2，在区间(0,∞)内积分，并利用积分公式(15)式，计算得到

(19)

有以下级数展开:

(20)

在(20)式中令z=rexp(iθ),0

(21)

对比(20-21)式的实部和虚部，得到

(22)

(23)

(23)式中作代换θ→π/2-θ，得到

(24)

(22)式两边除以sinθ，在区间(0,π/2)内积分，得到

(25)

利用积分公式

(26)

计算得到

(27)

(24)式两边除以sinθ，在区间(0,π/2)内积分，计算得到

(28)

利用积分公式(26)式，计算得到

(29)

3参数求和法

由文献[9，10]，Zeta函数ζ(s,a)定义为

(30)

且有以下的积分表示

(31)

(31)式两边对参数a求和，并利用以下公式

(32)

计算得到以下积分表达式

(33)

(33)式中的无穷求和为

(34)

由Zeta函数ζ(s,a)的定义式(30)式

(35)

(35)式中的两重无穷求和可以重新拆分为

(36)

继续拆分求和，计算得到

(37)

由此得到(33)式的另外表示

(38)

由(31)式和(32)式，得到以下积分表示

(39)

即

(40)

由Zeta函数ζ(s,a)的展开式[9,10]

(41)

(42)

以及

(43)

当s→0，计算得到以下积分表示式

(44)

其中ψ(a)=Γ′(a)/Γ(a)是伽玛函数的对数微商.

4参数展开法

定义一个含参数a的函数为

(45)

由正切函数的指数函数展开

(46)

再作变量代换z=exp(2iθ)，得到

(47)

积分路径是从上半单位圆周上顺时针方向.把路径改为从实轴的-1到+1，因为闭合路径内没有极点，积分化为

(48)

先计算以下积分

(49)

(50)

其中B(α,β)是贝塔函数.另一个积分是

(51)

(52)

(48)式的积分分为两区间(-1,0)和(0,1)积分之和

(53)

代入(50)和(52)式，计算得到

(54)

I(a)有两个表达式，一个是积分表示(45)式，一个是特殊函数表示(54)式，把它们在a=a0处展开，得到

(55)

取a0=1，对比展开式(55)式的第三项(可以借助数学软件解析计算)，得到以下积分公式：

(56)

对比展开式(55)式的其他阶展开系数，可以得到一系列的积分公式，篇幅所致，不再详述.

5结论

以上定积分的解析式，都得到数学软件数值计算结果的检验，说明本文所用的方法是合理正确的.

[参考文献]

[1]宁荣健.定积分计算的方法和技巧[J].工科数学,1995,1(11)：199-203.

[2]张俊祖.定积分的一些计算方法和技巧[J].高等数学研究,1996,4：27-28.

[3]李开丁,李莉.定积分的两种换元法及其应用[J].高等数学研究,1999,2(4)：15-18.

[4]王贵君.递推序列在一些定积分计算中的巧妙应用[J].高等数学研究,2000,3(4)：29-32.

[5]钱林,杨巧林.妙用公式求积分[J].高等数学研究,2004,7(6)：45-47.

[6]郑晨,邱为钢.基于傅里叶级数的定积分计算技巧[J].高等数学研究，2010,,13(3)：31-32.

[7]邱为钢,唐荣荣.对数三角函数的定积分[J].大学数学，2011,27(5)：134-137.

[8]邱为钢,倪仁兴.用参数展开法计算一类含对数函数的定积分[J].大学数学,2011,27(6)：174-176.

[9]王竹溪,郭顿仁.特殊函数概论[M].北京：北京大学出版社，2000.

[10]Gradshteyn I S., Ryzhik I M. 积分，级数和乘积表 [M].7版.北京:世界图书出版公司,2007.

Evaluation of Some Definite Integrals

QIUWei-gang

(School of Science, Huzhou Teacher’s College, Huzhou, Zhejiang 313000, China)

Abstract:Some definite integrals are obtained by the Fourier series method, parameter summation method and the parameter expansion method.

Key words:Fourier series; parameter expansion; definite integrals

[基金项目]国家自然科学基金(11275067,11475062)； 浙江省高等学校创新团队(T200924)

[收稿日期]2014-08-09;[修改日期]2015-01-08

[中图分类号]O172.2

[文献标识码]C

[文章编号]1672-1454(2015)01-0062-05