浅议函数与方程思想的运用

☉江苏省仪征技师学院教务处 徐海波

浅议函数与方程思想的运用

☉江苏省仪征技师学院教务处 徐海波

函数与方程思想是中学数学的重要思想方法之一，其首次出现在高中数学新知学习不久.这是一种知识性的思想方法，将函数与方程之间建立了桥梁、进行了沟通.函数与方程思想最初出现应该是在初高中衔接的一元二次不等式的解法这一内容中，从这里学生清晰地理解了一元二次函数、一元二次方程，以及一元二次不等式之间的紧密联系（如下表），函数与方程之间的相互转化已经在头脑中初具雏形.

判别式Δ=b2-4acΔ＞0Δ=0Δ＜0二次函数y= ax2+bx+c（a＞0）的图像一元二次方程ax2+bx+c=0（a＞0）的根y y x1 y O x2 x O x1=x2x O x有两相异实根x1，x2（x1＜x2）有两相等实根x1=x2=-b 2a没有实数根ax2+bx+c＞0（a＞0）的解集｛x|x＜x1或x＞x2｝｛x|x≠x1｝｛x|x∈R｝ax2+bx+c＜0（a＞0）的解集｛x|x1＜x＜x2｝ØØ零点个数两个一个无

随着基本初等函数学习的深入，我们也发现了更多的方程问题可以转化为函数求解，也可以将其转换为不同函数之间的交点问题，这正是提高了将陌生问题转换为熟悉问题解决的能力.

一、方程问题函数化

中学数学中的方程主要是一次方程、二次方程，以及少数分式方程、高次方程、无理方程等.有些与方程相关的问题并不宜直接求解，原因是方程内部的变化太巧妙.如：二次方程，用代数的方式比较容易解决两正根问题，只需要韦达定理和判别式，但是同样的方式却不太容易解决两根均大于1，很明显会将解的范围进行扩大，因此利用函数图形的运动变化，可以较为自然地将其内部变化分析清楚.

例1已知关于x的二次方程x2+2mx+2m+1=0.

（1）若方程有两根，其中一根在区间（-1，0）内，另一根在区间（1，2）内，求m的范围；

（2）若方程两根均在区间（0，1）内，求m的范围.

分析：由二次方程y=ax2+bx+c（a＞0）的图像观察，a为1，有2个实根就是Δ＞0的情形，再可画出相应的示意图如图1所示，再根据2个根所在的区间求解.

解：（1）由条件，抛物线f（x）=x2+2mx+2m+1，与x轴的交点分别在区间（-1，0）和（1，2）内，如图1所示，得

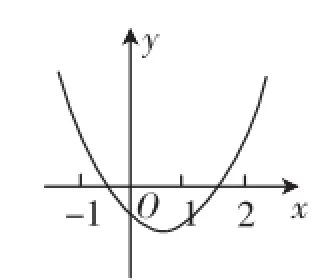
图1

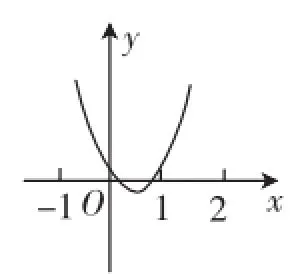
图2

说明：对二次函数的零点问题，可以采用根与系数的关系和判别式解决；比较复杂的题目，可利用二次函数的性质结合图像寻求条件.二次函数与方程之间的转换研究，主要依赖二次函数的开口、对称轴、端点处的函数值等一系列约束条件，从而轻松地避开了求根公式的运用.这一类问题较为常见，是初学者需要掌握的.

例2若方程22x+2xa+a+1=0在实数范围内有解，求实数a的取值范围.

分析：笔者将问题给学生观察，学生的第一反应是对其进行换元，将其转化为二次方程.考虑到换元之后变量的取值范围，进一步转化为相对应的二次函数问题求解；有少数能力较高的学生，可以通过参变分离的方式看透问题更简洁的本质，其本质是在自变量变化情形下，求函数值域的问题.

解法1：设t=2x（t＞0），则原方程可变为t2+at+a+1=0（*），原方程有实根，即方程（*）有正根.令f（t）=t2+at+a+1.得-1＜a≤2-2√2；②若方程（*）有一个正实根和一个负实根（负实根，不合题意，舍去），则（f0）=a+1＜0，解得a＜-1；③当a=-1时，t=1，x=0符合题意.综上，a的取值范围

说明：本题的解法1较为常规地将问题转化为函数零点处理，考虑到对称轴并非确定，因此必须对函数的对称轴进行分类讨论，此法的优点是对思维的要求并不高，但是必须介入分类讨论思想；解法2将问题上升到一个全新的高度，对于“a=f（x）有解”型问题，可以通过求函数y=f（x）的值域来解决.

二、函数问题的转化

如果说方程问题可以转化为函数的话，那么函数问题如何借助方程进行处理呢？有些函数直接处理是较为烦琐的，我们可以借助方程将其进一步转换为熟悉的函数问题进行解决.

（1）若y=g（x）-m有零点，求m的取值范围；

（2）确定m的取值范围，使得g（x）-（fx）=0有两个相异实根.

解析：（1）若函数y=g（x）-m有零点，那说明函数y= g（x）跟函数y=m有交点，函数g（x）=（x＞0）的大致图

像如图3所示，由图可知y=g（x）是不变的函数，所以只要函数y=m在2e上面即可，所以m≥2e.

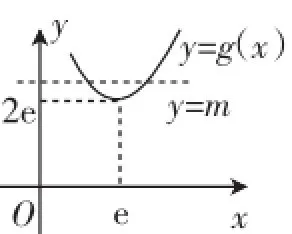
图3

图4

（2）由（1）可知要使g（x）-f（x）=0有两个相异实根，则y=f（x）与y=g（x）的图像有两个不同交点.因为f（x）=-x2+ 2ex+m-1=-（x-e）2+m-1+e2，所以其图像的对称轴为x=e，开口向下，最大值为m-1+e2.画出两个函数的大致图像，如图4所示，故当m-1+e2＞2e，即m＞-e2+2e+1时，函数g（x）与f（x）有两个交点，所以m的取值范围是（-e2+2e+1，+∞）.

说明：我们较为巧妙地将方程转化为两个不同函数的交点问题来解决，这种将单一函数拆变为两个函数的解决方式，一直是处理稍难函数的常规手段.随着问题解决方法的多样性学习，后续还有更巧妙的知识工具使用，诸如运用导数来解决函数零点问题、方程根问题，限于篇幅不展开赘述.

总之，函数与方程是紧密联系的两个知识，函数与x轴相交的交点恰为其方程的根，因此可以将方程看成是函数值为0的特殊情形，研究函数零点也就变成了研究方程的问题；反之，方程是函数的特殊位置，解决方程问题可以利用图像的特征和变化，因为直观化的图形思维才是问题解决最容易接受和最容易分析的.因此总体而言，函数与方程的思想在解决零点、根等问题时，我们尽可能将其转换为函数问题，利用函数图形或分解为多个函数进行求解，这正是高中数学以函数章节为核心的重要体现，也是教师教学这一内容需要积极关注和渗透的.限于篇幅，笔者未就零点相关的其余问题展开叙述，请读者对本文拙见给出补充.

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2002.

2.李大.运用整体思想求数列［J］.中学数学（上），2012（10）.F