融入数学文化演绎精彩课堂
☉江苏省海州高级中学 徐进勇
融入数学文化演绎精彩课堂
☉江苏省海州高级中学 徐进勇
数学文化从狭义上讲是指数学的思想、精神、方法、观点、语言,以及它们的形成和发展;广义上除了上述内涵以外,还包含数学家、数学史、数学美、数学教育,以及数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等.[1]
数学文化是新课程的基本理念,数学文化被看作是理解数学的一种途径.《普通高中数学课程标准(实验)》把数学文化作为教学内容并提出教学要求,明确指出:“数学是人类文化的重要组成部分.数学课程应适当介绍数学的历史、应用和发展趋势,数学对推动社会发展的作用,数学的社会需求,社会发展对数学发展的推动作用,数学科学的思想体系,数学的美学价值,数学家的创新精神.数学课程应帮助学生了解数学在人类文明发展中的作用,逐步形成正确的数学观.”数学课程改革的一个重要的标志就是数学文化走进了数学课程标准和中小学数学教科书.数学文化具有极强的内在逻辑性、历史发展的延续性和广泛的外部联系,教师可以挖掘数学课程中许多模块的独特文化背景,利用问题、方法的背景或者产生的曲折历程,融入课堂教学之中,发挥激情、引趣、启真、促思功能,使课堂教学更具探究性、趣味性、应用性.下面谈谈数学文化在教学中的应用.
一、追求知识本源
数学知识的产生与发展必有其前因后果.作为数学教师不仅要透彻地了解他们所教的那一部分数学,而且还应从宏观上来认识数学知识的发生与发展,从而能够知其然也知其所以然,才能教其所以然.教师在引导学生学习一些常见的数学概念、公式和方法时,如果能够指出它们的来源、典故及历史演变过程,并以此创设恰当的情境引入新课,把看似简单的教材还原成丰富多彩的教学内容,让学生感受数学思想方法中闪烁的智慧,欣赏到数学的外在形式与内在的美,在迫切的愿望下参与教学,这些都是高质量的文化传承,也是无痕的育人.例如,当我们讲到解析几何这一章时,可以先讲解析几何的产生和发展的过程,当然也要介绍解析几何的创始人笛卡儿,讲述笛卡儿发明坐标系的过程.在讲复数时我们可以从1545年意大利数学家卡尔丹提出的问题“把10分成两部分,使其乘积为40”出发,引出数系的发展过程,再讲到大数学家柯西.在讲授“古典概率”时,可以借助数学史引入主题:十七世纪,法国贵族德·梅耳非常喜欢抛掷骰子赌点数大小来赌博,在经常抛掷的过程中,发现了一个令他困惑的问题:他把一个骰子连续抛了四次,发现至少出现点是六的时候多一些;可是他同时将两个骰子连续抛了24次,发现至少出现点数是双六点的时候要少一些.这是怎么一回事呢?这就是概率论历史上著名的德·梅耳问题.但他自己无法给出答案,于是就写信给当时的法国数学家Pascal(帕斯卡),Pascal和当时的一流数学家Fermat(费尔马)一起通信讨论.后来荷兰科学家Higgins(惠更斯)来到巴黎听说这个问题,觉得这个问题也有意思,对此进行了研究.1657年,他写了自己研究问题的专著《论赌博中的计算》.应该说帕斯卡、费尔马、惠更斯是早期概率论的创始人.至此提出问题:你能帮德·梅耳解决他的困惑吗?这样引入,不仅使学生增长见识与提高兴趣,更有利于学生对新知识的接纳与理解,学生学的高兴、学的自然.
二、启迪数学思考
文化是具有传承性的,数学文化也不例外.高中数学内容中的数与形、曲与直、常量与变量、连续与间断、有限与无限、抽象与具体、偶然与必然等内容都体现了辩证法中的同中有异、异中有同、相互转化的思想,凝聚着数学前辈们对数学本质的认识和数学地解决问题的策略,值得我们学习、借鉴.
案例1苏教版必修5“等差数列的前n项和”,课本是这样引入的:某仓库堆放一堆钢管,如图1,最上面的一层有4根钢管,下面的每一层都比上一层多一根,最下面的一层有9根,怎样计算这堆钢管的总数呢?假设在这堆钢管旁边倒放着同样的一堆钢管,如图2,这样,每层的钢管数都等于4+9,共有6层,从而原来一堆钢管的总.然后再提出:如何求等差数列{an}的前n项和Sn?
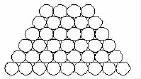
图1

图2
看起来极为普通和常见的计算钢管总根数的问题,通过一幅图向我们展示了等差数列求和的具体方法——倒序相加法.这种直观演示形象、具体、自然,学生容易接受,学生不仅掌握了数学知识,体会到数学方法,更是领悟到数学的妙趣.数学家华罗庚对“数形结合”思想方法进行这样的精辟总结:“数形本是相倚依,怎能分作两边飞;数缺形时少直觉,形少数时难入微;数形结合百般好,隔离分家万事休;几何代数统一体,永远联系莫分离.”至此,教师也可以插入数学小故事:德国的“数学王子”高斯如何计算:1+2+3+…+100.通过这样的启发引导,此时学生学习思路被打开,学习兴趣被激发,学习热情被点燃,学生在体验中学习和感悟到数学思想方法,在愉悦中放飞思维,而这种思想方法的掌握还有利于研究下一章等比数列的求和.
三、突破思维瓶颈
数学在其长期的发展过程中,形成了许多数学观点中的数学文化.如“对称”观点、“类比”观点、“数理统计”观点、“数学机械化”观点、“相容性、独立性和完全性”观点等,它们对数学地解决疑难问题提出了新思路、新视角、新观点.
案例2在立体几何学习中,学生提出问题:4个平面最多把空间分为几个部分?
这是数学观点中典型的“分割问题中的类比”问题.为此,教师“顺带”学习苏教版必修2立体几何章节后阅读材料“平面几何与立体几何的类比”,内容如下:类比是根据两个对象在某些方面的相同或相似,推出它们在其他方面的相同或相似点的一种推理方法.平面几何和立体几何在研究对象和方法、构成图形的基本元素等方面是相同或相似的,因此,在两者之间进行类比是研究它们性质的一种非常有效的方法.为解决学生提出的问题,我们想到了空间四面体,如图3,把四面体的四个面延展成四个平面,就能把空间分为最多的部分了.那么现在把空间分成几个部分呢?暂难想象.由此我们想到类比“直线分割平面”的情形.引导学生思考:3条直线最多把平面分为几个部分?这可以把三角形的三条边延长为直线,得3条直线最多把平面分为7个部分,这7个部分的特点:一个是有限的部分,在三角形内部,即①;其余6个是无限的部分,其中②,③,④与三角形有公共顶点,⑤,⑥,⑦与三角形有公共边,如图4.

图3
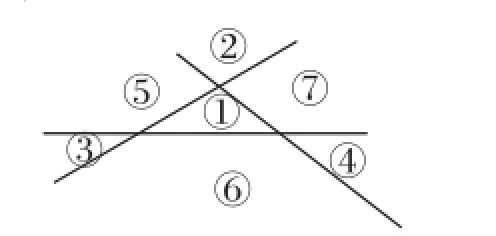
图4
在上面推理的基础上,类比考虑四面体的4个面延展成4个平面,把空间分为几个部分:有限部分(四面体内部)数为1;无限部分与原四面体或有一个公共顶点(有4个部分),或有一条公共棱(有6个部分),或有一个公共面(有4个部分),于是所分空间总的部分数为15.当然,这是一种合情推理,还需要用演绎推理分析证明这一猜测,分析方法仍需要类比直线分平面、点分直线,从而寻找到它们间的一种数量关系,得n个平面最多把空间分为(n3+5n+6)个部分.可见,“类比”是获得新思路、新发现的一种观点、一种手段.掌握“类比”的观点,学会“类比推理”的方法,是提高学生创新能力的一种有效途径.
四、拓展探究空间
知识是不能现成地传递的,而要回到它的经验状态,通过学生的亲身体验实现转化.这样,学生理解得会更透彻,掌握得更灵活,同时也能引起学生兴趣,产生学习的内驱力.
案例3苏教版必修1“对数”一节中,对概念的学习,教师大都通过指数,如指数函数解决了2b=?的问题,反之,如果知道2b=8,2b=9,如何求b?一般地ab=N,如何求b?从而引出对数的概念.
事实上,历史中对数的发明背景是为简化计算而产生的,实质是化乘除为加减,化乘方、开方为乘除运算,为此,若将这段数学史融入教学可作如下设计:
问题1:计算:(1)32×256=?(2)4096÷128=?
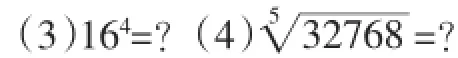
教师介绍:16世纪前期,欧洲人热衷于地理探险和海洋贸易.特别是地理探险需要更为准确的天文知识,对计算速度和准确度的要求与日俱增,人们希望将乘除法归结为简单的加减法.
问题2:尝试改写,使运算简化.

问题3:如何计算36×365=?
学生:如果能知道2的多少次方等于36和365,就可算出结果.
老师:是的,实际上在17世纪人们就制作了这样包含足够多数字的表格,通过查表的方式解决上述问题,这期间有许多人为了制作这样的一张精确的表格而献出了自己毕生的精力,从而达到将计算化繁为简的目的.当然36也可以用其他数作底来表示,如36=10x,36=ax等.为了表达x,苏格兰数学家纳皮尔(1550~1671年)发明了对数,并于1614年在《论述对数的奇迹》中,介绍了他的方法和研究成果.在纳皮尔著作发表40年后,对数传入我国,并逐步演变成对数,意指“对照表中的数”.然后教师再给出对数的具体概念.[2]
这样的引入给学生展示了一个波澜壮阔的大时代,使学生逐步认识对数发明的意义和对数的发展历史.还原了知识形成的过程,创设了数学问题的探究空间.可见,将数学文化融入课堂,可以将新课程“知识与技能、过程与方法、情感态度与价值观”这三维目标互相影响、互相作用、有机整合,从而有效地培养学生的数学科学文化素养,发展学生的实践能力和创新精神.
五、增强实际应用
弗赖登塔尔则强调:“要保证有活力(是指数学知识的活力),就必须教给学生充满着联系的数学.”数学源于生活,又高于生活,数学文化的意义不仅在于知识本身和它的内涵,更由于它广泛的应用价值.如近年来,国家对食品、礼品的包装提出“摒弃奢华包装,力求朴素节俭”.笔者以此为背景,在导数的应用中安排了一节数学应用课.
案例4实际包装中的数学.
问题1:如图5,有一个各条棱长均为a的正四棱锥,现用一张正方形包装纸将其完全包住,不能剪裁,但可以折叠,则包装纸的最小边长是多少?

图5
问题2:某商场为促销要准备一些正三棱锥形状的装饰品,用半径为10cm的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图6所示.设正三棱锥的底面边长为xcm,体积为Vcm3.在所有能用这种包装纸包装的正三棱锥装饰品中,V的最大值是多少?并求此时x的值.

图6
体验2011年江苏数学高考题第17题:请你设计一个包装盒,如图7所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.

图7
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
从教学的效果来看,学生不仅获得了用数学知识解决实际问题的方法与喜悦,还感受到数学图形的对称美、数学方法的统一美,增强了学生的“节约”意识.事实上我们常见的市场销售问题、用水用电问题、运输问题、税收问题、医疗费用问题、银行储蓄问题等,都是以生活实际为背景的,这些教学的具体素材,可以使学生进一步了解数学科学与人类社会发展之间的相互关系,体现数学工具性、价值性、科学性和人文性,使数学教学血肉丰满,真正做到教书育人.
六、激发学习热情
数学教育如果过于注重数学的形式化、逻辑性,会让学生感到数学是“冰冷的美丽”,从而忽视数学教育在培养学生人文素养方面的作用,把数学中的“火热的思考”、重要的人文价值泯灭在其中.数学课堂教学中如能恰如其分地引用数学故事定能突破数学课堂的单调,营造出富有文化气息的课堂氛围,达到以知促情、知情结合的目的.如通过介绍数学家获得真理的艰苦过程,使同学们知道每一个定理背后的艰辛.这些对于同学们自己去克服困难,发现问题是非常有利的.我国数学家华罗庚十九岁那年,因病左腿残疾,走路要左腿先画一个大圆圈,右腿才能再迈上一小步,对于这种奇特而费力的步履,他曾幽默地戏称为“圆与切线的运动”,逆境中他顽强地与命运抗争,誓言是:“我要用健全的头脑,代替不健全的双腿!”他把自己的毕生精力,投入到发展祖国的科学事业特别是数学研究事业之中.他一生为我们留下了200余篇学术论文,10部专著,其中8部为国外翻译出版,有些已列入本世纪数学经典著作之列.他的名字已载入国际著名科学家的史册.数学家陈景润身居陋室,但为了攻破歌德巴赫猜想这一世界数学难题,不断演算,通过努力终于摘取了数学皇冠上的明珠,他们是中国科学界的骄傲,是中华民族的骄傲!我们在高中数学教学中恰当引入数学家的故事并不期望每一位学生都成为数学家,但数学家的奋斗经历与对数学的痴爱之情将培养学生对数学的兴趣,激发学习数学的动机.
七、领会美学价值
数学是美的.数学概念的简洁性、严格性,结构系统的协调性、统一性,数学命题和数学模型的概括性、典型性和普遍性,数学中的奇异性等,把自然规律抽象成一幅幅现实世界与理想世界的完美图像,构成了美丽动人的数学世界.
案例5苏教版必修2“圆的方程”课后练习中有这样一道题:已知点M(x,y)与两个定点O(0,0),A(3,0)的距离之比为,那么点M的坐标应满足什么关系?画出满足条件的点M所构成的曲线.我们知道点M所构成的曲线就是阿波罗尼奥斯圆.江苏高考数学卷2005年、2008年、2013年均以此为材料出题,体现数学文化在高考试题中的融入,引起了广大教育工作者的关注.笔者以此为契机,作以下介绍:已知平面上两点A、B,则所有满足=k(k≠1)的点P的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼奥斯发现,又称阿氏圆.后人把阿波罗尼奥斯(公元前262~前190)、欧几里得、阿基米德合称为亚历山大前期三大数学家.阿波罗尼奥斯对圆锥曲线的研究十分系统、完美,写成了《圆锥曲线论》八卷,将圆锥曲线的性质网罗殆尽.他将椭圆、双曲线、抛物线统一定义为:平面上到一定点的距离与到不过该定点的定直线的距离之比为常数e的动点的轨迹;从空间曲线的角度去观察它们,发现可以统一地用平面去截对顶圆锥而得到;在极坐标下它们的标准方程可以统一为:在直角坐标系下,方程可以统一为:(1-e2)x2+y2-2e2px-e2p2=0.17世纪的开普勒和18世纪的欧拉用运动、变化观点,把各种圆锥曲线看作在同一个系统中的看法:圆、椭圆、抛物线、双曲线和由两相交直线构成的退化圆锥曲线,都可以从其中一个连续地变为另一个,只需要考虑焦点的各种移动方式(多媒体展示).科学家的研究让我们看到:只有抓住了不同事物的共同本质,才能用统一的观点、统一的语言来描述不同的事物.事物的本质是内在的,当我们用统一的语言把它叙述出来时,这种内在的本质就外显化了,让我们有一种“透过现象看本质”的快感,使我们体会到数学的“统一美”.
日本数学教育家米山国藏说过:“学生在初中、高中等接受的数学知识,因毕业进入社会后几乎没有什么机会应用这种作为知识的数学,所以通常是出校门后不到一两年,很快就忘掉了.然而,不管他们从事什么业务工作,唯有深深地铭刻于头脑中的数学的精神、数学的思维方法、研究方法、推理方法和着眼点等(若培养了这方面的素质的话),却随时随地发生着作用,使他们终身受益.”课堂教学将数学知识学习与数学文化的有机结合,不仅使学生学习知识,形成技能,发展思维,还能感受数学思想,体悟理性精神,感受数学之美.让学生觉得数学课有意思、有智慧,达到立德树人之效.与数学文化相关的教学实践和研究值得重视.
1.顾沛.数学文化[M].北京:高等教育出版社,2008.
2.王华民,侯斌.从一堂概念课的不同导入谈数学史融入教学[J].数学通报,2014(8).

