注重基础创新达到平稳过渡——2015年安徽省高考数学试卷评析

☉安徽省合肥第八中学 孙勇军☉安徽省合肥市教研室 许晓天

注重基础创新达到平稳过渡
——2015年安徽省高考数学试卷评析

☉安徽省合肥第八中学 孙勇军☉安徽省合肥市教研室 许晓天

安徽省数学高考自主命题始于2006年，时至2015年已经走过了十年的历程.今年的安徽省数学高考试题是安徽省自主命题的收关之作，明年将使用全国课标卷.仔细研读试题，颇感命题专家的意图与苦心，降低难度，凸显“过渡”.

一、总体分析

1.考点常规——题型与分值稳定今年的安徽高考数学试卷与往年的安徽高考数学试卷结构和分值相同：单项选择题10道，填空题5道，每题5分，共75分；解答题6道，共75分.数学试题考查的内容常规，重点内容常考不殆.以下是今年高考数学试卷知识点分布及分值分布统计表.

2015年安徽高考数学试卷知识点分布及分值分布统计表

2.难度降低——平稳与过渡凸显

今年的理科数学试题难度明显降低，首先，前8个选择题均是较基础的题目，不需要太多的计算便可作答.降低选择题难度后使考生心理放松，能充分发挥其水平.其次，填空题的难度也有所降低，第16题往往是安徽省命题者“匠心独运”的问题，是具有较高选拔性的问题之一，但今年试题的难度有较大的降低.最后，6个解答题由浅入深，由易到难，几乎每题都易于入手，避免了过去特难的题目（如2010年理科21题，2013年理科21题，2014年理科21题，得分率极低，无法反映考生的真实水平，失去选拔功能）.

数学试题难度的降低，有利于减轻中学生的学习负担.克服了过去高考数学成绩分布长期集中于低分段的状况，提高了数学学科在高考评价中的地位.更重要的是，全国课标卷的相对难度往往是低于以往安徽省自主命题难度的，今年的试题为明年教师的高考复习教学提供了难度上的参考，为平稳衔接到明年的新课标卷的高考，做了有益的铺垫.

3.考查知识——基础与重点并重

文、理科试题对知识的考查，都特别注重考查高中数学的基础知识，但并不刻意追求知识的覆盖面，着重考查了支撑学科知识体系的主干知识，以重点知识为主线组织全卷的内容.如函数与导数，文、理科分别占33分和21分，三角函数、解三角形等每年都作为重点考查内容.理科前8道选择题都是考查基本概念和公式的题型，都可以在课本习题中寻找到其“母题”或其“影子题”.

4.文、理试卷——差距进一步缩小

以往安徽省高考文理科数学试题差异较大，去年文理科试卷内容重叠的考题有8道，其中3道完全相同的试题，5道部分一致的姊妹题.

今年文、理科数学试卷15个选择题、填空题中，相同的有6个，共30分；6个解答题中有一道解析几何题基本相同，全卷文、理科相同试题的分值为46分.可见差距进一步缩小.

要引起我们注意的是，今年文科第16题三角函数题难度比理科第16题解三角形要难一点，所以今年安徽省文科平均分与理科平均分的差距也进一步加大.这也许是命题专家从更长远的文理合卷的角度思考的结果.从文、理科相同试题得分情况看，今年文科考生数学水平较理科考生差异较大，如：基本相同的解析几何题，理科平均4.8分，文科仅为2.99分.这一现象应该引起中学数学教育，特别是今后安徽省数学高考复习的注意.

二、具体特色

1.题型常规方法多

如今年的立体几何题，结论是证明线线平行与求二面角的余弦值.载体是正方体截去一个角得到的多面体.题型常规，情景熟悉.本题对空间想象能力的考查与计算紧密结合，而且有多种途径可以解决问题，给考生以发挥的空间.

第19题（本小题满分13分）如图1所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于点F.

图1

（Ⅰ）证明：EF∥B1C；

（Ⅱ）求二面角E-A1D-B1的余弦值.

方法1：（Ⅰ）由正方形的性质可知A1B1∥AB∥DC，且A1B1=AB=DC，所以四边形A1B1CD为平行四边形，从而B1C∥A1D.又A1D⊂面A1DE，B1C⊄面A1DE，于是B1C∥面A1DE.又B1C⊂面B1CD1，面A1DE∩面B1CD1=EF，所以EF∥B1C.

（Ⅱ）因为四边形AA1B1B，ADD1A1，ABCD均为正方形，所以AA1⊥AB，AA1⊥AD，AB⊥AD.

图2

而E为B1D1的中点，所以E点的坐标为（0.5，0.5，1）.

设面A1DE的法向量n1=（r1，s1，t1），而该平面上向量得r1，s1，t1应满足的方程一组解，所以可取n1=（-1，1，1）.

设面A1B1CD的法向量n2=（r2，s2，t2），而该平面上向量由此同理可得n2=（0，1，1）.

所以结合图形知，二面角E-A1D-B1的余弦值为

方法2：（Ⅰ）在平面B1A1D1内作连接C1D1，C1C，C1F，C1E，如图3所示，所以四边形A1B1C1D1为平行四边形，从而

又因为四边形AA1B1B，ABCD均为正方形，所以于是，故四边形CDD1C1为平行四边形.

在平行四边形A1B1C1D1中，E为B1D1的中点，所以A1，E，C1三点共线，从而面A1ED与面A1C1D为同一平面.故F为CD1与C1D的交点，即F为CD1的中点.所以EF∥B1C.

（Ⅱ）连接C1B，交B1C为M点，取A1D中点N，连接C1N，MN，如图4.

因为CC1∥DD1∥AA1，而AA1⊥AB，AA1⊥AD，且AB∩AD=A，所以AA1⊥面ABCD，从而CC1⊥面ABCD.

所以ABCD-A1B1C1D1为正方体，因而C1M⊥B1C.

又A1B1⊥面B1C1CB，所以C1M⊥A1B1.又A1B1∩B1C= B1，所以C1M⊥面A1B1CD，从而C1M⊥A1D.

在三角形A1C1D中，A1C1=C1D，N为A1D的中点，从而C1N⊥A1D.

因为A1B1⊥面A1D1DA，从而A1B1⊥A1D，而MN∥A1B1，所以MN⊥A1D，从而∠C1NM为二面角E-A1D-B1的平面角.

设正方体的边长为1，在Rt△C1MN中，MN=1，C1M=

图3

图4

所以二面角E-A1D-B1的余弦值

图5

又平面A1ED∩CD1=F，F∈CD1，所以M点与F点重合，即EF∥B1C.

（Ⅱ）连接AD1，交A1D于点Q，连接B1Q，取B1Q中点P，连接EP，如图6.

过点P作PO∥A1B1交A1Q于点O，连接EO.

因为AB⊥AD，AB⊥AA1，AD∩AA1=A，所以AB⊥面ADD1A1.从而AB⊥D1Q，A1B1⊥D1Q.

又因为D1Q⊥A1D，D1Q⊥A1B1，A1D∩A1B1=A1，所以D1Q⊥面A1B1CD.

又因为EP是△B1QD1的中位线，所以EP∥D1Q，所以EP⊥面A1B1CD.

又因为A1B1⊥A1D，所以PO⊥A1D，所以∠EOP为二面角E-A1D-B的平面角.

图6

方法4：（Ⅰ）因为四边形AA1B1B，ADD1A1，ABCD均为正方形，所以AA1⊥AB，AA1⊥AD，AB⊥AD.

图7

由已知可得A1（0，0，1），B1（1，0，1），D（0，1，0），CD1的中点，所以EF∥B1C.

2.注重衔接有新意

今年高考数学试卷中的数列问题，曾经多次在高考或模考中出现过.如2009年山东理科20题考查的数列题：

等比数列｛an｝的前n项和为Sn，已知对任意的n∈N*，点（n，Sn）均在函数y=bx+r（b＞0且b≠1，b，r均为常数）的图像上.

（Ⅰ）求r的值.

（Ⅱ）当b=2时，记bn=2（log2an+1）（n∈N*）.

解析：（Ⅰ）略.

（Ⅱ）证法一：数学归纳法.

证法二：常规放缩法.

证法三：直接放缩，构造辅助对偶式.

而2015年安徽理科18题数列题注重了与上述类似考题的衔接，又推陈出新.

第18题设n∈N*，xn是曲线y=x2n+1在点（1，2）处的切线与x轴交点的横坐标.

（Ⅰ）求数列｛xn｝的通项公式；

当然也可用数学归纳法证明.

再如文科第21题，一道常规的函数与导数的压轴题，注重了试题与课本的衔接.

第21题（本小题满分13分）

仔细分析后发现此题在课本上都有原型.课本在导数应用中有这样的例题：某制造商制造并出售球形瓶装的某种饮料，瓶子的制造成本是0.8πr2分，其中r是瓶子的半径，单位是厘米.已知每出售1mL的饮料，制造商可获利0.2分，且制造商能制作的瓶子的最大半径为6cm.

（1）瓶子半径多大时，能使每瓶饮料的利润最大？（2）瓶子半径多大时，能使每瓶饮料的利润最小？

3.少算多想考思路

在以往的考试中，圆锥曲线方面题目的计算烦琐复杂，技巧性很强，对学生计算能力和细心程度都有较高要求.而今年的试题中圆锥曲线的题目不论小题还是解答题运算量都比较小，这有利于考生有一个良好的心态去解决后面的解答题，并充分发挥自己的真实水平.今年的考题更注重考查数学思维方法，选择题与填空题都不需要过多的复杂计算就可得出结论，而是重在思路的选取上.如文理20题：

第20题（本小题满分13分）

（Ⅰ）求E的离心率e.

（Ⅱ）设点C的坐标为（0，-b），点N为线段AC的中点，点N关于直线AB的对称点的纵坐标为求E的方程（理）.

（Ⅱ）设点C的坐标为（0，-b），点N为线段AC的中点，求证：MN⊥AB（文）.

方法2：设点M的坐标为（xM，yM），由题知xM＞0，yM＞0，由点M在线段AB上，题设条件知，直线OM的斜率

4.能力要求更重要

今年理科函数大题，以学生熟悉的二次函数为载体，考查了复合函数的单调性和最值.由于复合函数的单调性和最值，特别是最值平时训练少，甚至没有做过，因而得分率底.比如理科第21题，全省30万左右考生，5万2千左右考生得零分，难度系数0.18.所以加强学生创新意识的培养，提升学生的能力是当务之急.

第21题（本小题满分13分）

设函数f（x）=x2-ax+b.由此可知，z=b-满足条件D≤1的最大值为1.

方法2：D≤1即为|a|+ |b|≤1（或|a+b|≤1且|b-a|≤以看做b是a的二次函数，其图像向上平移时，z增大，最后离开区域|a|+|b|≤1接触的点为a=0，b=1.

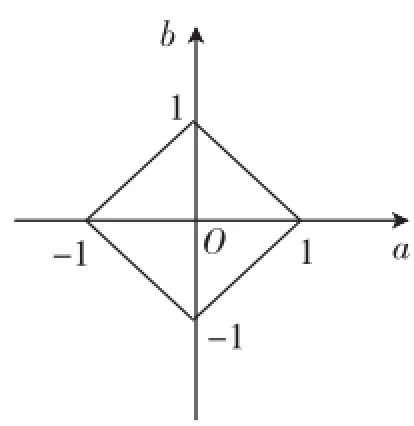
图8

从函数小题来看，如理科的第15题，文科的第10题，两个函数看似都是我们较熟悉的函数，当然如果不仔细分析两函数图像的对称性，很难解对这道题.文科的14题也是如此，研究函数图像交点个数的题型在平时练习中是常见的，但要想做对也不是很容易.

总之，安徽省今年的考题，注重了基础、衔接和创新，以期与明年安徽省开始执行的新课标数学卷有一个平稳的过渡，值得大家研究和思考.A