二次函数迭代的一个问题的探究

●陈伊遐(俄亥俄州立大学数学系俄亥俄)

二次函数迭代的一个问题的探究

●陈伊遐(俄亥俄州立大学数学系俄亥俄)

文献［1］～［3］对二次函数f(x)=x2+bx+c的迭代进行了探讨，其中文献［2］、［3］得到了关于方程f2(x)=x在特殊情形下根的一个结论:设f(x)=x2+bx+c，记Δ0=(b-1)2-4c，若方程f(x)=x有2个不等实根，则1)当0＜Δ0＜4时，f2(x)=x只有2个不等实根;2)当Δ0＞4时，f2(x)=x有4个不等实根.方程f2(x)=x中的f2(x)为f2(x)=f(f(x))，一般地有fn(x)= f(fn-1(x)).

本文将考虑一般二次函数f(x)=ax2+bx+c (其中a≠0且a，b，c∈R)的迭代，用初等方法给出了方程f2(x)=x的所有实根，显然方程f2(x)=x为x的4次方程.

记y=f(x)，即

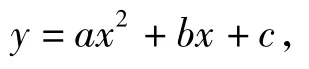
由f2(x)=x知x=f(y)，即

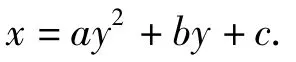
上述2式相减整理可得

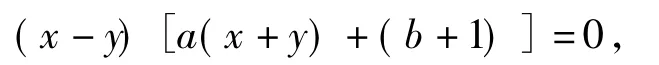
从而x-y=0或a(x+y)+(b+1)=0.

当x-y=0时，即x=ax2+bx+c，亦即

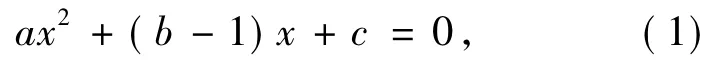
记Δ=(b-1)2-4ac，根据判别式易解方程(1).

当a(x+y)+(b+1)=0时，由方程组

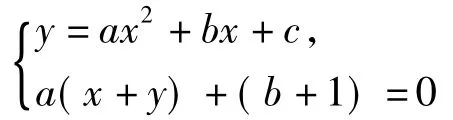
消去y，整理可得

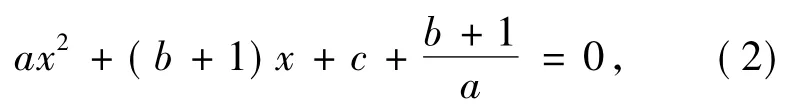
此时判别式为

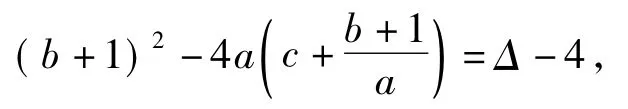
方程(2)可解，因而有:

定理1设f(x)=ax2+bx+c，记Δ=(b-1)2-4ac，则

1)当Δ＜0时，方程f2(x)=x无实根;

2)当Δ=0时，方程f2(x)=x有1个实根;

3)当0＜Δ≤4时，方程f2(x)=x有2个不等实根;

4)当Δ＞4时，方程f2(x)=x有4个不等实根.

证明当Δ＜4时，结论显然成立.

当Δ=4时，方程(1)的2个不等实根为

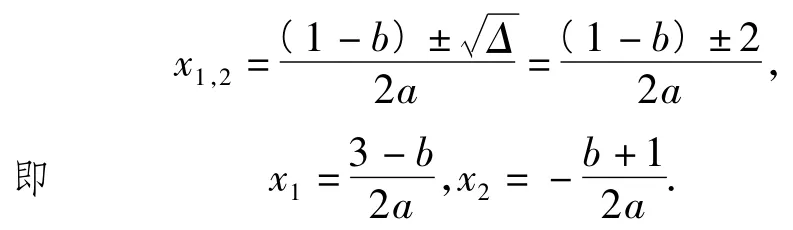
当Δ＞4时，方程(1)的2个不等实根为

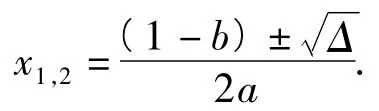
方程(2)的2个不等实根为

例1设f(x)=x2+x-2，解方程f2(x)=x.

解方程(1)为x2-2=0，解得，显然点为f(x)的不动点，此时有fn(x)=x.

方程(2)为x2+2x= 0，解得x=-2或x=0，显然点(-2，0)，(0，0)为f(x)的2-周期点，此时有f2n(x)=x.

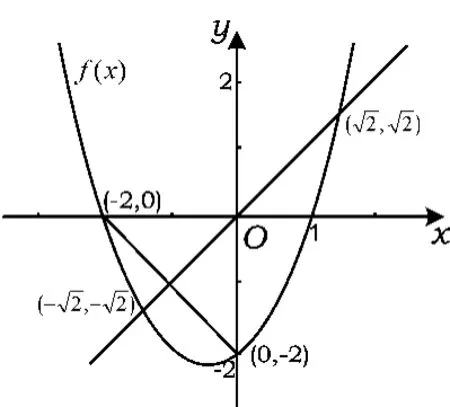
图1

因而方程f2(x)=x有4个实根:，-2，0 (如图1所示).

［1］王兴东，顾新辉.二次函数迭代的一个问题［J］.数学通讯，2005(13):24-26.

［2］陶楚国.二次函数迭代的一个问题初探［J］.数学通讯，2006(17):31-32.

［3］李永利.关于二次函数迭代的一个定理的简证［J］.数学通讯，2007(11):15.