轮换平均值不等式及其应用

●李世杰(衢州市教育局教研室浙江衢州324002)●李盛(衢州市第一中学浙江衢州324000)●汪水林(衢州市第二中学浙江衢州324000)

轮换平均值不等式及其应用

●李世杰(衢州市教育局教研室浙江衢州324002)●李盛(衢州市第一中学浙江衢州324000)●汪水林(衢州市第二中学浙江衢州324000)

本文提出了轮换平均的概念，建立了关于轮换平均的一个不等式，该不等式是算术-几何平均值不等式的一个隔离.作为其应用，得到了一系列的新不等式，最后给出轮换平均值不等式的加权推广.

1 轮换平均的定义

定义设ai＞0，pi≥0，pn+i=pi(其中i=1，2，3，…，n，n∈N，n＞1)，，我们把

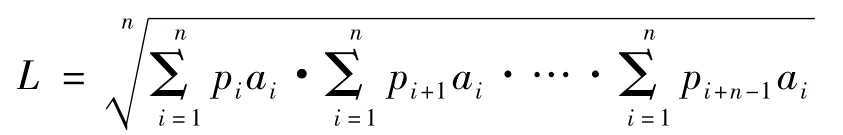
称为关于a1，a2，…，an的轮换平均.

2 主要结论

一般地，如下的轮换平均值不等式成立:

定理1设ai＞0，pi≥0，pn+i=pi(其中i=1，2，3，…，n，n∈N，n＞1)，，则有G≤L≤A，即

证明1)先证右边的不等式.利用算术－几何平均值不等式，结合，得

这就证明了式(1)右边的不等式.

2)由加权算术－几何不等式知

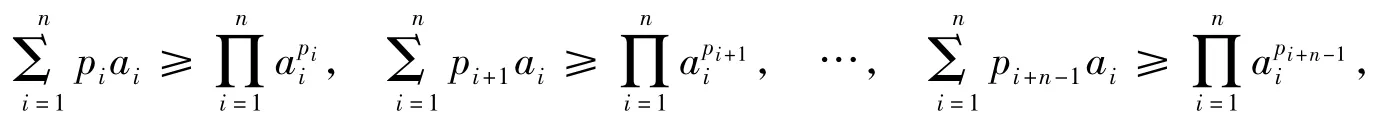
上述各式相乘得

至此知式(1)左边的不等式也成立.

定理1证毕.

注1)不等式(1)说明:轮换平均值L是n元算术－几何平均值不等式的一个隔离.

2)当n=2时，由定理1可得以下结论.

若a1＞0，a2＞0，p1≥0，p2≥0，p1+p2=1，则

3)不等式(2)具有如下的几何意义.

设A(a1)，B(a2)，AM=BQ，，则

说明对称的定比分点坐标积可以隔离算术-几何平均值不等式.

图1

4)不等式(1)等号成立的条件不唯一，当a1=a2=…=an时左、右边2个等号同时成立.

对于不等式(2)，还可以将条件a1＞0，a2＞0改进为“a1，a2是任意实数”，即为如下定理2.

定理2若p1≥0，p2≥0，p1+p2=1，则

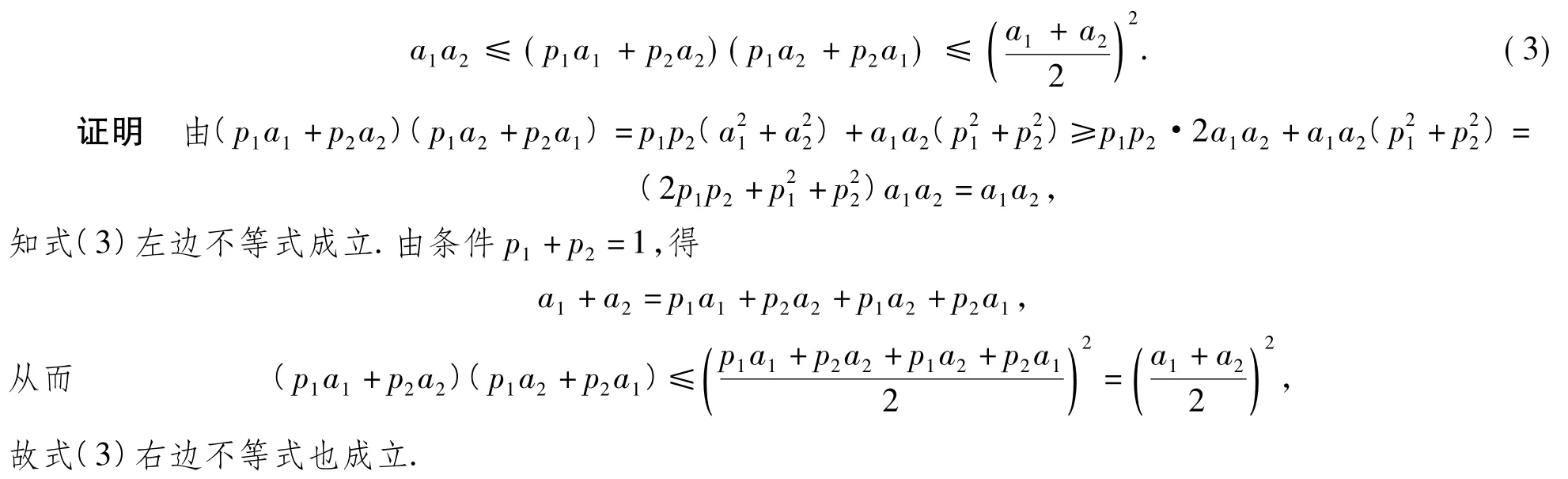
3 应用

对p1取一些特殊值，可得一系列对算术平均值与几何平均值进行隔离的新不等式.

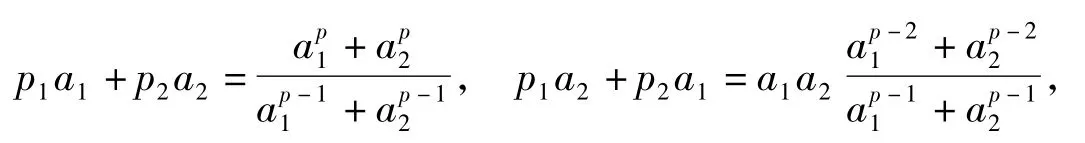
代入不等式(3)得如下结论3.

结论3若a1＞0，a2＞0，p≥1，则

4)当a1＞a2时，取，则，从而

代入不等式(3)得如下结论4.

结论4若a1＞0，a2＞0，则

5)当a1＞a2时，取，则，从而

代入不等式(3)得如下结论5.

结论5若a1＞0，a2＞0，则

6)当a2＞a1时，取，则，从而

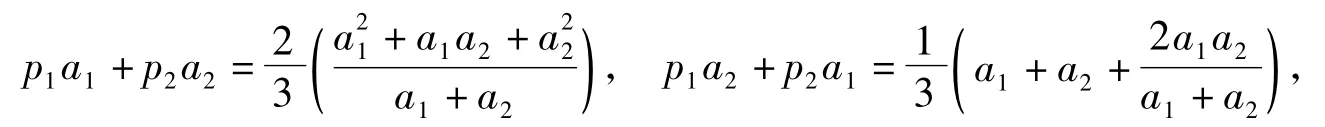
代入不等式(3)得如下结论6.

结论6若a1＞0，a2＞0，则

注因为结论4～6中的不等式关于a1，a2是对称的，所以条件a1＞a2或a2＞a1可省略.

从上可见，从定理1的一个特例:一个加权的简单不等式(2)出发，通过选取不同的p1，p2值，就可以得到许多新的不等式.同样地，对于二元以上的轮换平均值不等式，通过选取不同的pi值，也可以得到许多新的不等式，限于篇幅，不再展开论述.

4 加权推广

定理3设ai＞0，pi≥0，pn+i=pi(其中i=1，2，3，…，n，n∈N，n＞1)，，qi＞0(其中i=1，2， 3，…，n，n∈N，n＞1)，，则

证明在不等式(1)中用qiai替换ai(其中i=1，2，3，…n)，得

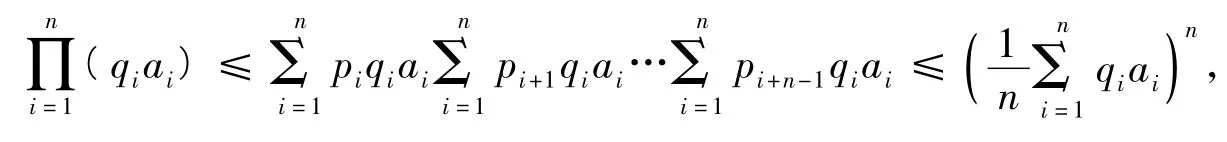
［1］匡继昌.常用不等式［M］.3版.济南:山东科学技术出版社，2004:348-375.