以曲代曲求证一类对称不等式

●张艳宗刘春苗(元济高级中学浙江海盐314300)

以曲代曲求证一类对称不等式

●张艳宗刘春苗(元济高级中学浙江海盐314300)

例1已知x，y，z＞0，且x4+y4+z4=1，求的最小值.

(2000年江苏省高中数学竞赛试题)

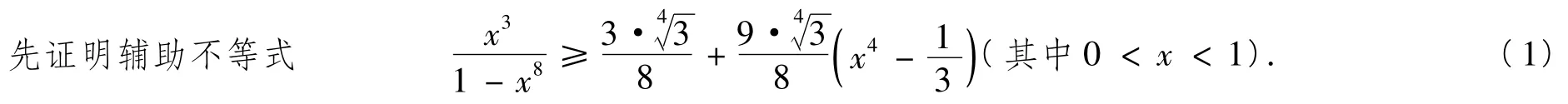
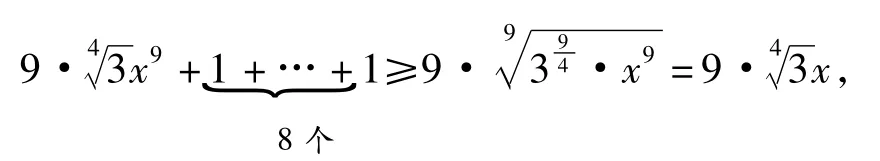
评注此题解法颇多，此处“以曲代曲”虽然没有“占到任何便宜”，计算量也不小，但指出了此不等式的几何意义，也恰是本解法的亮点所在.

例2已知0＜a，b，c＜1，且满足ab+bc+ca=1，求证:

(2004年新加坡数学奥林匹克竞赛试题)

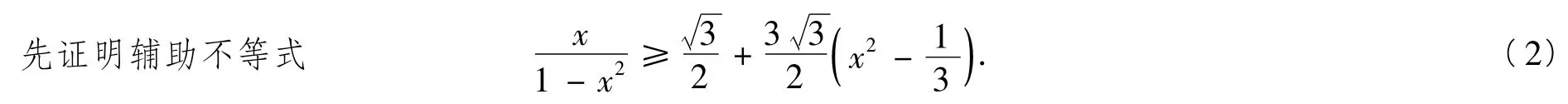
评注将条件适当放缩、改造，创造使用“以曲代曲”有利的外部环境.

例3已知xi＞0(其中i=1，2，…，5)，且，证明:

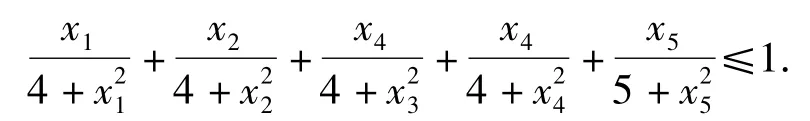
(2003年中国西部数学奥林匹克竞赛试题)

分析不等式中条件式及待证式都是关于x1，x2，…，x5的对称结构，推断当x1=x2=…=x5=4时不等式等号成立.希望找到一个函数g(x)，其图像始终在函数上方，且在x=4处二者相切.不等式右边是常数1，推断函数g(x)中含有，且由条件，可预测函数g(x)中含有λ，即，其中λ为待定系数.由此建立辅助不等式记(其中x＞0)，希望h(x)在x=4时取得最大值0，则，由h'(4)=0，解得

式(3)⇔(x+1)(x2+4)+15(x2+4)≥20x(x+1)⇔(x-4)2(x+4)≥0.最后一式显然成立，即式(3)成立，从而

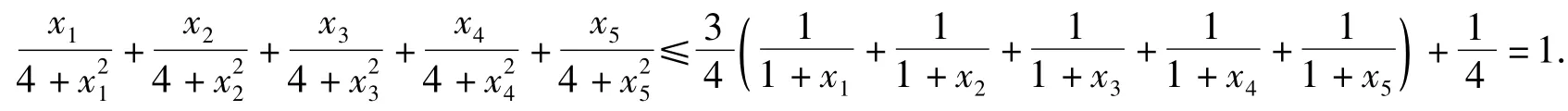
不等式得证.

评注文献［2］通过换元，将非线性约束条件转化为线性约束条件，再构造切线证明，过程稍显繁杂.此处将“切线法”的思想方法迁移，直接构造与函数f(x)相切的曲线g(x).通过几何画板作图易发现，所构造的辅助函数与函数在点处相切，且当x＞0时，函数g(x)的图像在f(x)图像的上方.

(2014年库斯特数学奥林匹克竞赛试题)

证明条件式及待证式都是关于a，b，c的对称结构，推断当a=b=c=1时不等式等号成立.由于，则类似例3分析，引进辅助不等式:(其中，λ为待定系数).记，且h(x)在x=1时取得最大值0，则由h'(1)=0，解得

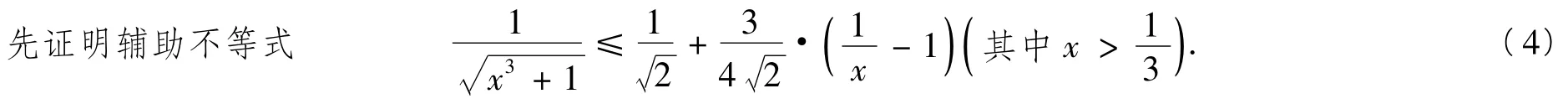
不等式得证.

评注根据不等式等号成立的条件，确定函数f(x)图像上的切点，便于引进辅助函数g(x).

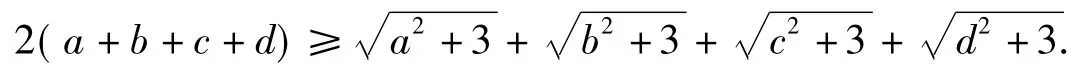
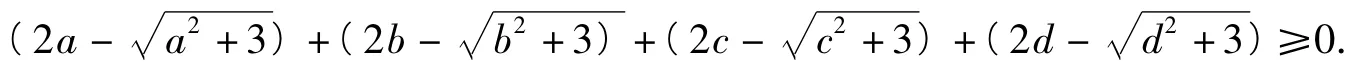
不等式条件式及待证式左边的每一项都是只含一个字母的对称结构，断定当a=b=c=d=1时等号成立.从而建立辅助不等式(其中x＞0，λ为待定系数).记(其中x＞0)，且h(x)在x=1处取得最小值0，则由h'(1)=0，解得

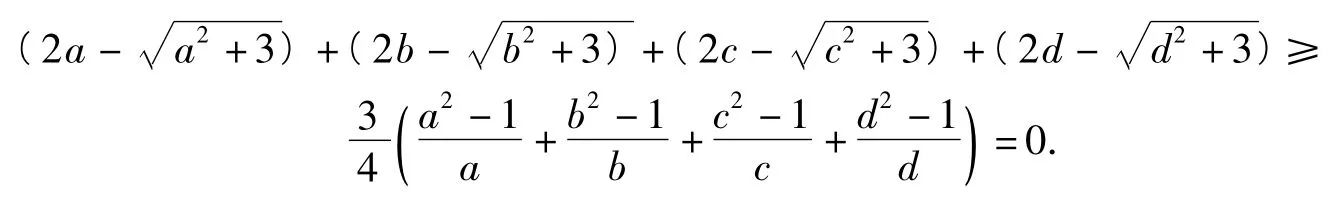
评注独辟蹊径，妙用“以曲代曲”，给人以美的享受.

证明为将条件abcd=1转化为每一项只含一个字母的对称结构，不妨等式2边取对数，得lna+ lnb+lnc+lnd=0.观察不等式，当a=b=c=d=1时，取到等号，引进辅助不等式(其中x＞0，λ为待定系数).记(其中x＞0)，希望h(x)在x=1处取得最小值0，则由h'(1)=0，解得，即

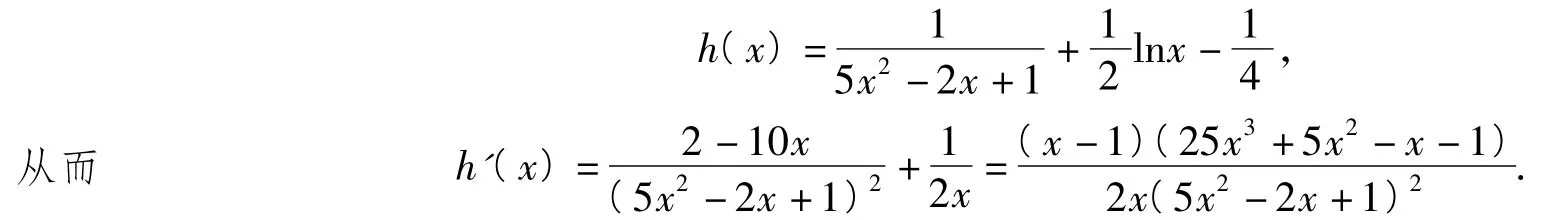
分析可知方程25x3+5x2-x-1=0仅有1个根x0，且当时，h(x)在上递减，在(1，+∞)上递增，且h(x)≥h(1)=0，，即当时，

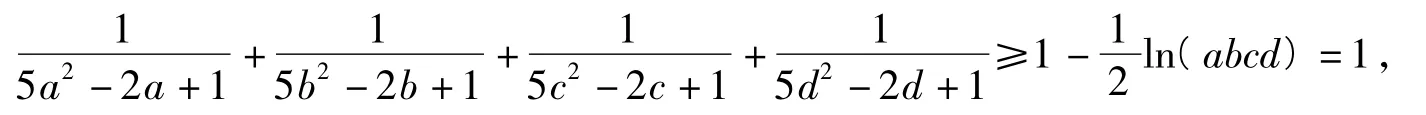
不等式得证.

评注本题难度较大.首先，通过取对数，将变量的乘积形式转化为每项只含1个字母的对称结构，以便利用“以曲代曲”;其次，在构造辅助不等式的过程中发现，辅助不等式对变量的范围有限制，通过分类讨论对变量在不同的范围分别进行证明.

正如文献［1］指出，“以曲代曲”是传统切线法的深化与发展，在处理这类对称性不等式问题上发挥奇效，不但可以优化解题思路，而且有利于沟通函数与不等式等数学知识之间的相互关系，还有利于寻找不等式中隐藏的几何意义.希望有兴趣的同仁加入到研究的队伍中来.

［1］张艳宗，徐佳月.以曲代曲证明不等式——切线法的深化与发展［J］.数学通讯:下半月，2014(10): 24-27.

［2］张宏.利用切线方程证明不等式［J］.中等数学，2009(4):6-12.