2014年高考三视图考点透视
●李志勤李文元齐展修(平邑县第一中学山东平邑273300)
2014年高考三视图考点透视
●李志勤李文元齐展修(平邑县第一中学山东平邑273300)
1 热点透析
三视图是高考必考内容之一,考查几何体的三视图以及与表面积、体积的交汇是高考命题的重点.这类题目通常属中等偏易题,题型多以选择题、填空题为主,有时也会出现在解答题中.近几年高考对三视图的考查更加多元化,如非常规放置的几何体、组合体、几何体的切割问题、在常规几何体中挖出某一几何体等.题目灵活,增加了问题的难度,更能考查学生的空间想象能力.如何快速解决这类问题,首先需要明确这类问题的命题方向.
2 题型分类精讲
2.1 形状的判断
例1在如图1所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别为(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号为①,②,③,④的4个图,则该四面体的正视图和俯视图分别为()
A.①和② B.③和①
C.④和③ D.④和②
(2014年湖北省数学高考试题)
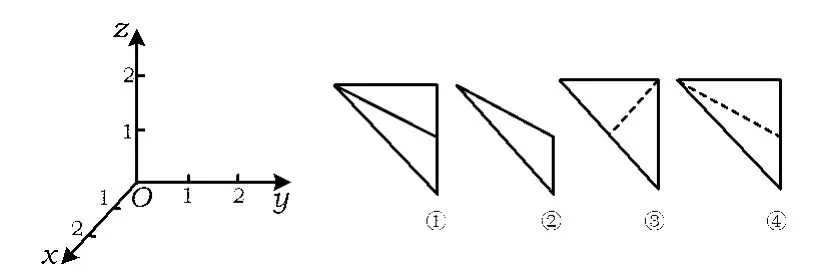
图1
分析在坐标系中,标出已知的4个点,根据三视图的画图规则,可得结论.
解如图2,在坐标系中,标出已知的4个点,根据三视图的画图规则,可得三棱锥的正视图和俯视图分别为④和②.故选D.

图2
点评本题考查三视图的画法和空间想象能力,应做到心中有图,属基础题.
2.2 表面积的计算
例2某几何体的三视图(单位:cm)如图3所示,则此几何体的表面积是()
A.90 cm2B.129 cm2
C.132 cm2D.138 cm2
(2014年浙江省数学高考试题)
分析该几何体是直三棱柱与直四棱柱的组合体,根据三视图判断直三棱柱的侧棱长与底面的形状及相关几何量的数据,判断四棱柱的高与底面矩形的边长,把数据代入表面积公式计算.

图3
解由三视图知:该几何体是直三棱柱与直四棱柱的组合体,其中直三棱柱的侧棱长为3,底面是直角边长分别为3,4的直角三角形,四棱柱的高为6,底面为矩形,矩形的2条相邻的边长为3和4,因此该几何体的表面积为

故选D.
点评本题考查由三视图求几何体的表面积.根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.类似的题目还有2014年安徽省数学高考理科第7题.
2.3 最值问题
例3如图4,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()

(2014年全国新课标数学高考试题)
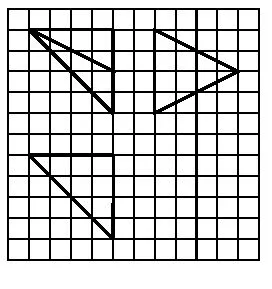
图4
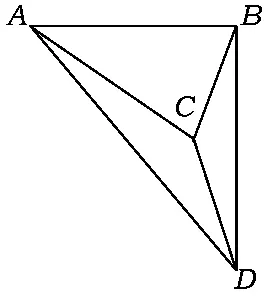
图5
分析画出图形,结合三视图的数据求出棱长,推出结果即可.
解该几何体的直观图如图5所示:AB=4,BD=4,C到BD的中点的距离为4,因此
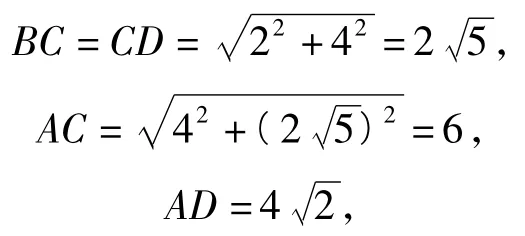
显然AC最长.故选B.
点评本题考查三视图求解几何体的棱长,考查计算能力.类似的题目还有2014年北京市数学高考文科第11题.
2.4 体积计算
例4某几何体的三视图如图6所示,则该几何体的体积为()
A.12 B.18 C.24 D.30
(2014年重庆市数学高考试题)

图6
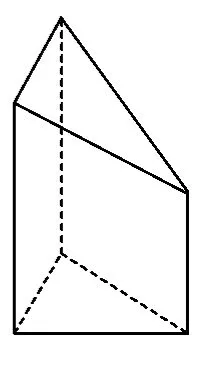
图7
分析该几何体是三棱柱消去一个同底的三棱锥,根据三视图判断三棱柱的高及消去的三棱锥的高,判断三棱锥与三棱柱的底面三角形的形状及相关几何量的数据,把数据代入棱柱与棱锥的体积公式计算.
解由三视图知:几何体是三棱柱消去一个同底的三棱锥(如图7):三棱柱的高为5,消去的三棱锥的高为3,三棱锥与三棱柱的底面为直角边长分别为3和4的等腰直角三角形,因此几何体的体积为

故选C.
点评本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.类似的题目还有2014年辽宁省数学高考理科第7题和天津市数学高考理科第10题.
2.5 证明线面关系、线面角
例5四面体A-BCD及其三视图(如图8所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.
(1)证明:四边形EFGH是矩形;
(2)求直线AB与平面EFGH夹角θ的正弦值.
(2014年陕西省数学高考试题)

图8
分析(1)由三视图得到四面体A-BCD的具体形状,然后利用线面平行的性质得到四边形EFGH的2组对边平行,即可得四边形EFGH为平行四边形.再由线面垂直的判断和性质得到AD⊥BC,结合异面直线所成角的概念得到EF⊥EH,从而证得结论.
(2)分别以DB,DC,DA所在直线为x,y,z轴建立空间直角坐标系,求出点的坐标、及平面EFGH的一个法向量n,用与n所成角的余弦值的绝对值得直线AB与平面EFGH夹角θ的正弦值.
(1)证明由AD∥平面EFGH,AD⊂平面ABD,且平面ABD∩平面EFGH=EF,得

由BC∥平面EFGH,可得EH∥FG,于是四边形EFGH是平行四边形.由三视图知AD⊥平面BCD,又AD∥EF,从而EF⊥平面BCD,于是

因此四边形EFGH是矩形.
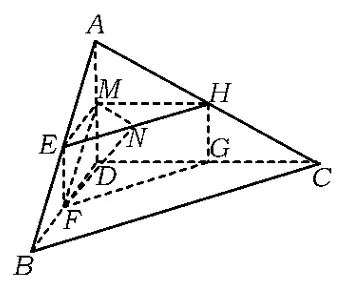
图9

图10
(2)解法1如图9,取AD的中点M,显然ME∥BD,MH∥CD,MF∥AB,且ME=MH=1,平面MEH⊥平面EFGH.取EH的中点N,联结MN,则
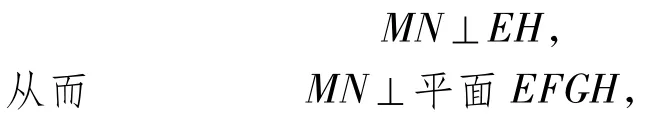
于是∠MFN就是MF(即AB)与平面EFGH所成的角θ.因为△MEH是等腰直角三角形,所以

解法2(向量法)建立如图10所示的坐标系,可得A(0,0,1),B(2,0,0),,F(1, 0,0),G(0,1,0),则

设平面EFGH的法向量为n=(x,y,z),则

取n=(1,-1,0),得
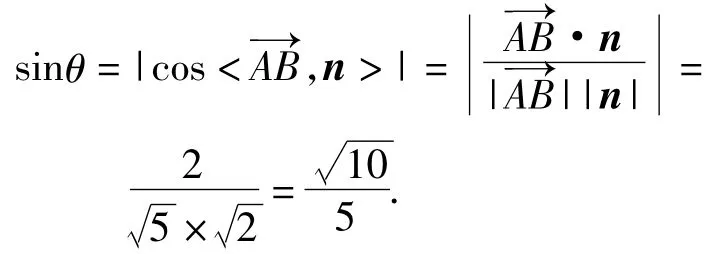
点评本题考查了空间中直线与直线的位置关系、直线和平面所成的角,训练了利用空间直角坐标系求线面角.解答本题的关键在于建立正确的坐标系,求出相关平面的法向量,利用数量积公式求解,属中档题.
3 方法技巧提炼
三视图与传统的立体几何的相关考点整合是命题的趋势.在解决三视图问题时,要掌握三视图的画法;注意符号语言、文章语言、图形语言之间的转化,提高识图、理解图、应用图的能力.在解决三视图的综合问题时,要特别重视三视图给定的信息,要能够准确无误地将三视图中给定的数据信息转化为相应的直观图,以便迅速地找到解题思路.

