关于切点三角形的几个有趣性质

●尚品山(榆林第二实验中学陕西榆林718000)

关于切点三角形的几个有趣性质

●尚品山(榆林第二实验中学陕西榆林718000)

常庚哲先生在1980年第2期的《数学通报》中给出了与内心的切点三角形有关的2个优美不等式.笔者受此启发，对切点三角形的相关性质也进行了一些探索与研究，得到如下结果.

为了叙述简便，文中约定:△ABC与其切点△A'B'C'的边长分别为a，b，c与a'，b'，c';△ABC的面积、半周长、内外切圆的半径及内心到各顶点的距离分别为Δ，s，r，R及R1，R2，R3.

图1

引理1在△A'B'C'中，有

证明略.

引理2［1］在△ABC中，有如下恒等式:

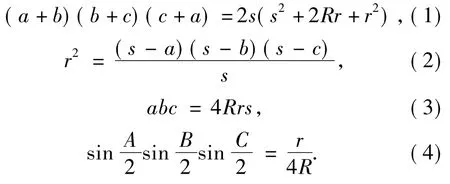
引理3［2］在△ABC中，有如下不等式:

证明根据柯西不等式知

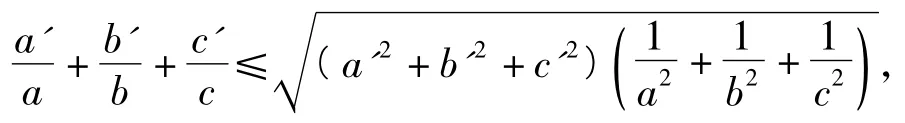
结合式(2)得

而由式(5)可知

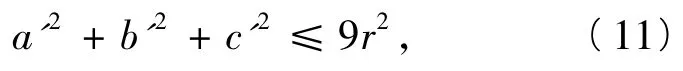
从而由式(10)和式(11)可得

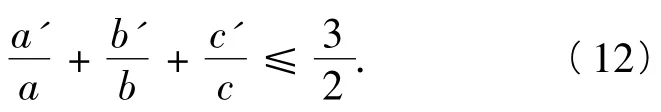
另由海伦公式及半角余弦公式可得

根据均值不等式并结合式(14)，得

从而由式(12)和式(15)即得欲证.

结合式(4)和式(6)，得

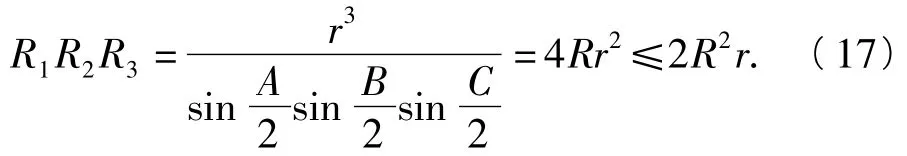
从而由式(17)、式(18)即得欲证.

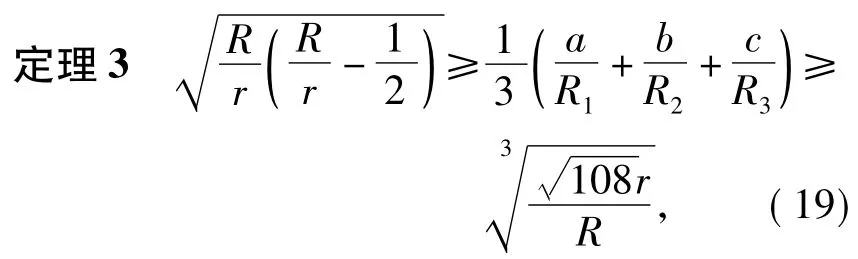
证明根据柯西不等式知

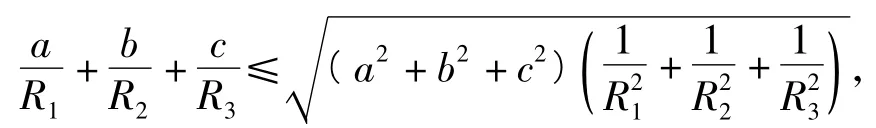
而由定理2的证明过程易知

另由熟知的三角形恒等式

并结合式(4)得

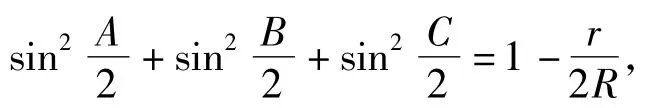
则由式(20)知

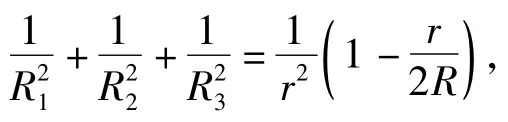
从而利用式(5)有

又由均值不等式并结合式(3)、式(7)、式(17)，得

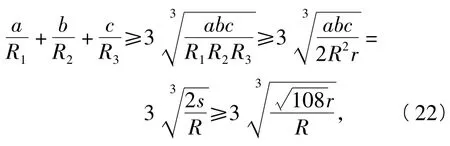
从而由式(21)、式(22)即得欲证.

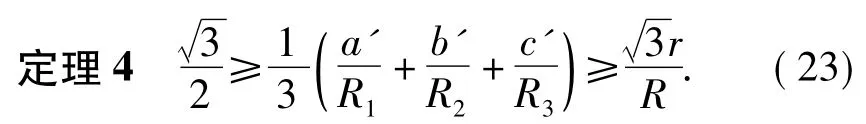
证明由引理1及定理2的证明过程知

从而由式(8)，得

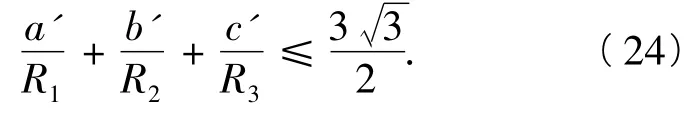
从而由式(24)、式(25)即得欲证.

［1］陈计，叶中豪.初等数学前沿［M］.南京:江苏教育出版社，1996:90-96.

［2］杨世明.中国初等数学研究文集［M］.郑州:河南教育出版社，1992:870-886.