Weideman公式的证明

林谷佳

(重庆师范大学 数学科学学院，重庆 401331)

JAC Weideman曾推测出一个关于调和级数的恒等式[1]：

(1)

要证得该恒等式成立具有一定的难度，以至于它的证明被Chu等人称为组合数学中最难的挑战之一[2-4]，Schneider[5]利用计算机代数包Sigma得到过它的证明，Chu等人利用超几何级数、部分分式法和求导法等也得到了该猜想的证明.受到Chu等人证明方法的启发，笔者利用Dougall-Dixon公式也得到了Weideman调和级数恒等式的证明.

1 预备知识

超几何级数的定义为[6]

2 Dougall-Dixon公式与调和级数恒等式

Dougall-Dixon公式[7]

当(2+a-2b-2c)的实部大于零时公式收敛.

现取a=λx+θy-n，b=λ'x+θ'y-n，c=-n.(其中λ,λ',θ,θ'∈Ζ)得

(2)

(3)

其中

考虑恒等式(3)中x=y=0的情况：

(4)

令

W(x,y)=-(λ-λ')Hk(λx-λ'x+θy-θ'y)-λHk(λx+θy) +λ'Hn-k(-λ'x-θ'y)+λHn-k(-λx-θy);

通过计算可得

DxΛk(x,y)=Λk(x,y)W(x,y);DxU*(x,y)=U*(x,y)Ω(x,y);

DxV*(x,y)=V*(x,y)L(x,y).

将Dx作用于恒等式(3)得

(5)

在恒等式(5)中，当x=y=0时得

将Dx作用于恒等式(5)且取x=y=0得

(6)

其中

而恒等式(6)中Λk(0,0)=U*(0,0)=V*(0,0)=1;W(0,0)=(λ'-2λ)Hk+(λ'+λ)Hn-k;

因此恒等式(6)即为

(7)

现在考虑将Dy作用于恒等式(5)所得的结果，令

DyΛk(x,y)=Λk(x,y)N(x,y);DyU*(x,y)=U*(x,y)M(x,y);DyV*(x,y)=V*(x,y)Q(x,y).其中

则Dy作用于恒等式(5)且取x=y=0所得的结果为

(8)

其中

而恒等式(8)中,Λk(0,0)=U*(0,0)=V*(0,0)=1,N(0,0)=(θ'-2θ)Hk+(θ'+θ)Hn-k;

因此恒等式(8)即为

(9)

通过对比恒等式(7)与恒等式(9),不难发现当恒等式(9)中取θ=λ时得到恒等式(7)，因此恒等式(7)是恒等式(9)的推论.

恒等式(9)中取λ=2λ'≠0,θ=2θ'≠0得

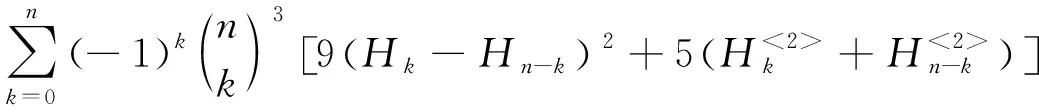
(10)

在Dougall-Dixon公式中取a=-n，b=λx+θy-n，c=λ'x+θ'y-n,得

(11)

(12)

其中

令DxDk(x,y)=Dk(x,y)G(x,y);DxF(x,y)=F(x,y)J(x,y).

其中

将Dx作用于恒等式(12)得

(13)

令DyDk(x,y)=Dk(x,y)R(x,y);DyF(x,y)=F(x,y)S(x,y).

其中

将Dy作用于恒等式(13)且取x=y=0得

(14)

其中

而恒等式(14)中

Dk(0,0)=F(0,0)=1.R(0,0)=(θ'+θ)(Hk+Hn-k);

G(0,0)=(λ'+λ)(Hk+Hn-k);S(0,0)=(θ'+θ)(2H2m+Hm-H3m);

J(0,0)=(λ'+λ)(2H2m+Hm-H3m).

因此恒等式(14)即为

(15)

恒等式(15)中取λ'=θ=1,λ=θ'=0得

(16)

取λ=λ'=θ=θ'=1得

(17)

恒等式(17)减去恒等式(16)的两倍得

(18)

恒等式(10)减去恒等式(18)的两倍就得到了恒等式(1),证明了Weideman的猜想是正确的.

这种对超几何级数恒等式进行参数替换然后求导的方法可以构造或证明出很多组合恒等式，本文只利用了Dougall-Dixon公式，利用Pfaff-SaalschÜtz公式、Kummer公式等也能得出漂亮的组合恒等式.