割补法在三视图还原空间几何体中的应用

安徽省芜湖市沈巷中学

何业亮 (邮编：241012)

三视图是高中新教材新增内容，也是高考的常考知识点．不难发现，由三视图还原几何体的试题经“考”不衰，且其载体的复杂程度呈增加之势，特别是以简单组合体为载体的试题备受命题专家亲睐．虽然很多学生能将“长对正，高平齐，宽相等”烂记于心，也对简单几何体的三视图了如指掌，但处理这类问题仍力不从心，无法可依，甚至不少教师的讲解和很多资料的答案往往是直接告知几何体，不作详细解释．笔者经过深入研究，发现割补法(对三视图进行分割或修补)能有效处理复杂的三视图还原几何体问题，且简单易行，直观明了．

1 合理分割，各个击破

例1(2015·重庆·文5)某几何体的三视图如图1所示，则该几何体的体积为( )

图1

例2(2014·安徽·理7)一个多面体的三视图如图2所示，则该多面体的表面积为( )

解析此题易被正方形中的虚线和实线所迷惑，从而无法得出该多面体的直观图．我们可以将三视图分割成三部分后重新组合，如图2.1-2.3所示．

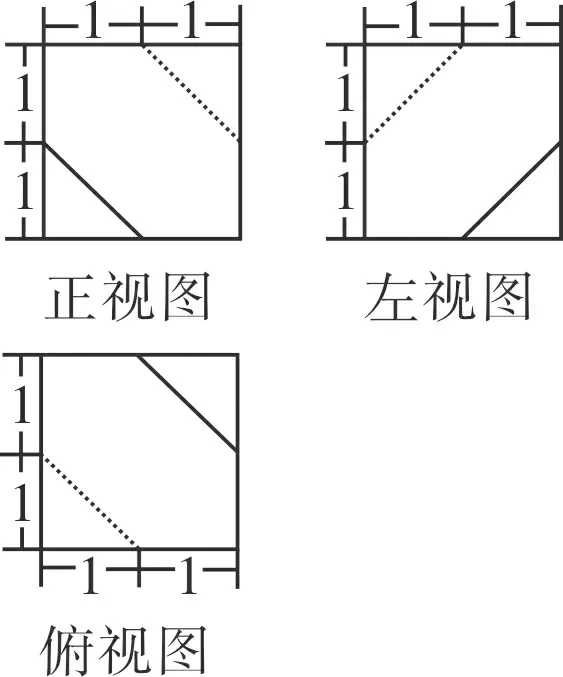
图2

评述在“长对正，高平齐，宽相等”的前提下，可将一些复杂的三视图分割成若干个熟悉几何体或简单几何体的三视图，后将所得的那些几何体进行符合题意的组合，即可得所求几何体.

2 恰当修补，无中生有

例3(2014·重庆·理7)某几何体的三视图如图3所示，则该几何体的表面积为( )

A.54 B.60 C.66 D.72

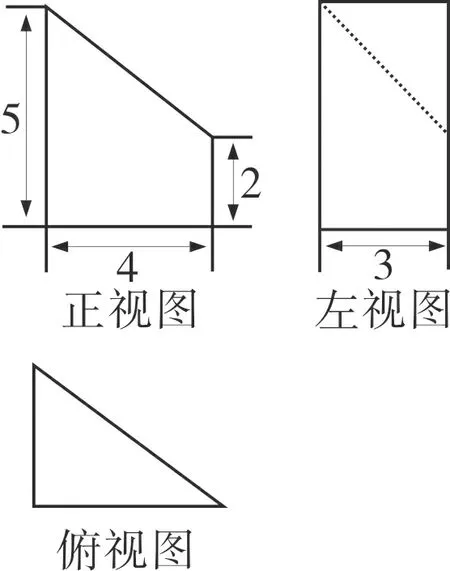
图3

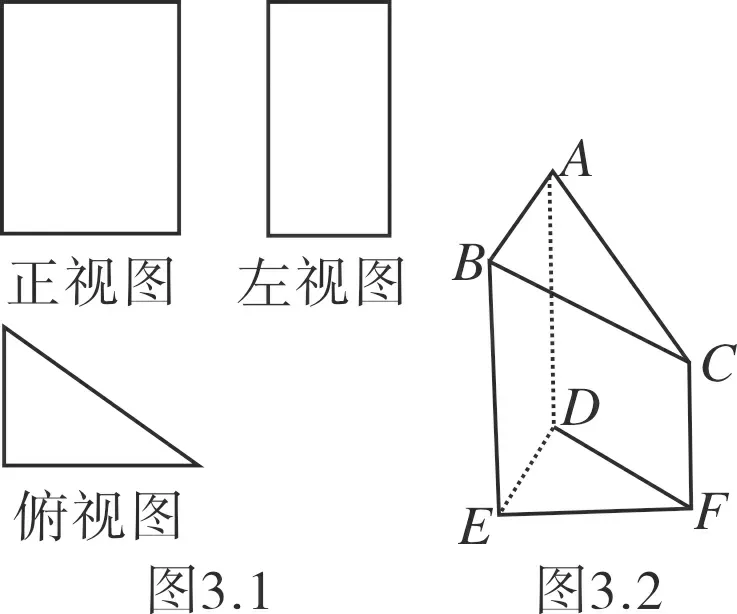
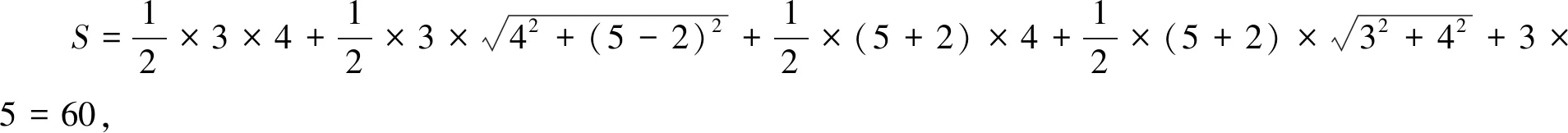
例4(2012·湖北·理4)已知某几何体的三视图如图4所示，则该几何体的体积为( )

图4

评述本着“长对正，高平齐，宽相等”的原则，可将有些三视图修补成一个简单几何体或熟悉几何体的三视图，然后在所得几何体上进行恰当的添补或剪裁，直到得到符合题设的几何体．

3 割补合用，双管齐下

例5(2014·辽宁·理7)某几何体的三视图如图5所示，则该几何体的体积为( )

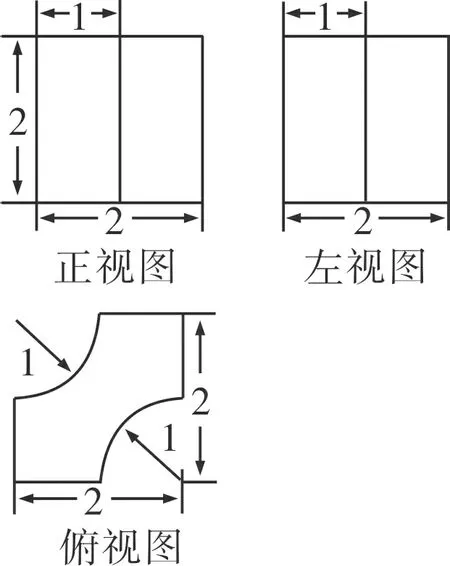
图5

评述有些三视图还原几何体的问题，可对三视图进行分割和修补，这样能有效地转化为熟悉几何体的三视图，但是一定要遵循“长对正，高平齐，宽相等”的原则，否则对后续几何体的确定不利．

由此可见，处理复杂的三视图还原空间几何体问题，割补法有着奇效，可以化陌生为熟悉，化复杂为简单．