高三数学复习课“轨迹方程的求法”的教学与思考

安徽省合肥市第一中学

董 洁 诸 敏 (邮编：230601)

复习课是高三教学中一种重要的课型，主要是帮助学生系统地巩固已学知识，并进行查缺补漏．更重要的是引导学生构建完整而优化的学科知识网络体系，培养学生从更高的视角去思考问题，从而提升学生的思维品质．纵观近几年的高考数学试题，很多题目都是源于课本，而又高于课本的．在复习中，通过对例习题的深入挖掘和知识迁移，“编”出考题，利用发散思维“变”中出彩，使学生对知识进行再现、整合，运用综合、分析、比较、归纳、概括、类比等方法，综合训练逻辑思维能力．让学生从“编”与“变”的探究过程中掌握数学基本方法．

本文以一节高三复习公开课“轨迹方程的求法”为例，通过引导学生回归课本，深入挖掘，鼓励学生“编”出考题，在“变”中出彩，希望对高三复习课的教学有所启发．

1 课堂教学简录

1.1 回归课本，立足基础，唤醒知识

由于本节课是高三第一轮复习课，学生已经学习了曲线与方程的概念，求轨迹方程的基本方法．在课堂一开始，教师便引导学生快速回忆曲线与方程的关系，直接归纳了轨迹方程的求法，揭示了解析几何的本质，即用代数方法来解决几何问题，体现了数形结合的思想，确保轨迹方程的完备性与纯粹性．

教学中，选取了人教A版《必修2》圆的方程第124页习题4.1 B组第2题．长为x≥0,y≥0的线段AB的两个端点A和B分别在x轴和y轴上滑动，求线段AB的中点的轨迹方程.

师：请同学们独立思考，再小组讨论，总结出多种解法．

生1：如图1所示，建立平面直角坐标系，设线段AB的中点x≥0,y≥0，则A(2x,0)，B(0,2y)．依题意知|AB|=2a,代入得x≥0,y≥0，化简得x2+y2=a2．所以线段AB的中点的轨迹方程为x2+y2=a2．

图1

师：这里x、y有限制条件吗？

生1：x≥0,y≥0，则线段AB的中点的轨迹方程为x2+y2=a2(x≥0,y≥0).

师点评这种方法是直接法，通过已知条件，直接列出动点(x,y)的关系式，化简得到动点的轨迹方程．

依题意，线段AB的中点的轨迹方程为x2+y2=a2(x≥0,y≥0).

师点评这种方法是定义法，动点的轨迹满足某条曲线(如圆，椭圆，双曲线，抛物线等)的定义，从而可以直接写出动点的轨迹方程．

所以线段AB的中点的轨迹方程为x2+y2=a2(x≥0,y≥0).

师点评这种方法是相关点法(转移法)，若所求动点M依赖于已知动点而运动，则可将已知动点的坐标x0、y0用所求动点M的坐标x、y表示出来，代入到已知动点x0、y0满足的关系式中，从而求出轨迹方程.

图2

生4:如图2所示，建立平面直角坐标系，设线段AB的中点M(x,y)，过点M作x轴、y轴的垂线分别交于C、D两点.

所以线段AB的中点的轨迹方程为：

x2+y2=a2(x≥0,y≥0)．

师点评这种方法是参数法，根据已知条件，选取合适的参数，建立曲线的参数方程，消去参数，得到动点轨迹的普通方程．此方法要注意参数的取值范围．

同学们通过对课本上习题的思考与探究，立足基础，贴合教材，尝试从不同的角度去解决轨迹方程问题.通过一题多解，加深了对于曲线与方程概念的理解，巩固了轨迹方程的各种求法，帮助学生梳理知识体系，构建知识网络．课后学生还需重视基本技能的训练，熟悉求轨迹方程的各种方法，解题时注意去杂补漏，考虑到轨迹方程的完备性与纯粹性，这样才有利于提高和培养学生触类旁通的思维品质．

1.2 深入挖掘，知识迁移，发散思维

图3

师:请同学们将课本上的这道习题，用数学语言描述出来．

生5:如图3所示，A点、B点分别是射线OM、ON上动点，OA⊥OB，|AB|=2a， 求线段AB中点M的轨迹方程．

师:分析本题提供的信息点，你能从哪些方面进行切入？

生6:A点，B点所在的背景曲线(两射线OM、ON，∠MON=90°)

生7:A点、B点的两个约束条件:

①OA⊥OB(角度定值)；

②|AB|=2a(长度定值).

生8:所求动点的属性(求线段AB中点M的轨迹方程)．

1.3 “编”出考题，举一反三，融会贯通

师:你能分别从以上3个切入点出发，通过改变部分条件，形成新的问题，“编”出新的考题吗？

生9:改变切入点1的条件，“编”出考题(变式1)：已知A点、B点为抛物线y2=4x上异于原点O的两动点，OA⊥OB，求线段AB中点Q轨迹方程．

师:有同学可以解出学生9编出的考题吗？

生10:用参数法：依题，直线OA的斜率存在且不为0，设lOA∶y=kx(k≠0)，

设线段AB中点Q(x,y)，

图4

则线段AB的中点Q的轨迹方程为y2=2(x-4).

师:还有其它的方法吗？

生11:用相关点法：设A(x1,y1),B(x2,y2)，线段AB的中点Q(x,y)．

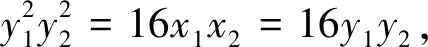
所以4x1+4x2=4y2+32,8x=4y2+32，

即y2=2(x-4)为线段AB的中点Q的轨迹方程．

师:我们能否尝试改变切入点2，切入点3的条件，“编”出不同的考题呢？

教师以上同学的回答非常好，同学们不仅能解出题目，而且也会自己“编”题啦．不过，对于“编”出的题目，还要考查一道新题的严谨性，科学性，简洁性，多去思考出题者的意图，能够举一反三，融会贯通．

1.4 “变”中出彩，发散思维，提升能力

师:除了以上同学提出的想法，老师也来变式出几道题：

变式4 已知线段AB一端点A(4,0)，另一端点B在已知圆O:x2+y2=4上运动，求线段AB中点M的轨迹方程．

变式6 已知长为4的线段AB,一端点A在x轴上，另一端点B在已知圆O:x2+y2=4上运动，求线段AB中点M的轨迹方程．

变式7 (由人教A版《选修2-1》第81页复习参考题B组改编)已知A点、B点为抛物线y2=4x上异于原点O的两动点，OA⊥OB，过点O作AB的垂线，求垂足H点的轨迹方程．

2 课堂教学反思

本节课的设计以课本上的习题为载体，充分发挥教师的引导作用，突出学生的主体地位，让学生经历观察、分析、推理、交流、变式、论证等活动，有利于学生识记、理解和掌握知识．在课堂上，教师要敢于放手，多鼓励学生思考问题，一题多解，一题多变，尊重学生的创新思维，不断挖掘学生的纵向思维和横向思维，注重知识的同化与迁移．

这种新颖的教学方式，对教师的综合素质要求比较高，教师要能够宏观把握整节课的导向、进度及难度，不拘泥于教案及预设，并能统筹安排，因势利导，完成知识的传授和思想方法的渗透．章建跃曾谈到，数学教师的基本任务是帮助学生把一个个具体知识理解到位并能用于解决问题．这恰恰强调了，要培养学生自主学习、交流合作和实际应用的能力．

3 对高三数学复习课的几点思考

3.1 固本浚源，找准切入点

纵观近几年的高考试卷，许多试题在课本中都能找到原型，有的取材于课本中的定理，公理或者公式，有的取材于课本中的例题，习题，即“万变不离其宗”．课本是高考大纲的重要载体，课本具有科学性，示范性，代表性，许多老师和学生在高三复习时往往忽视了课本的重要性，去依赖于大量的辅导资料，信奉“猜题”“押题”，殊不知课本才是高三复习之本．

作为教师，一定要固本浚源，善于钻研挖掘教材，注重教学设计，引导学生梳理知识要点，建构知识体系，总结思想方法．教师可以选择课本上的典型例题或习题作为切入点，重视课本解答过程的严谨性，科学性，去规范我们学生的答题步骤．

3.2 变式探究，激发生长点

许多高考试题是“源于课本，高于课本”的，高三复习课上选择的例题，可以引自于课本，但要有典型性，层次性，灵活性，为学生探究创造提供广阔空间.教师及时发现学生课堂上思维的闪光点，激发高效课堂的生长点，并及时鼓励与评价，启发学生变式探究的能力.变式难度可以循序渐进，变式之间保证思维的连贯与知识的迁移，让学生体会创新的喜悦．鼓励学生推陈出新，融会贯通，举一反三，培养学生归纳，类比，联想，发散，总结的能力，增强学生的数学思维品质，这才是高效课堂的最终目标.