基于运动观点 把握折叠问题本质
安徽省宣城市郎溪县教研室
刘自珍 (邮编:242100)
1 问题的提出
《初中数学教与学》2017年第10期刊登了《山重水复疑无路 柳暗花明又一村》(后称“文[1]”)一文,作者对2016年徐州市一道中考试题(正方形折叠问题)展开课堂教学的探究,挖掘出试题的背景,提炼出求正方形折痕长度的蹊径再推广到求矩形折痕的一般形式.笔者读后受益匪浅,同时认为在解决图形翻折问题时要抓住翻折前后图形的整体特征,抓住翻折问题的核心思想方法,本文在此前提下用运动变化的观点展开探究,却也别有一番洞天.
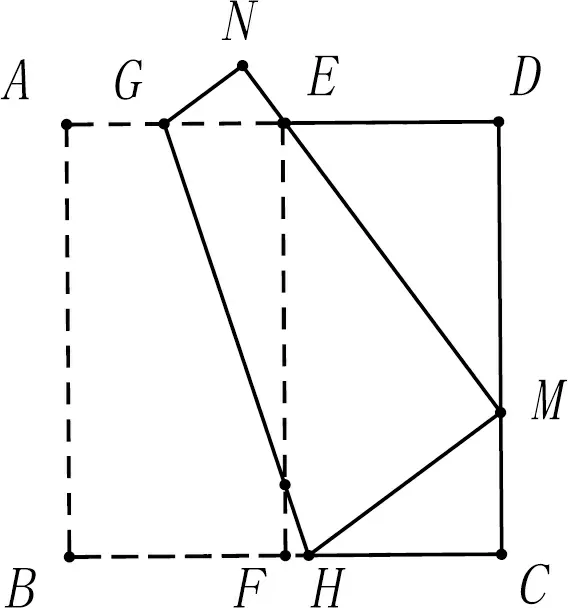
图1

图2
原题已知,如图1,将边长为6的正方形ABCD对折,折痕为EF,展开后再将点B折到CD边上的M处,使边AB过点E,折痕为GH,点A的对应点为N.
(1)若CM=x,则CH=(用含有x的代数式表示);
(2)求折痕GH的长度.
2 翻折问题的核心思想及通法
翻折问题的特点:(1)翻折变换是一种轴对称变换,折痕是对称轴,折痕两侧为全等图形;(2)翻折问题常常伴有直角三角形、中垂线、相似三角形等内容;(3)翻折后生成的图形与原图形构成的图形中有一些特殊的基本图形;(4)翻折变换是一个动态的过程.
翻折问题的核心思想与方法:翻折前后有“变与不变”的规律,方程与函数的思想;
由于翻折问题有着其典型的特征,解题时我们应该着力寻找思考问题和解决问题的通法,这样才能触类旁通、举一反三.
本题通法的思维框图如下[1]
第一次对折:
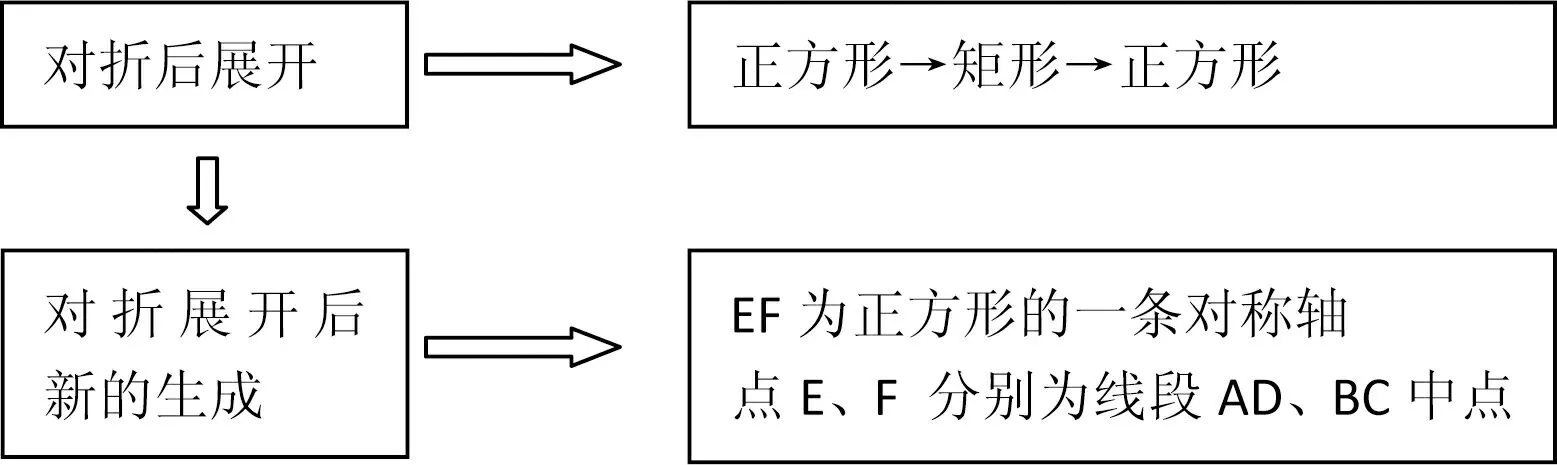
第二次翻折:
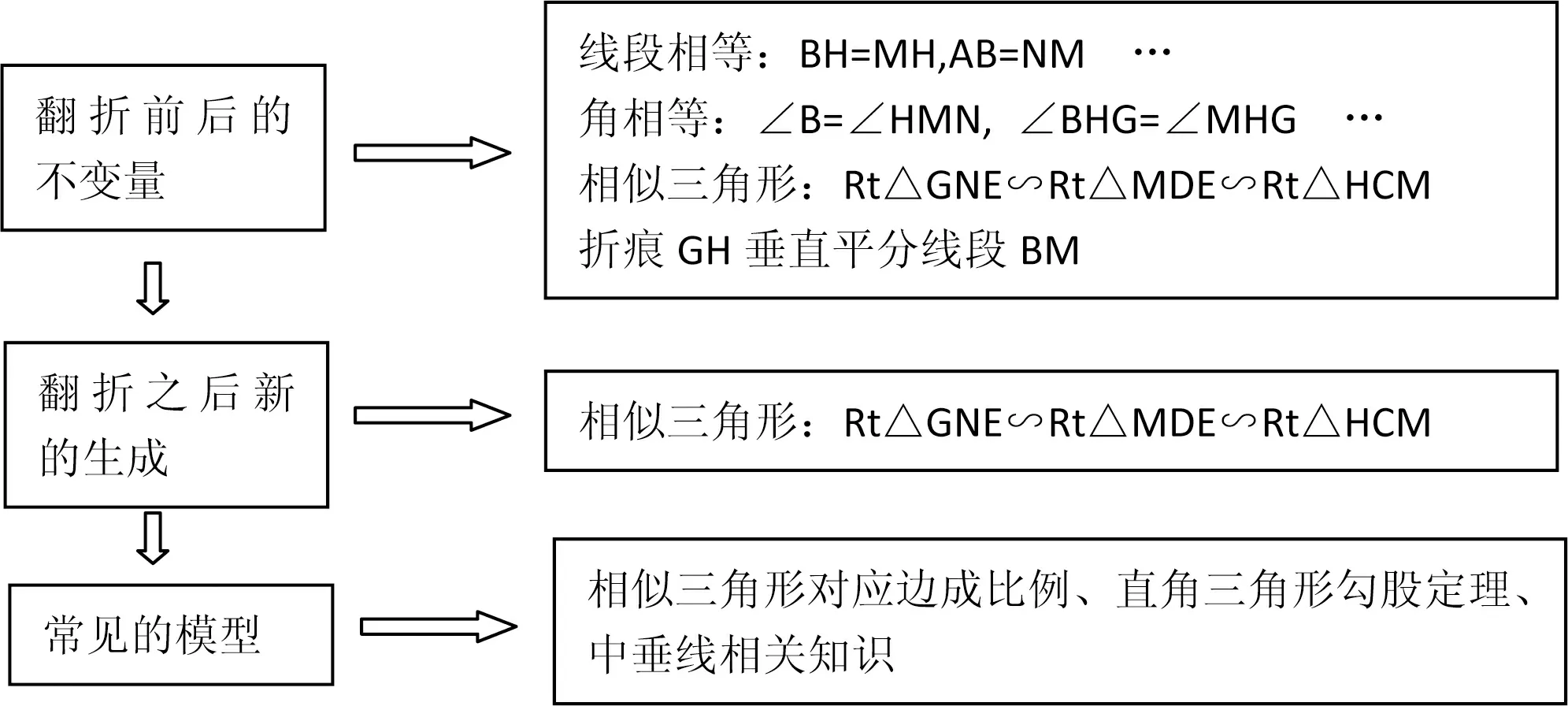
通法解析
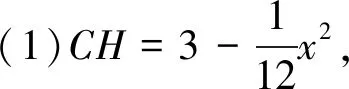

图3
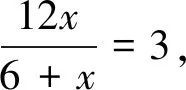
3 基于运动变化的观点展开探究
因为点B折到CD边上的M处,折痕为GH,故可看作是点M在线段CD上移动,导致折痕GH的位置不断地变化及图中的Rt△MDE、Rt△HCM及梯形NGHM的形状都在变化,在变化中是否蕴含某些不变的关系呢?在变化中线段的长短、几何图形的周长、面积是否有内在的变化规律呢?
3.1 点M在线段CD上移动时,探究点、线的特殊位置关系

图4

图5
(1)本题只是M点在线段CD上移动时线段MN过点E的特殊情况,还有许多特殊情况如点M为线段CD的中点,点H为线段FC的中点等;
(2)连接BM,无论M点在线段CD上什么位置,则线段GH、BM、EF三线共点P,且0≤PF≤3,如图4、图5;(易证)
3.2 点M在线段CD上移动(点M不与点C、D重合)时,探究几何图形的内在联系
(3)设线段MN交线段AD于Q点,则Rt△GNQ∽Rt△MDQ∽Rt△HCM;(易证)
(4)设线段MN交线段AD于Q点,无论M点在线段CD上什么位置(C、D点除外),△QDM的周长为定值(正方形ABCD边长的2倍).

图6
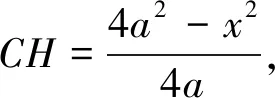
因为Rt△HCM∽Rt△MDQ,
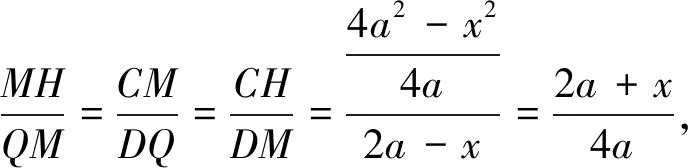

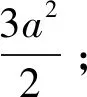



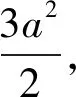
(6)在线段CD上不存在一点M,使得Rt△GNQ、Rt△MDQ、Rt△HCM中任何两个三角形全等;
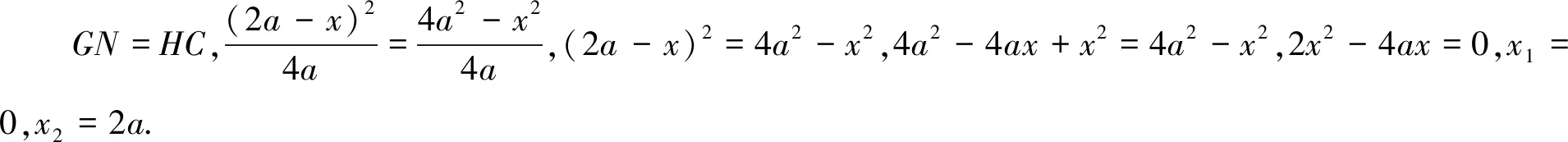

(x-2a)(x+6a)=0,x1=2a,x2=-6a.(两根均要舍去)
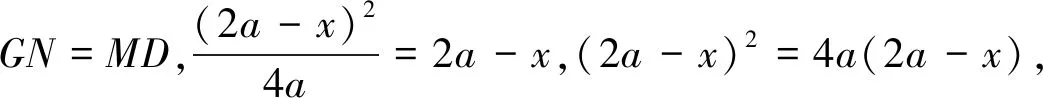
(2a-x)(-x-2a)=0,x1=2a,x2=-2a.(两根均要舍去)
故Rt△HCM、Rt△MDQ、Rt△GNQ三个直角三角形彼此相似,但彼此不全等.
3.3 点M在线段CD上移动时,探究图形线段的内在联系
(7)连接BM,无论M点在线段CD上什么位置,则线段BM=GH.“文[1]”已证;
(8)当点M从C点向D点移动时,线段AG长在减小,但线段BH长度在增加,意味着MC∶DM(或者说MC∶CD)的值与BH∶AG的值有一定的联系.

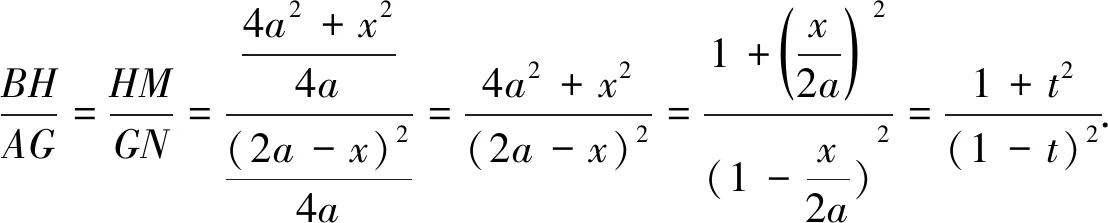
翻折问题是中考试题的常见题型,如矩形的折叠、正方形的折叠、三角形的折叠、圆的折叠等,在解决这一类折叠问题时,要把握翻折变换的核心思想,注意观察折叠前后的有哪些不变的量,研究折叠后有哪些新的基本图形及解决这些基本图形有哪些常用的思想方法,在平时的解题中,可以对某一题进行纵向深入研究,如:探究求折痕长度的办法有哪些?也可以对题目进行横向研究,如本文用运动的观点研究点、线的特殊位置关系和特殊图形的内在联系等.

