动点到动点距离最值的求解策略

上海市松江一中

董顶国 (邮编：201600)

上海市嘉定二中

牟忠智 (邮编：201802)

距离问题为大家熟知，动点到定点距离、动点到定直线距离、动点到动点距离常常成为高考命题的第一视角得到青睐.前两种距离有模式可寻，但对于动点到动点距离，学生颇感棘手.下面笔者对该问题从不同角度进行灵活化归，化“动”为“静”，焕发新的活力.

1 利用反函数图象的对称化归为点到直线的距离

图1

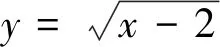
点评该类问题重在从对称中寻求突破，事实上，只要是两曲线(也可能是曲线部分)关于某直线对称，则两曲线上动点距离最值问题通常可划归为一曲线上动点到该线的距离最值问题.

2 利用圆的性质转化为动点到定点距离

图2

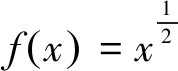
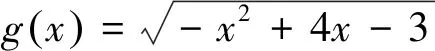
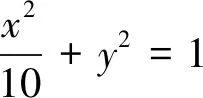
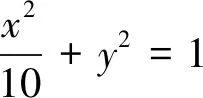
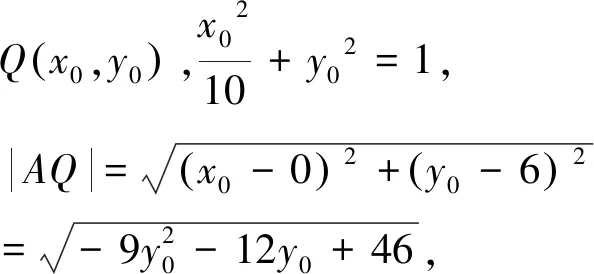
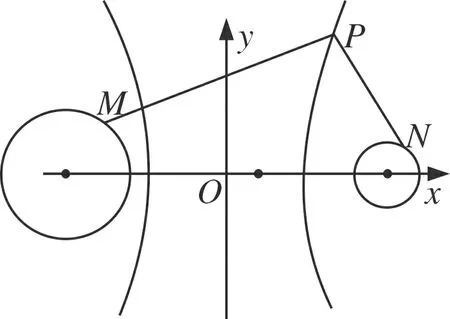
图3

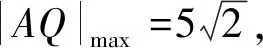
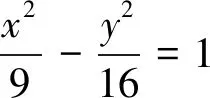
解题分析(|PM|-|PN|)max=|PM|max-|PN|min.设圆(x+5)2+y2=4的圆心为F1(-5,0)，设圆(x-5)2+y2=1的圆心为F2(5,0),|PM|max=|PF1|+2,|PN|min=|PF2|-1，所以(|PM|-|PN|)max=|PM|max-|PN|min=|PF1|+2-(|PF2|-1)=(|PF1|-|PF2|)+3=9.

点评该类问题的核心是利用圆的几何性质，把两动点距离划归为动点到圆心的距离问题，减少了变量个数，简化了思考过程.

3 利用线的平移化归线与曲线关系

图4

(Ⅰ)写出曲线C的参数方程，直线l的普通方程；(Ⅱ)过曲线C上任一点P作与l夹角为30o的直线，交l于点A，求|PA|的最大值与最小值.

(Ⅱ)作PH⊥l于点H，|PA|=2|PH|，|PA|的最值问题即|PH|的最值问题，最值点P即为与l平行的椭圆切线的切点，|PA|的最值化归为切线与直线l的距离问题.

设切线方程为y=-2x+m，带入椭圆方程得25x2-16mx+4m2-36=0.

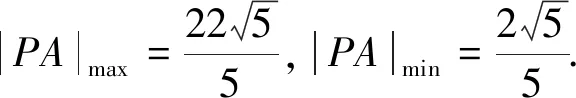
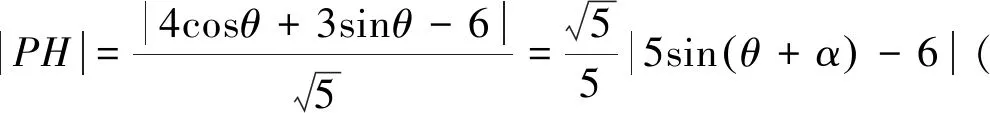
4 利用动点“依托”关系，建模化归函数最值

较多的问题中两动点不是随意变化，而总是存在某种依存关系，利用这种依存关系，恰当引入变量建模求解.

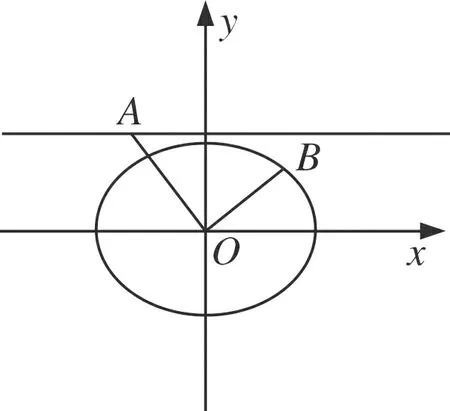
图5

例4(2014北京高考卷)已知椭圆C:x2+2y2=4.

(1)求椭圆C的离心率；(2)设O为原点，若点A在直线y=2，点B在椭圆C上，且OA⊥OB，求线段AB长度的最小值.

(2)设点A、B的坐标分别为(t,2),(x0,y0),其中x0≠0.

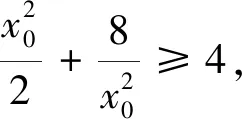
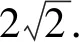
点评该问题通过动点坐标关系的建立，减少参量个数，利用曲线方程中的坐标关系代换，借助曲线范围，较好构建函数模型求解.再如：

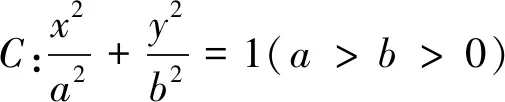
(I)求椭圆C的方程；(Ⅱ)求线段MN的长度的最小值；(Ⅲ)略.

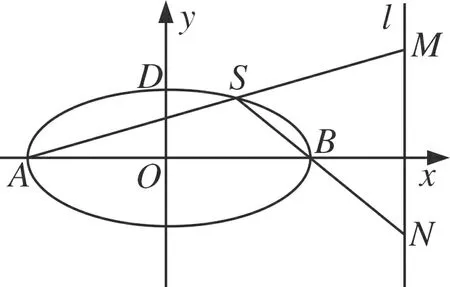
图6

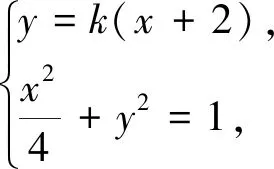
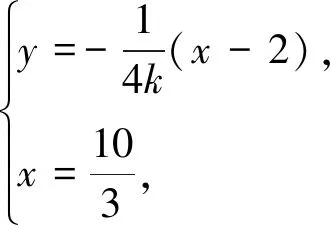
点评该问题中动点距离虽受曲线上动点的直接制约，但动点均为线线交点，结合实际问题，恰当的引入AS的斜率k,构建关于k的函数简捷求解.

5 借助导数工具，寻求转换条件

对于分别在两函数图象上的动点，其距离的常见转化无法实施时，常借助导数这一工具，化归切线间的距离求解.