高考立体几何解答题复习的深度思考
浙江省慈溪实验高级中学
许建芳 (邮编:315300)
数学家波利亚在《数学与猜想》中提到:“数学有两个侧面……用欧几里得的方式提出来的数学是一门系统的演绎科学;但在创造过程中的数学却是实验性的归纳科学.”不同的推理形式有不同的特点和功能,要注意他们之间的有机融合.通过立体几何的学习,学生能掌握逻辑推理的基本形式,学会有逻辑地思考问题:能够在比较复杂的情景中把握事物发展的脉络;形成重论据、有条理、合逻辑的思维品质和理性精神,增强交流能力.通过立体几何的学习,学生能提升数形结合,发展几何直观和空间想象能力;形成数学直观,在具体的情境中感悟事物的本质.立体几何是高中数学的重点,也是高考命题的热点,分析历年高考的立体几何解答题,这就要求在课堂教学中要提升学生的直观想象和逻辑推理的核心素养.
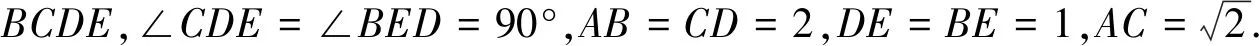
(Ⅰ)证明:DE⊥平面ACD;
(Ⅱ)求二面角B-AD-E的大小.

图1


图2

设平面ADE的法向量为m=(x1,y1,z1),平面ABD的法向量为n=(x2,y2,z2),
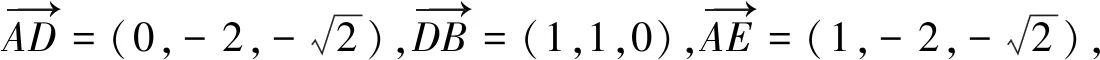







如果我们的课堂教学只关注学生能否解决此问题和学生解题的速度和正确率,长此以往,学生往往为了解题而解题,因为手上的题目很多,要做的就是赶紧把题目都解答出来.在这样的压力下,学生会按照最熟悉的路径去执行,用最熟练的方式去解决问题——简而言之,就是路径依赖.因为只有这样,才能快速腾出手来,去做下一个题目.慢慢的,学生会开始感觉到,没有时间去深入思考.
这会导致学生在自己熟悉的领域,变得越来越熟练,但从来没有真正突破原有的水平,只是成为了一个解题机器,并没有提高素养,其视野很狭窄.只是在解题的时候,一味追求快速解题,让自己像齿轮一样跑起来,让解题走在思维前面——经过长时间的强化,所固化下来的结果.
这种模式,本质上,是无法真正提升核心素养的.因为学生只是一直在重复演练.在这种情况下,边际效用是非常低的,这就是课堂效率低下的症结所在.只有从多视角去看待问题,思考解决此问题的不同方法,讲明用这种方法解决问题的缘由,才能提高学生的核心素养.
方法二(定义法):作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连结BG,由(Ⅰ)知,DE⊥AD,则FG⊥AD,

图3
所以∠BFG是二面角B-AD-E的平面角,在直角梯形BCDE中,由CD2=BD2+BC2,得BD⊥BC.
又平面ABC⊥平面BCDE,得BD⊥平面ABC,从而BD⊥AB.

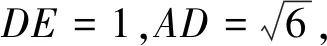


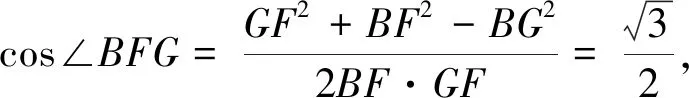

图4



图5
方法四(三垂线法):由(1)知BD⊥BC,所以BD⊥平面ABC.
所以平面ABD⊥平面ABC,取AB的中点M,所以CM⊥平面ABD.
延长DE至F,使得DE=EF,则DC=DF.故点F与点C到平面ABD的距离相等.


图6
方法五(面积射影法):取DC的中点H,则BH⊥平面ADC,设二面角B-AD-C的平面角为θ,


方法六(三面角余弦定理):
设α=∠BDE,β=∠ADB,γ=∠EDB,二面角B-AD-C的平面角为θ.

方法一(坐标法)因为此题有面面垂直的条件,由面面垂直的性质定理可以做出面的垂线,故较易想到建立空间直角坐标系,用坐标法解决此问题.方法二(定义法)分析构成两个半平面的几何图形的几何特征,过公共棱上的一点在两个半平面内分别作出与公共棱垂直的直线,这样就得到了二面角的平面角,此法就是用定义法作出二面角的平面角.方法三(三垂线法)用三垂线法作出二面角的平面角,先要找到其中一个平面的垂线,这样就可以做出二面角的平面角.方法四(三垂线法)在法三的基础上,利用“直线与平面相交,若平面两侧的斜线段长相等,则垂线段长相等”这一几何直观,不需要作出二面角的平面角,就能解决问题,从而简化解题过程.方法五(面积射影法)与方法六(三面角余弦定理)为解决二面角的平面角提供了不同的解题思路.尤其在一些二面角的难题中,当其他方法无效时,不妨用这两种方法去尝试一下.在选择填空中,可以不作出二面角的平面角,就能较快地得到答案,起到事半功倍的效果.
我觉得立体几何的教学中要遵循以下三原则:在直观感知和操作确认的基础上建构空间想象;在思辨论证和度量计算的基础上培养逻辑推理;在深度学习和深度思考的基础上提升核心素养.
教师在教学中要有钻研精神,遇到问题不能浅尝辄止,应该考虑其他各种解法,解法是否具有通性通法,通过一题多解,帮助学生建构起知识网络,更好地掌握解决问题的思路.教师在此过程中要引导学生分析不同解决思路的异同,通过一个问题彻底理解一类问题,让学生在掌握基础知识和基础技能的同时,感悟基本思想方法,积累基本活动经验,提升和发展学生的数学核心素养.

