对一道导数试题的深入探究
安徽省合肥市第二中学
黄 鑫 (邮编:230022)
1 原题再现
2019年4月合肥一中高二期中考试数学试卷第12题如下:
已知函数f(x)=a(x+1)ln(x+1)-x2-ax(a>0)是减函数,则实数a=( )
该题题干简约,解法灵活多样,深入考查了函数的单调性、极值或最值、恒成立问题,对数形结合、转化与化归、分类讨论的数学思想方法有深入的考查.本题作为选择题的压轴题,有较大难度,从学生解答情况来看,得分率也很低.经研究发现,本题与2019年合肥市高三二模第21题第一问是一样的,显然这对高二学生要求较高.本题先把函数f(x)是减函数转化为f′(x)≤0恒成立,下面对该题做进一步探究.
2 解法探究
思路1 转化为求f′(x)的最大值问题
解法1f(x)的定义域为(-1,+∞),f′(x)=aln(x+1)-2x.
由f(x)是减函数得,对任意的x∈(-1,+∞),都有f′(x)=aln(x+1)-2x≤0恒成立.
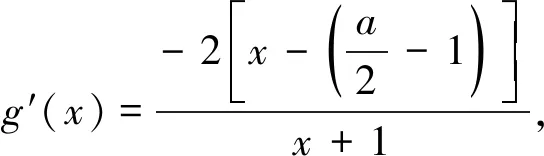


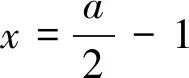
又g(0)=0,故对∀x∈(-1,+∞),g(x)≤g(0)恒成立,即g(x)的最大值为g(0).
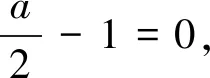
思路2 变量分离,转化为求f′(x)的最大值问题
解法2 由f(x)是减函数得,f′(x)≤0恒成立,即aln(x+1)-2x≤0在(-1,+∞)内恒成立.从而有:当-1 ① ② 记h(x)=(x+1)ln(x+1)-x,则h′(x)=ln(x+1). 所以当-1 故[h(x)]min=h(0)=0,所以当x>-1时,h(x)≥0,从而g′(x)≥0,所以g(x)在(-1,+∞)内是增函数. 由①,得a≥g(0)=2,即a≥2. 由②,得a≤g(0)=2,即a≤2. 综上可得,a=2. 思路3 转化为两个函数比较大小问题,再利用数形结合 上述探究给出了处理此类问题的三种思路,对处理类似问题有较好的借鉴作用.一般情况下,对于含参函数是单调的,往往要求参数的取值范围,本题很有意思,仅在a的一个取值处函数是减函数,这样的函数还有哪些?值得进一步探究.在实际教学中,我们要借助对典型问题的深入研究,达到对数学知识、方法的触类旁通,切实提高教学的有效性,使数学核心素养落地生根.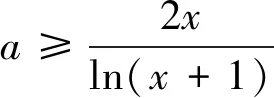
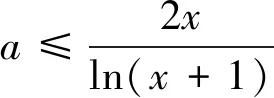



3 教学启示

