巧设情境搭平台适时点拨引生成——以“三角形内角和定理”的证明为例

☉湖北省宜昌市夷陵区教研中心 高先敏

☉湖北省宜昌市夷陵区三峡初中 王超

巧设情境搭平台适时点拨引生成
——以“三角形内角和定理”的证明为例

☉湖北省宜昌市夷陵区教研中心 高先敏

☉湖北省宜昌市夷陵区三峡初中 王超

一、案例背景

教材文本中的几何定理证明，其思想方法带有典范作用.教师应该足够重视，引导学生加以推导证明，在推导证明的过程中，使学生真正掌握所蕴含的数学基本思想和方法.事实上，很多定理的运用，解决问题的途径，都是从定理证明的思想方法中迁移过来，具体解法都渗透了基本思想方法.因此，教师在“定理证明”这一环节中，要重视这方面的挖掘运用与提升，使学生重视定理的证明，防止学生重“结论”轻“过程”的不良学习态度，提高学生的数学素养、思维品质以及学生的学习兴趣.

因此，在几何定理的证明中，教师巧设情境，搭建利于课堂生成的平台；教师适时点拨，不仅可以内化基本的思想方法，同时也通过点拨引领学生思考，生成新的解题思路与方法，同时为学生质疑引导方向.因此，设计“三角形内角和定理”的证明这一环节是非常有必要的.

课堂教学不再是教师按照预设的教学方案机械地、僵化地传授知识的线性过程，而是根据学生学习的实际需要，不断调整、动态生成的过程，教学过程是“精心预设”在课堂中的“动态生成”的过程.

二、案例主题

本案例以几何定理——“三角形内角和定理”的证明为素材，探讨教师如何预设情境，为学生的课堂生成搭建平台；选择合适的时机与方式点拨，引导学生质疑的方向，从而生成教学中的“意外”.把教材用活，把学生教活.

三、案例描述与分析

1.内容分析

“三角形内角和定理”这一内容，上承平行线的判定与性质，下启外角、多边形的内角和.这一内容是几何学习的核心知识点、基础知识点.它的推导，是建立在学生学习了平行线的性质与判定之后，由180°角联想到同旁内角、平角，利用平行线的性质与判定转化、构造.对学生的知识迁移能力、转化思想、数形结合思想的培养起到了很重要的作用.

定理的推导证明方法是重点，教师如何引导学生获取推导的方法以及感悟其中的重要的数学思想与方法是难点.

2.巧设情境搭平台

情境：制作一个三角形纸片，请你用剪、拼的方法说明三角形的内角和为180°.

学生小组分工协作，学生竞相展示拼接的方法，互相补充质疑：“我还可以这样拼”“你这样拼不对”“这样拼也是对的”，这样兴奋的表达语，不绝于耳.

【分析】通过情境1的设置，教师引导学生制作一个生活中的模型，通过实物去剪、拼，让抽象的数学思维情境化、具体化.调动了学生的学习兴趣，打开了思维的空间.

同时，通过这一活动，为下一步进行理论证明，提供了实物模型，指引了思路与方法.

3.适时点拨引生成

如果不用剪、拼的方法，可以用推理论证的方法来说明内角和为180°吗？带着这个疑问，进入了理论的证明.教师在理论证明这一环节中，适时点拨，为学生的质疑引导了方向，打开了思路，从而生成了新的思路与方法.同时，又来源于教材，高于教材，把教材用“活”，把学生教“活”.

（1）由180°想到了什么？

师：三角形内角和为180°，何为180°？由180°想到了什么？

生1：平角.

（同学们点头表示同意.这时，又一个声音响起）

生2：还有同旁内角.

（同学们恍然，有人低声回应“对哟！还有同旁内角”.突然，耳畔又有一个声音）

生3：这个回答不准确，必须是两平行线所截形成的同旁内角.

（这时，很多学生点头表示赞同）

【分析】在剪、拼活动之后，设置问题：“由180°想到了什么？”通过学生的质疑补充，学生脑海中呈现出理论证明内角和定理的方法：（1）构造平角；（2）利用平行线构造同旁内角.

（2）有多余的.

学生通过剪、拼模型，迅速得到两种思路.生1：过顶点A作对边BC的平行线（如图1）.生2：延长BC，过顶点C作对边AB的平行线（如图2）.

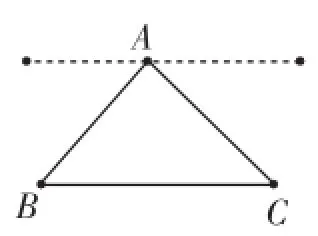
图1

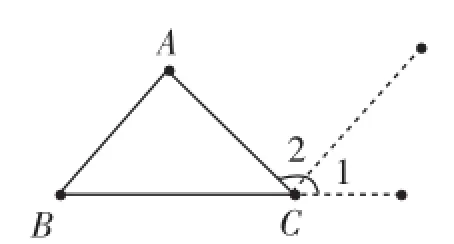
图2

（学生规范地完成理论证明之后，一个学生提出了新的看法）

生3：辅助线有多余的.图2中，只需过C点作AB的平行线.

（学生仔细分析之后，又提出了新的看法）

生4：图1也可以简化，只需过A点作BC的平行射线.

【分析】学生在充分自主完成理论推导的基础上，高度自主、自觉参与活动之中，有了新的认知，故而提出了质疑.因此，在授课中，一定要给学生更多的时间去支配.一是更进一步落实；二是让学生在充分自主的基础上，打开思路，勤于思考，敢于质疑，才能生成更好的资源.

（3）如何转化.

师：上述四位同学是如何将内角和转化的？

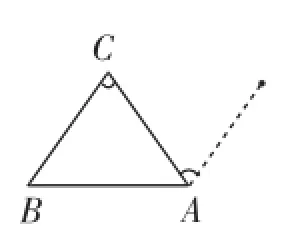
图3

生5：第一位同学，是过顶点A作平行线，将内角和转化为平角.

生6：第二位同学，是延长BC，过顶点C作平行线，将内角转化成一个平角.

生7：第三、四位同学的方法，均是过顶点作平行射线，利用平行线的性质，将内角转化为两平行线所截形成的同旁内角.

师（点拨）：这四位同学，都是通过过顶点作平行线的方法，将内角和转化为平角或同旁内角.

【分析】教师通过引导学生及时归纳梳理，适时点拨，提炼出基本的数学思想与方法，过某一点作平行线，构造平角或同旁内角.为生成其他方法作铺垫

（4）其他点可以吗？

师：前四位同学都是过顶点作平行线，那么其他点可以吗？

学生摆弄模型，得到方法3.

生1：在BC边上取一点D，过D点分别作AB、AC的平行线（如图4）.

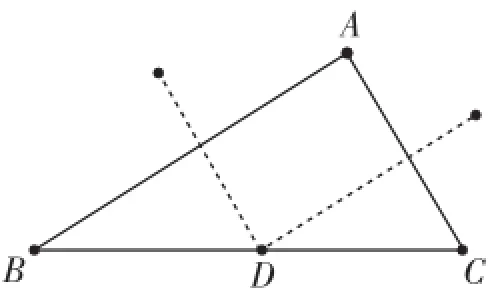
图4

师：还有吗？

生2：在三角形内部取一点，分别作两边的平行线（如图5）.

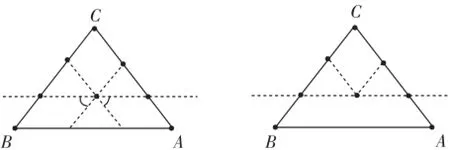
图5

（由于图形复杂，学生陷入了思维障碍）

师（点拨）：作平行线的目的是将三内角转化为一个平角.因此，构造一条或多条直线.（在充分完成理论证明之后）师：还有吗？

生3：在三角形外部取一点，采用类似的方法（如图6）.

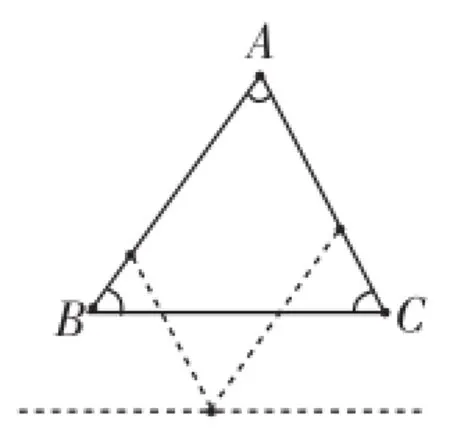
图6

【分析】教师在学生摆弄模型、充分证明的基础上，提出“其他点可以吗？”“还有吗”等引导性过渡语，加大师生间的互动，为生成新的资源指引方向.同时，在学生证明过程中发生思维障碍时，适时、及时点拨，为生成新的资源提供可复制的方法与策略.

四、案例反思

（1）“由180°想到了什么？”问题具体而适中，为学生指引了方向，从180°入手，构造平角或同旁内角.同时，这一点拨放在剪、拼活动之后，在学生有实物感知与具体表象相结合的基础上，在直观的感知下，生成新的数学模型.

（2）“如何转化？”针对具体方法，及时归纳提炼，渗透所蕴含的数形结合思想、转化思想，提炼出构造法等基本数学思想与方法.为其他点的证明提供理论依据以及导引作用.

（3）“其他点可以吗？”问题具体而又带有发散性.在方法的归纳提炼之后，学生的思路完全被打开.同时，加上有实物模型，学生动手动脑，不是纯粹的听、写、记，学习兴趣在授课中得到保持并敢勇于质疑、探究.同时，也为方法的生成、同学间的质疑指引了方向与思路.

巧设合适的情境，激发学生的求知欲，同时，为学生的质疑提供良好的学习氛围，为新知识或方法提供具体的表象，便于理解抽象的素材.本节课，通过剪、拼的方法，学生认识到可以拼在边上、顶点处，便于学生生成.

适时点拨.选择合适的时机、合适的方式，提出具体而不空洞的问题（串），问题富有开放性、包容性和针对性，作为导引，能有效地激发和导引学生进行思维活动，为生成新的资源引路构思.

在以后的课堂中，尽量做到：（1）创设合适情境，让实物模型与数学模型有机结合，使得学生从具体表象中感知数学模型的魅力，体验数学中的美，为新的资源生成搭建平台；（2）多提出一些具有开放性、包容性和针对性的“弹性问题”，启发引导学生进行思维活动，把学生“教活”；（3）多留下一些弹性时空，让学生在高度自觉、充分自主的基础上，主动学习，从而激活学生的发散性思维；（4）适时点拨，点拨所渗透的思想方法，点拨思路受阻的易混点，从而去启发学生寻找新知识的生长点，生成新的教学资源.Z