从函数概念出发：锐角三角函数的生长点

☉江苏省无锡市金星中学 萧婷 朱宸材

从函数概念出发：锐角三角函数的生长点

☉江苏省无锡市金星中学 萧婷 朱宸材

我们注意到，最新的人教版教材九年级下册“锐角三角函数”从一个“生活问题”引入，这种数学新知识的教学都想方设法从“生活现实”引入的努力虽然反映了数学来源于生活、服务于生活的价值取向，然而这个情境的设置其基本目的只是为了复习“在直角三角形中，30°所对的直角边长等于斜边长的一半”这一性质，而直角三角形的这个性质学生在八年级学习等边三角形时就早已熟知了.笔者最近在观摩全国著名特级教师李庾南老师“锐角三角函数”起始课教学视频时发现，李老师放弃了课本提供的情境引入，而是基于学生对直角三角形的已有认知，选择从函数概念出发定义了锐角三角函数，整节课自然亲切，过渡平滑，追求了知识生成中的“逻辑连贯、前后一致”（章建跃语）.本文记录该课的教学过程，与更多同行分享研习.

一、“锐角三角函数”起始课教学过程

（一）研究直角三角形中边、角之间的关系，建构锐角三角函数的定义1.回顾直角三角形中边、角之间的关系

如图1，在Rt△ABC中，∠C＝90°，AC＝b，BC＝a，AB＝c.

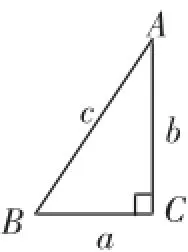
图1

边：a2＋b2＝c2（勾股定理）.

角：∠A＋∠B＝90°（三角形内角和定理推论——直角三角形中两锐角互余）.

2.探讨直角三角形中边与角之间的关系

（1）当锐角∠B大小不变时，Rt△ABC的三边可以变化（如图2）.探究变中之不变——每两边的比值不变.

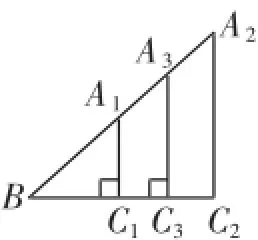
图2

（2）当锐角∠B大小改变时，例如由原来的30°变化为45°时，每两边的比值也改变了，∠B＝60°时，比值又随之改变.所以在直角三角形中，当锐角的大小变化时，直角三角形的每两边的比值也随之变化，且当锐角每取一个确定的值时，三边中的每两边的比值都有唯一确定的值与之对应.

（3）在直角三角形中，锐角与三角形的两边的比值之间是函数关系.

（4）由函数的定义：在某一变化过程中有两个变量x、y，当x每取一个确定的值时，y都有唯一确定的值与它对应，y叫做x的函数，x叫做自变量，可以知道是∠B的函数，∠B是自变量，这就是本课研究的课题：锐角三角函数.

（二）创设情境，观察思考，定义锐角三角函数的概念和互余两锐角的三角函数关系式

1.把直角三角形中的锐角与每两边的比之间的关系给定名称

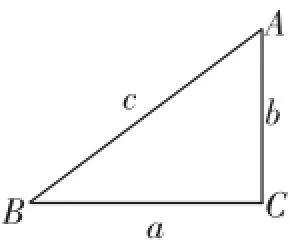
图3

2.符号表示

∠A的正弦记作sin∠A；∠A的余弦记作cos∠A；∠A的正切记作tan∠A.

记号里习惯省去角的符号“∠”，如sinA.如图3，在Rt△ABC中，∠C＝90°，三边分别记作a、b、c.

请思考：

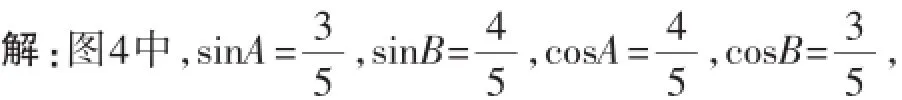
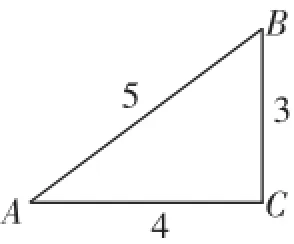
图4

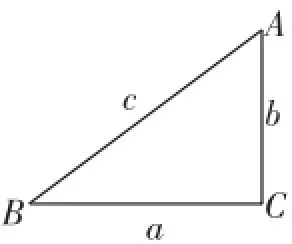
图5

（2）∠A和∠B互余，通过思考（1），有什么发现？

任意锐角的正弦值（余弦值）等于它的余角的余弦值（正弦值），这个关系可用下列式子表示（0°＜α＜90°）：sinα=cos（90°-α），cosα=sin（90°-α）.

（三）根据直角三角形的边和角的性质以及三角函数的定义，引导学生自主探究归纳列出30°、45°、60°的三角函数值表

（1）如图6，在Rt△ABC中，∠A=30°，研究30°的三角函数值.

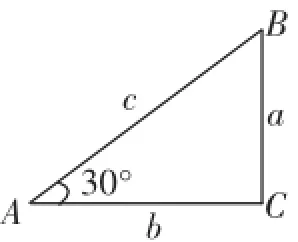
图6

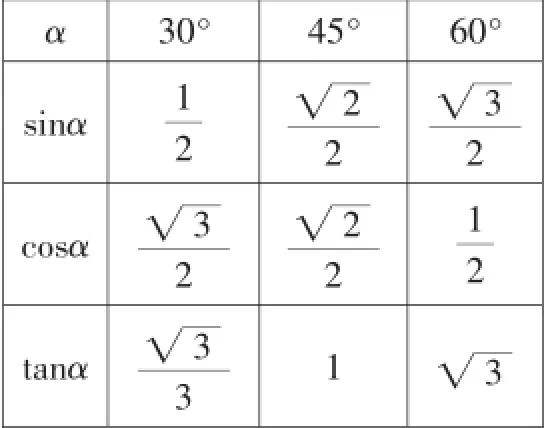
（2）交流研究60°的三角函数值的方法.

方法1：根据定义求得60°的三角函数值分别为：

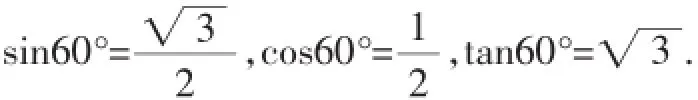
方法2：根据互余两角的三角函数的关系，直接求得60°的各三角函数值，并将结果填入上表.

（3）用同样方法求得45°的三角函数值后填入上表.

（四）引导学生观察30°、45°、60°的三角函数值表，探究表中数值间的内在关系

1.学生独立研究，伴以小组议论

2.全班交流

3.在学生交流的基础上，教师适时点拨归纳

（1）根据互余两角的三角函数关系式，只需记住30°、45°、60°的正弦、正切值就可知它们的余弦、余切值.

（2）发现：①锐角α的正弦、正切值是随角α的增大而增大的，而余弦值是随角α的增大而减小的；②0＜sinα＜ 1，0＜cosα＜1（α为锐角）；③角α的正弦与余弦的比等于角α的正切，

因此也可以根据同一个角的各三角函数的关系来记忆特殊角的三角函数值.

（3）请同学们思考同一个角的正弦和余弦之间有什么关系，能否根据定义证明sin2α+cos2α=1？

（五）师生共同总结

（1）锐角三角函数的实质是所在直角三角形的两边的比值，当一个角确定时，每一个比值也就唯一确定了.每一个比值都是这个角的一个函数，这个角是自变量.

（2）掌握了锐角三角函数的定义，特殊角的三角函数值、三角函数的增减性、互余两角的三角函数的关系式以及同角三角函数的关系式便迎刃而解了，因而掌握定义是关键.

二、课例赏析

1.从函数视角构思锐角三角函数的概念，思辨整体与个别的关系

锐角三角函数的实质是直角三角形中的锐角与两边之比的变化对应关系，知识的背景是函数的定义和“相似三角形对应边成比例”的性质.教材把“锐角三角函数”编排在“函数”和“相似三角形”的后面是符合知识的逻辑结构顺序的，因此应以函数的观点来审视本节教材，突出在Rt△ABC中，c为斜边，a、b为直角边，当锐角取一个确定的值值唯一确定，所以每一个比便是该锐角的一个函数，该锐角为自变量.根据知识的本质，应将这三个比的名称——锐角的正弦、余弦、正切同时给出，使学生整体认识且在整体中辨别，易于掌握概念.

2.从直角三角形中不同边之比出发展现全貌，让学生“心中有森林”

我们知道教材上是几个不同的锐角三角函数分开，逐一学习，这是一种“先见树木，再遇森林”的做法.我们认为可将学生置于“流动”知识链，首先让学生心中有全貌，然后让知识随学生思维的推动而延伸，让学生的思维随知识的必然发展而不断深化、活化.李老师的这节课以全屏的视野，为学生创设自主探究的背景，让学生沿着发展、对应、构建函数研究特性的线索，展开对三角函数最基本内容的全面探究，学生从中获得的不仅仅是有关三角函数的知识，也不仅仅是基本思维品质的优化，还包括研究问题的思想方法与策略，也包括学生人格、情感等领域的发展.不可否认，这节课学习了比较多的知识，但是由于李老师洞察了知识的背景、本质及其逻辑结构，（学生对含30°、45°、60°角的直角三角形的性质已充分掌握）遵循这一科学规律，引导学生步步深入，不断建构，形成体系，所以也就顺理成章，自然生成.

3.关于课堂自然生长性的一些思考

实践研究发现，知识的理解必须要有一定的心理基础.在学生学习新概念之前，头脑中一定有与之有关的准备知识，并且这些有关的知识结构是能够被调动起来的，与新概念之间能够形成联系.学生对于新知识的理解与吸收是一个信息或要素组织的过程，理解不是直线式的简单的积累，而是螺旋式发展的.同时，理解还需要认知结构的再重组.就本课而言，对于理解李老师为什么弃用课本导入，而从知识内部的自然生长点切入教学，笔者做出以下大胆揣测：首先学生学习锐角三角函数的概念之前，头脑中具备了一些与之相关的知识结构，如函数的概念、直角三角形的知识、勾股定理、线段比的意义、三角形的相似等，学生如果不理解函数概念中两个变量的对应关系，也就不可能解锐角三角函数的角与边的比的对应关系；其次，学生对以上的这些相关概念知识的认知是否到位，对于学生建构锐角三角函数的概念起着至关重要的作用.基于以上两点，本课整体建构的基础可谓万事俱备，如此引入更是水到渠成了.本课也正是巧妙地抓住了知识生长的自然特点顺势而为，不仅学生不会感到“负担”，还在知识间的微妙深邃的联系中享受到了思维创造的乐趣，学生的学力也就在这种日积月累中不断发展.可见，课堂自然生成需要外部资源的储备，需要关注知识之间的内部关联，更是数学学科内在特点决定了的.

1.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

2.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

3.刘东升.专家教师课堂MPCK的特点——李庾南老师执教“因式分解”课例研究［J］.中学数学月刊，2014（3）.