相邻三项线性递推关系数列通项的简便求法
⦿ 陕西省西安市第七十一中学 尚 萍
1 一个实例及解法
例1已知数列{an}满足a1=1,a2=2,且an+1=2an+3an-1(n≥2,n∈N+).求数列{an}的通项公式.
解法1:常规解法.
因为an+1=2an+3an-1(n≥2,n∈N+),所以an+1+an=3(an+an-1)(n≥2).
又因为a2+a1=3,所以{an+1+an}是以3为首项,3为公比的等比数列.
所以an+1+an=3×3n-1=3n,从而
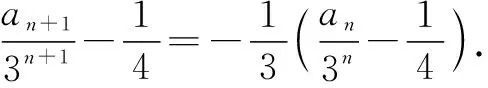
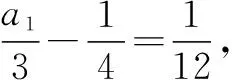
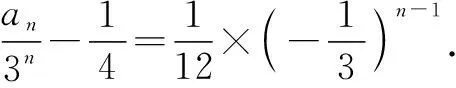
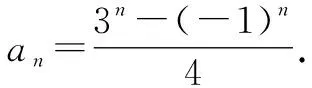
解法2:特征方程法.
设an+1-x1an=x2(an-x1an-1),与an+1=2an+3an-1比较系数,得
由韦达定理可知,x1,x2是方程x2-2x-3=0的两根-1和3.
取x1=-1,x2=3,有an+1+an=3(an+an-1).又因为a2+a1=3,所以{an+1+an}是以3为首项,3为公比的等比数列,所以an+1+an=3×3n-1=3n.
取x1=3,x2=-1,有an+1-3an=-(an-3an-1).又因为a2-3a1=-1,所以{an+1-3an}是以-1为首项,-1为公比的等比数列,则an+1-3an=(-1)×(-1)n-1=(-1)n.
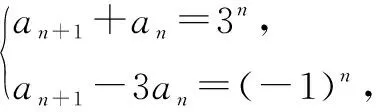
因此,设an=c1·(-1)n+c2·3n.
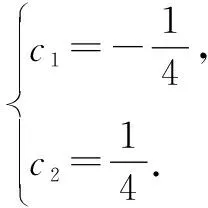
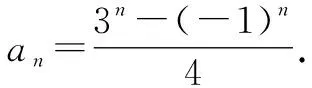
2 利用特征方程法解题的步骤
由例1解法2的解析可以看出,特征方程法是将相邻两项的线性组合构造成等比数列[1],而对应的系数刚好是题目中相邻三项线性递推关系数列的特征方程的根,通过解特征方程可以直接写出最终an的表达形式,再根据数列中的任意两项,求出线性组合的系数,最终得到数列{an}的通项公式[2].因此可以将解题过程简化为以下三个步骤:
(1)写出特征方程并求出两根x1,x2;

(3)将a1,a2的值代入求出系数c1,c2,进而写出数列{an}的通项公式.
例2已知数列{an}满足a1=a2=2,且an+1=3an+4an-1(n≥2,n∈N+).求数列{an}的通项公式.
解析:特征方程法.
由题可知,数列的特征方程为x2-3x-4=0,解方程得x1=4,x2=-1.
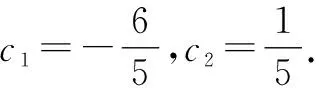

由例2的解析[3]可以看出,利用特征方程法解决此类问题具有简洁快速的明显优势,同时在解题过程中不容易出现错误,非常适合高中阶段的学生学习和理解.
3 特征方程法应用中的问题及对策
利用特征方程法求解这类问题,关键是构造特征方程.对于形如an+2=aan+1+ban(a,b为常数)的递推数列,它的特征方程是x2=ax+b,即x2-ax-b=0.
另外,既然是二次方程就可能存在两个相等的根和无实根的情形,下面对这两种情形进行探究.
例3已知数列{an}满足a1=1,a2=2,且an+1=6an-9an-1(n≥2,n∈N+).求数列{an}的通项公式.
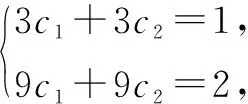
因此 ,例3无法用特征方程法快速求出通项公式.下面继续用构造等差数列的方法重新求解,探求新思路[2].
解析:常规解法.
因为an+1=6an-9an-1(n≥2,n∈N+),所以an+1-3an=3(an-3an-1)(n≥2).又因为a2-3a1=-1,所以{an+1-3an}是首项为-1,公比为3的等比数列.
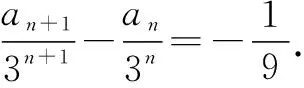
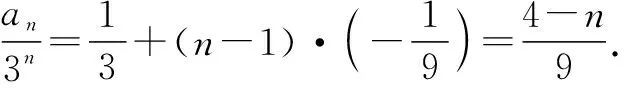
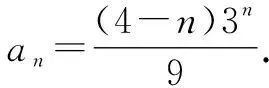
由例3可以看出,当特征方程有两个相等的根时,无法用特征方程法求出数列的通项公式,此时需要构造一个新的等差数列,求出这个等差数列的通项公式是An+B的形式,进而求出数列{an}的通项公式an=(An+B)·xn.
例4已知数列{an}满足a1=1,a2=2,且an+1=an-an-1(n≥2,n∈N+).求a2 024.
解析:由题可知,数列的特征方程为x2-x+1=0,此方程无实数根.
由a1=1,a2=2,an+1=an-an-1分别计算可得
a3=1,a4=-1,a5=-2,a6=-1,a7=1,a8=2,……
所以{an}是周期为6的周期数列,又
2 024÷6=337……2,
所以a2 024=a2=2.
由例4可以看出,当特征方程无实数根时,数列{an}是一个周期数列[2].这一结论具有普遍性,在这里省略证明.
4 特征方程法的解法总结
根据例2~例4的解答过程可以将相邻三项线性递推关系数列通项公式的求解归纳如下:
(Ⅰ)当特征方程有两个不相等的实根时
(1)写出特征方程并求出两根x1,x2;
(2)设an=c1·(x1)n+c2·(x2)n;
(3)将a1,a2的值代入,求出系数c1,c2,进而写出数列{an}的通项公式.
(Ⅱ)当特征方程有两个相等的实根时
(1)写出特征方程并求出根x;
(2)设an=(An+B)·xn;
(3)将a1,a2的值代入,求出系数A,B,进而写出数列{an}的通项公式.
(Ⅲ)当特征方程无实数根时
分别计算前几项的值,判断数列{an}的周期性,进而求出{an}的通项公式.

