用特征根法求数列通项公式
2022-02-25 02:51:10刘大鹏
数理化解题研究 2022年1期
刘大鹏
(辽宁省黑山县第一高级中学 121400)
本文用特征根法解决已知a1,a2,an+2=aan+1+ban,求数列通项公式型问题.
1 特征方程及特征根的定义
定义方程x2-ax-b=0叫做递推公式an+2=aan+1+ban的特征方程,其根叫做特征根.
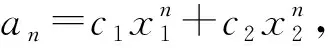
证明(用第二数学归纳法)
(1)当n=1时,a1=c1x1+c2x2结论成立.
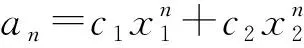
当n=k+1时,
ak+1=aak+bak-1
综上,结论对一切自然数n都成立.
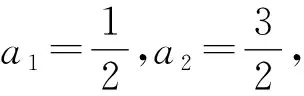
解析特征方程为x2-2x-3=0,
解得x1=-1,x2=3.
所以an=c1(-1)n+c23n.
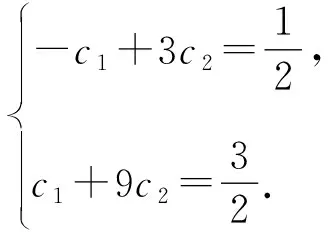
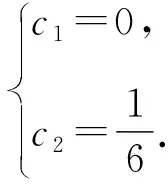
例2 (2006年福建文22)已知数列{an},a1=1,a2=3,an+2=3an+1-2an,n∈N*,求{an}的通项公式.
解析特征方程x2-3x+2=0的根为x1=1,x2=2.
所以an=c1+c22n.
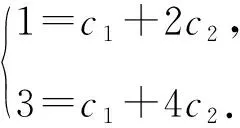
解得c1=-1,c2=1.
所以an=-1+2n.
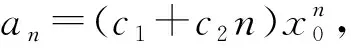
证明(1)当n=1时,a1=(c1+c2)x0结论成立.
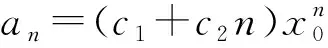
ak+1=aak+bak-1
综上,结论对一切自然数n都成立.
例3 (2008年天津文20)数列{an}中,a1=1,a2=2,an+1-an=q(an-an-1),(n≥2,q≠0),求{an}的通项公式.
解析特征方程x2-(q+1)x+q=0的根为x1=1,x2=q.
①当q=1时,an=(c1+c2n),
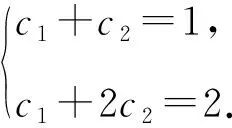
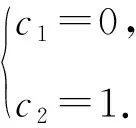
所以an=n.
②当q≠1时,an=c1+c2qn,
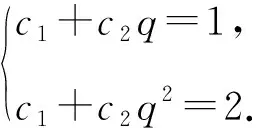
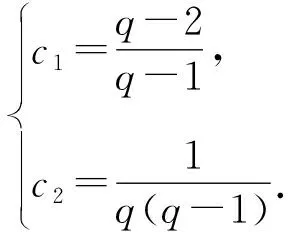
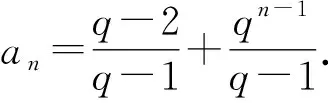
定理3 若特征方程有两个共轭虚根
x1=r(cosθ+isinθ),x2=r(cosθ-isinθ),
则an=rn(c1cosnθ+c2sinnθ),
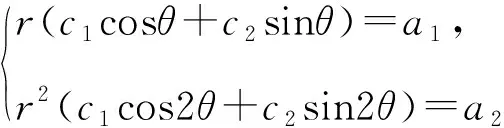
证明见文[2].
例4 (自编新题)已知数列{an},a1=1,a2=3,an+2=2an+1-4an,n∈N*,求{an}的通项公式.
解析特征方程x2-2x+4=0的根为
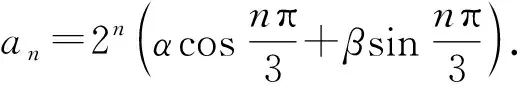
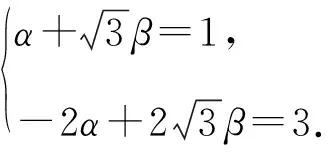
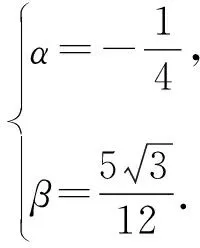
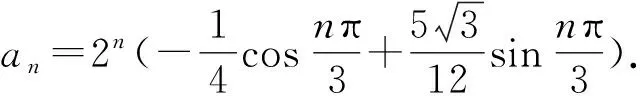
猜你喜欢
中学数学(2024年9期)2024-05-20 02:04:14
数理天地(高中版)(2022年19期)2022-05-30 10:48:04
新高考·高三数学(2022年3期)2022-04-28 08:41:42
数学大世界(2021年1期)2021-02-06 10:07:52
中学生数理化(高中版.高二数学)(2020年9期)2020-10-27 02:32:58
中学生数理化(高中版.高二数学)(2020年9期)2020-10-27 02:32:46
河北理科教学研究(2020年1期)2020-07-24 08:14:34
郑州大学学报(理学版)(2020年1期)2020-02-08 08:40:00
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27 20:09:58
Chinese Medical Sciences Journal(2019年1期)2019-04-11 09:26:46

