近五年全国卷Ⅰ物理选修3-5模块命题特点及教学启示

陈洪军

(江苏省镇江心湖高级中学 212132)

高中物理选修三系列教材中，3-5模块主要研究动量守恒、原子原子核及波粒二象性等内容，在全国高考中的考查经历了由2016年及之前的选考发展到今天的必考，而且有与其他物理规律综合交叉考查的发展趋势，彰显出国家层面对育理工人才、选拔科技人才的新的理念，因此，对高考试题中3-5模块试题的分析研究显得尤为必要，这里针对全国卷I近五年3-5部分的试题作一粗浅统计分析.

1 近五年全国卷Ⅰ 3-5模块内容考查统计

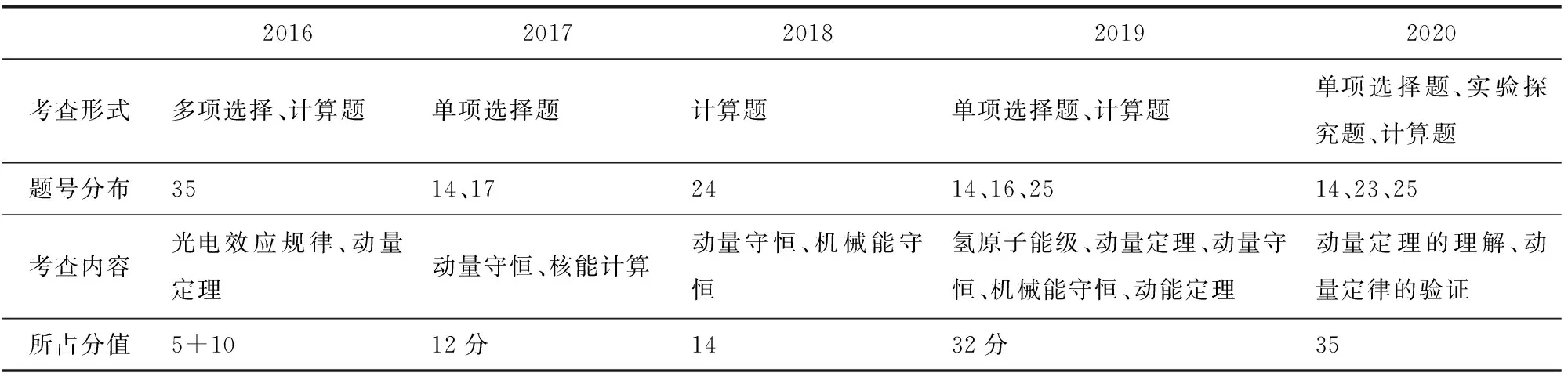
表1 近五年全国卷Ⅰ 3-5模块内容考查统计

由表中对近五年全国卷Ⅰ 3-5部分的考查统计不难发现以下规律：

(1)试题形式上看，3-5部分的考查囊括了填空、单项选择、多项选择及计算等几乎所有形式的物理题型，且近年来越来越趋向于以计算题形式呈现;

(2)题号上看，因2016及以前是选考题形式考查，2017及以后以必考题形式考查，故2016固定在第35题，而随后的2017、2018、2019、2020在试卷中呈现的次序则从14至25不等，题号灵活多样，不拘泥于35题一种题号;

(3)从试题数目上看，近五年呈现出由2016的固定为全卷第35一道题发展至2017年的两道题，再缩减至2018年的一道计算题，最后上升至2019和2020年的三道题，可谓一波三折，有增有减；

(4)从设问数目来看，计算题均为多个小问形式呈现，目的是增强考查面，使知识点尽可能多的覆盖到;

(5)从考查内容上看，以动量定理、动量守恒为高频考点，其余如光电效应、氢原子能级、核能等时有考查，且动量守恒的考查由过去的单独命题考查，发展至与机械能守恒、动能定理等必修系列内容的综合渗透考查；

(6)分值上看，3-5模块在高考中的分值占比由16年的15分降至17年的12分，再回升至2018年的14分，而2019年却高达32分之多，2020年最多为35分，显然，全国卷Ⅰ对3-5模块的考查变得越发重视，试题综合性程度变强、所涉物理定律、定理变多，所占分值也随之变大.

2 典型试题剖析

2.1 光电效应的考查

例1(2016全国卷Ⅰ)现用一光电管进行光电效应的实验，当用某一频率的光入射时，有光电流产生.下列说法正确的是____.

A．保持入射光的频率不变，入射光的光强变大，饱和光电流变大

B．入射光的频率变高，饱和光电流变大

C．入射光的频率变高，光电子的最大初动能变大

D．保持入射光的光强不变，不断减小入射光的频率，始终有光电流产生

E．遏止电压的大小与入射光的频率有关，与入射光的光强无关

命题意图本例以多项选择的形式考查学生对光电效应发生条件、光电子最大初动能和饱和光电流的影响因素及遏止电压等光电效应规律的理解.

试题解析答案：ACE

2.2 氢原子能级的考查

例2 (2019全国卷Ⅰ)氢原子能级示意图如图1所示.光子能量在1.63 eV～3.10 eV的光为可见光.要使处于基态(n=1)的氢原子被激发后可辐射出可见光光子，最少应给氢原子提供的能量为( ).

A．12.09 eV B．10.20 eV

C．1.89 eV D．1.5l eV

命题意图试题给出氢原子能级图及可见光光子能量范围，考查学生对原子跃迁条件、原子发光频率条件等玻尔假设的理解.

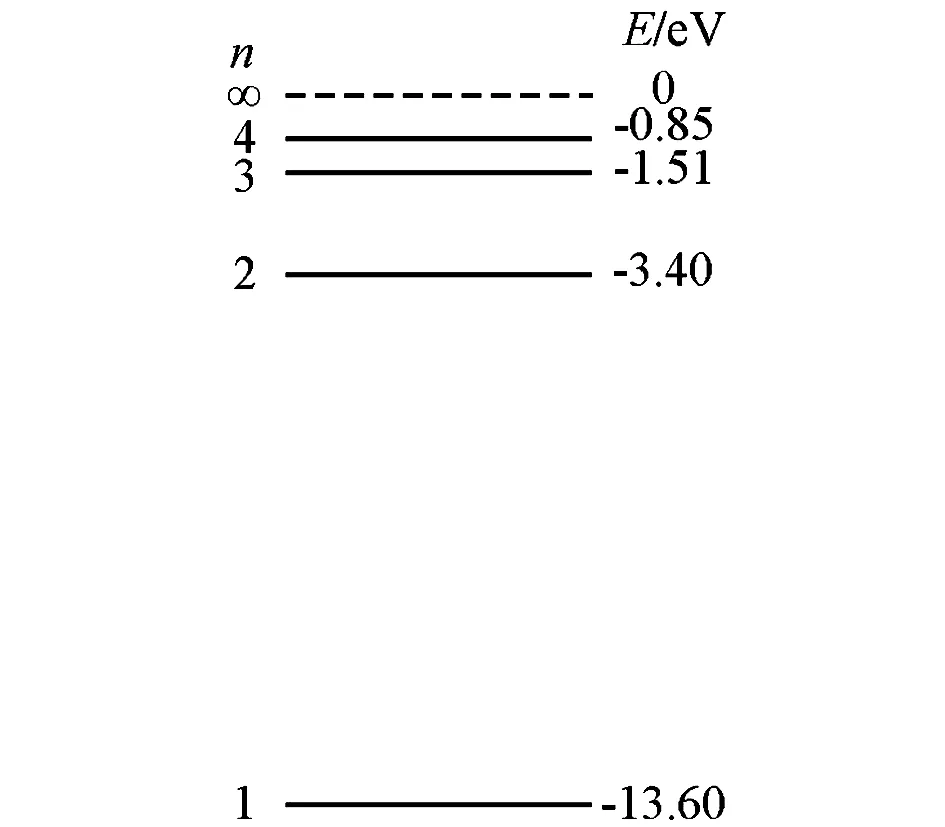
图1

试题解析处于基态的氢原子其能量为-13.6eV，当其跃迁到量子数为2的能量状态时，至少要向其提供-3.40eV-(-13.6eV)=12.09eV能量，而后其可向基态跃迁，辐射出可见光光子.

2.3 核能计算的考查

A．3.7MeV B．3.3MeV

C．2.7MeV D．0.93MeV

命题意图试题给出了核聚变的经典核反应方程式，要求学生计算所释放的核能，旨在考查学生运用质量亏损法计算核能的能力.

试题解析核能为△E=3.2585MeV≈3.3MeV,选项B正确.

2.4 动量定理的考查

例4(2016全国卷Ⅰ)某游乐园入口旁有一喷泉，喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中.为计算方便起见，假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出；玩具底部为平板(面积略大于S)；水柱冲击到玩具底板后，在竖直方向水的速度变为零，在水平方向朝四周均匀散开.忽略空气阻力.已知水的密度为ρ，重力加速度大小为g.求:(1)喷泉单位时间内喷出的水的质量；(2)玩具在空中悬停时，其底面相对于喷口的高度.

命题意图知识角度，试题考查动量定理、物体平衡、匀变速直线运动、牛顿运动定律等核心知识；能力角度，试题以生活中常见的喷泉为命题背景，考查了学生将具体情境转化为物理问题的模型构建能力、运用核心定律综合分析推理能力及解决实际问题的能力；核心素养角度，通过对学生的模型建构、演绎推理科学思维素养的考查，旨在对学生通过学习是否形成了正确的相互作用观、运动观、物质观和能量观等物理观念.

试题解析(1)设极短时间Δt内喷出的水柱高度为Δh，因所取时间极短，故可看成以速度v0匀速运动，则有：

Δh=v0Δt

①

由密度公式得所形成水柱质量为：

Δm=ρΔV=ρsΔh

②

由①②两式可得在极短时间内Δt所形成的水柱质量为：

Δm=ρsv0Δt

③

将③式变形整理可得单位时间内喷泉喷出的水的质量为

(2)当玩具稳定在水柱上方时，由二力平衡得水柱对玩具的作用力：

F=Mg

由牛顿第三定律可得玩具对水柱的反作用力为：

F′=F=Mg

④

设在极短时间Δt内水柱到达玩具底部时的速度为v1，竖直方向由动量定理可得：

(F′+Δmg)·Δt=Δmv1

⑤

再由匀变速直线运动规律得：

⑥

因极短时间内水柱质量Δm很小，⑤式左边可将其忽略为零，则由③、④、⑤三式可得高度

2.5 动量守恒与机械能的渗透考查

例5(2018全国卷Ⅰ改编)一质量为m的烟花弹获得动能E后，从地面竖直升空，当烟花弹上升的速度为零时，弹中火药爆炸将烟花弹炸为质量相等的两部分，两部分获得的动能之和也为E，且均沿竖直方向运动.爆炸时间极短，重力加速度大小为g，不计空气阻力和火药的质量，求爆炸后烟花弹向上运动的部分距地面的最大高度.

命题意图试题以学生熟悉的烟花弹的燃爆为背景，将守恒思想(动量守恒、能量守恒)植入其中，考查学生在具体生活情境中运用守恒思想解决实际问题的能力.

试题解析烟花弹自地面升至高为H1过程中根据机械能守恒定律得

mgH1+0=E+0

①

因烟花弹被炸成一上一下两部分则爆炸前后由动量守恒得

m1v1+m2v2=0

②

又据爆炸前后两部分动能之后仍为E得

③

由题意知被炸后的两部分质量相等，均为均为

④

爆炸后的上部分自爆炸后瞬间至最高点由机械能守恒定律得

⑤

综合①②③④⑤式可得，爆炸后烟花弹上部分距地面的最大高度为