一些常系数非齐次线性微分方程的复数解法
成都信息工程学院数学学院 杜先云
绵阳师范学院数学与物理学院 任秋道
一、引入
现行《高等数学》中微分方程给出了二阶常系数非齐次线性微分方程
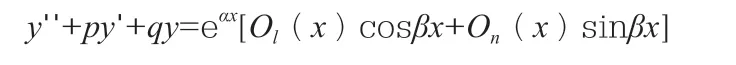
的解法,解的形式需要求待定多项式,过程较复杂。我们给出该类型微分方程的复数解法,方法简单,还可以减少计算量。
二阶常系数非齐次线性微分方程y''+py'+qy=Pm(x)eλx(λ∈C)的特解为
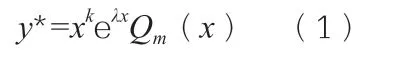
其中,Qm(x)是与Pm(x)同次(m次)多项式,而k要分三种情况:当λ不是特征方程的根、是特征方程的单根及是特征方程的二重根时,k分别取0、1 及2。
二、复数的解法
讨论下列二阶常系数非齐次线性微分方程:
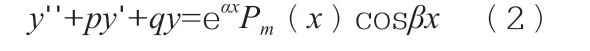
或
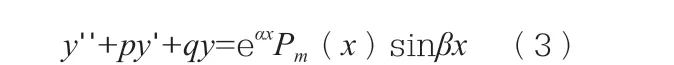
或
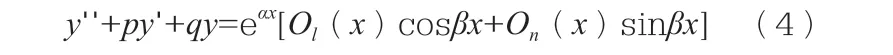
的解,其中,p,q,α,β∈R,Ol(x),On(x)及Pm(x)分别为l,n及m次实系数多项式。
定理:方程(2)与(3)的解分别是复数方程y''+py'+qy=Pm(x)eλx的解的实部和虚部,它们的特解分别是
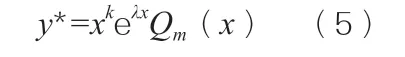
的实部和虚部,特解的共同形式:

其中,Qm(x)是m次复系数多项式,且当λ=α+βi不是特征方程的根与是特征方程的根时,k分别取0 及1。


方程(2)的解y1*=Rey=xkeαx[Qu(x)cosβx-Qv(x)sinβx],方程(3)的解y2*=Imy=xkeαx[Qu(x)sinβx+Qv(x)cosβx],它们有共通形式:y=xkeαx[cosβxRm(x)+sinβxSm(x)]。
推论:方程(4)的特解为y*=Re[xkeλxQl(x)xk]+Im[xkeλxQn(x)]=xkeαx[cosβxRm(x)+sinβxSm(x)],其中,Ql(x)与Qn(x)分别是l与n次复系数多项式,Rm(x)与Sm(x)是m(m=max{l,n})次实系数多项式,当λ=α+βi不是特征方程的根与是特征方程的单根时,k分别取0 及1。


其中,Rm(x)与Sm(x)是m(m=max{l,n})次实系数多项式,而当λ=α+βi不是特征方程的根与是特征方程的根时,k分别取0 及1。

