高中数学探究活动课“圆的切线与切点弦”教学设计

编者按：课堂是教学的主阵地。优秀的教学设计能为教师提供经验与启示，帮助教师提高教学质量。为此，2024年，本刊开设专栏《典型课例》。在该栏目中，我们以“教学设计+点评”的形式，呈现一线教师学习、理解新课标，深化素养导向的课堂教学改革和育人方式转变的实践与思考。我们主要呈现2023年江苏省优质课评比一等奖的教学设计，希望通过这些典型课例，引领教师关注教学细节，激发教学灵感，在实践中探索、总结和创新，不断提升教学质量。

【关键词】高中数学；数学探究；教学设计；圆的切线与切点弦

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2024）03-0043-04

【作者简介】刘银，江苏省镇江第一中学（江苏镇江，212016）教师，数学学科中心教研组长，高级教师，镇江市数学学科带头人。

一、教学内容分析

《普通高中数学课程标准（2017年版2020年修订）》（以下简称“新课标”）指出：数学探究活动是围绕某个具体的数学问题，开展自主探究、合作研究并最终解决问题的过程。［1］这种活动是运用数学知识解决数学问题的综合实践活动，是培养学生创新意识和能力的重要途径。

本节课的内容选自苏教版《普通高中教科书·数学》（选择性必修第一册）第2章《圆与方程》章末“问题与探究”，是本章知识的延伸和拓展，也是后续圆锥曲线相关内容学习的起点和基础。本节课旨在引导学生运用数形结合、转化化归等多种思想方法，深化学生对“代数方法解决几何问题”的理解和认识。本节课是通过研究点与直线的“对应组”和圆之间的位置关系，让学生深入体会点在圆上、点在圆外、点在圆内三种情况及三者之间相互递推的逻辑关联。在类比联想、分类整合等过程中，让学生体会数学的简洁、统一、和谐、理性之美。

二、教学目标设置

1.经历直观想象、画图试验、观察类比、猜想验证等探究过程，掌握过圆上一点的圆的切线方程的证明方法。

2.体会探究解析几何问题的基本方法，发现点不在圆上时方程“x0x + y0y = r2”的几何意义。

3.在发现问题、提出问题、分析问题、解决问题、再发现新问题的螺旋式上升的探究过程中，激发学生数学探究的兴趣与意识，积累活动经验，培育创新精神。

三、学情分析

1.学生已有的认知基础

本节课的授课对象是江苏省四星级高中高二学生，他们能从代数角度研究点、直线、圆之间的关系，初步具备研究解析几何的直接经验，具有一定的图形识别、问题发现以及探究推理能力。

2.达成目标所需的认知基础

圆的切线与切点弦中，点、线、圆的关系复杂且深刻，数形转化与融合程度要求较高，需要学生有良好的直观想象、逻辑推理能力和独立思考、合作交流等学习习惯。

四、教学过程设计

1.单元回顾，升华认识

师：数学用“符号”将世界抽象为形与数。前面我们学习了“圆与方程”，其中圆是“形”，方程是“数”。

【问题1】在《圆与方程》这一章我们研究过哪些知识？

【设计意图】通过问题，教师引导学生自主回顾单元知识，这一章主要研究了圆的代数表示以及点、线、圆的位置关系，引领学生进一步升华认识：单个图形主要研究它的方程及自身的结构特征；组合图形主要研究它们的位置关系。这为后续研究圆的切线与切点弦及获得探究路径作铺垫。

2.温故知新，方法引领

【问题2】已知点P（x0，y0）是圆O：x2 + y2 = r2上一点，请画出过点P的圆O的切线，并求切线方程。

学生活动：由于直线与圆相切，且P为切点，觀察到切线与OP垂直，先求直线OP的斜率，再根据斜率乘积为-1，得切线斜率，进而利用点斜式表示直线，但要单独考虑斜率不存在或者为0的情形；同样通过垂直，设切线上任意一点Q（x，y），借助向量，有[OP]·[OQ] = r 2，整理得解；观察到圆心到切线的距离等于半径，设直线方程，利用点到直线距离公式求解；观察切线与圆有唯一公共点，联立方程，根据方程根的判别式求解。

【设计意图】问题2是教材习题原题，求解方法较多，有代数、几何、向量三个视角，但总体来看都是在“形”上抓“垂直”。通过本题的探究，教师带领学生回顾求解方法和图形观察角度，助推学生总结直线与点、直线与圆位置关系的判断方法，引领后续探究。

【问题2.1】对于向量数量积与方程x0x0 + y0y0 = r2的结构上的联系，你还有新发现吗？

【问题2.2】从“数”的角度看，点、线、圆三者之间又有什么联系？

从“形”的角度看，P点在圆上，从“数”的角度方程上有x02 + y02 = r2，则点的坐标（x0，y0）满足方程x0x + y0y = r2。学生猜想：此直线是切线；事实上，可以进一步验证d = [r2x20+y20] = r，因此方程确实表示圆的切线。由此得到命题1。

命题1：当点P（x0，y0）在圆O：x2 + y2 = r2上时，方程x0x + y0y = r2表示圆的切线。

【设计意图】从数到形，以形助数，帮助学生获得方程背后的几何意义。上述探究过程紧扣教材，并将数学思想方法在课堂中落实。在分析解决问题的过程中，为后面“点不在圆上”情况的探究作铺垫，积累探究经验。

3.合作探究，形成路径

【问题3】数学家波利亚曾说：“解题就像采蘑菇，当我们发现一个蘑菇时，它的周围可能还有其他蘑菇。”你还想探究什么问题呢？

【设计意图】从点在圆上到点不在圆上，即从点的坐标满足圆的方程，到点的坐标不满足圆的方程，进而探究点在圆外和点在圆内。这里从相等到不等，从特殊到一般，引出课题，同时渗透了数学思想方法和数学文化。

【问题3.1】当点P（x0，y0）在圆外时，方程x0x+y0y=r2表示怎样的直线？

【问题3.2】你能在练习纸上画出这条直线吗？

【问题3.3】如图1，你能判断直线x0x + y0y = r2与点P（x0，y0），与圆x2 + y2 = r2的位置关系吗？如何判断？

【设计意图】通过问题链的方式，教师引导学生根据“点在圆上”的探究方法，交流、讨论，通过合作探究解决新问题。

教师补充定义：切点弦是一条特殊的弦，是过圆外一点引圆的两条切线连接两切点得到的。

学生活动：

（代数法）记直线与圆交于A，B两点，与OP交于点H，连接OA，OB，PA，PB。首先由直线斜率可判断OP与AB垂直，其次计算圆心到直线距离d=[r2x20+y20]，其中OP=[x20+y20]，所以OH·OP=r2，即OH·OP=OA2，所以△OAH ∽△OPA，则OA⊥PA。OA是半径，所以PA是切线，同理，PB是切线，方程x0x+y0y=r2表示切点弦。正向证明，由数想形，方程表示两切点所在直线。

（几何法）过点P作圆的切线PA，PB，则PA⊥OA，PB⊥OB，借助几何关系，有O，A，P，B在以OP为直径的圆上。该圆方程为x2 + y2 - x0x - y0y=0，AB为两圆相交弦，将两圆作差即可。这里的公共弦就是切点弦，与该直线方程x0x + y0y = r2一致。

（向量法）过点P作圆的切线PA，PB，记OP与AB的交点为H，设直线AB上任意一点，则通过向量知识有[OP]·[OQ] = OH·OP，此时OH·OP = r2，所以[OP]·[OQ] = r 2，即得直线方程x0x+y0y = r2。

【问题3.4】利用刚刚所得的“切线结论”（命题1），能推导出切点弦所在的直线方程吗？

学生活动：设A（x1，y1），B（x2，y2），切线PA的方程为x1x + y1y = r2，切线PB的方程为x2x + y2y = r2。它们均过点P，有x1x0 + y1y0 = r2，x2x0 + y2y0 = r2。x1x0 + y1y0 = r2与x2x0 + y2y0 = r2结构相同，两点确定一直线，即x0x + y0y = r2就是直线AB的方程。设而不求，将点在圆外化归到点在圆上，体现了转化与化归思想。由此得到命题2。

命题2：当点P（x0，y0）在圆O： x2+y2=r2外时，方程x0x+y0y=r2表示圆的切点弦所在的直线。

【设计意图】上述教学从数出发，探究方程背后所蕴含的几何特征，由数想形，以形助数。与“圆的切线”情形一致，仍在形上抓“垂直”，在数上看“结构”，代数、几何、向量三种视角前后贯通。在猜想与求证中，学生判断出直线不经过该点、直线与圆相交，逐步精准定位，得出方程x0x + y0y = r2表示切点弦所在的直线。

4.自主探究，形成体系

【问题4】当点P（x0，y0）在圆内时（P异于O），方程x0x + y0y = r2表示怎样的直线？

学生活动：过P点作直线，与圆O交于A，B两点，分别过A，B两点作圆O的切线，设两切线的交点Q（m，n），则直线AB可表示为xm+yn=r2。点P在AB上，则x0m+y0n=r2，所以Q点的轨迹方程为x0x+y0y=r2。这个过程就是刚刚“切点弦”逆过来，体现了化归思想。由此得到命题3。

命题3：当点P（x0，y0）在圆O： x2+y2=r2内时，方程x0x+y0y=r2表示圆的弦切线交点的轨迹。

【设计意图】“点在圆上”师生共研，感悟探究方法；“点在圆外”生生合作，形成探究路径；“点在圆内”充分发挥学生的主观能动性，教师从引导者转变为“旁观者”、合作者，帮助学生从“学会”到“会学”。

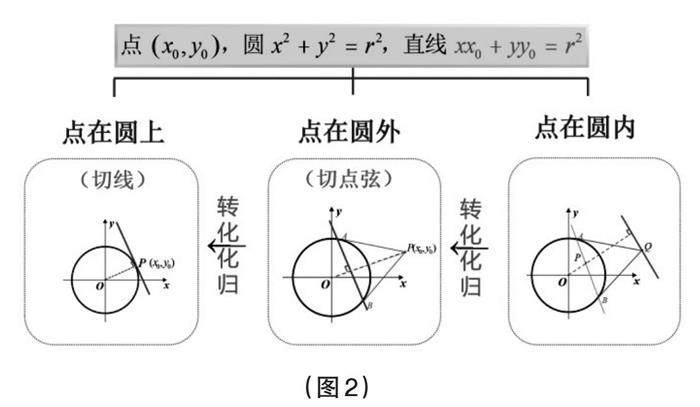
【问题4.1】点在圆上、点在圆外、点在圆内，它们之间有怎样的联系？

教师借助GeoGebra软件动态演示，让学生从几何直观和理性层面体会三种情况下的变与不变。（如图2）三个问题彼此关联（直线始终与OP垂直），又层层递进。过程中，学生感悟到转化与化归的数学思想，即“点在圆外”可以转化到“点在圆上”求解，而“点在圆内”又可以转化到“点在圆外”求解。教学中，教师还借用了笛卡尔的名言：“我解决过的每一个问题都成为日后用以解决其他问题的法则。”渗透了数学文化。

5.总结回顾，探究继续

【问题5】请同学们从知识、方法、思想几方面回顾本节课的收获。

学生活动：学生结合板书分别从知识、方法、思想等层面总结。知识层面上，点P（x0，y0）在圆O： x2 + y2 = r2上时，直线x0x+y0y=r2表示圆的切线；点P（x0，y0）在圆O： x2 + y2 = r2外时，直线x0x +y0y = r2表示圆的切点弦所在直线；点P（x0，y0）在圆O： x2 + y2 = r2内时直线x0x + y0y = r2表示圆的弦切线交点的轨迹。探究方法上，有类比、联想、实验、猜想等。在数学思想上，學生体会了数形结合、特殊到一般、转化与化归。探究中借助了代数、几何、向量三个视角，其中学生特别体会了代数法在解析几何中的应用魅力。

【设计意图】引导学生学会寻找研究方法、付诸实践，学会反思学习过程，提炼研究成果。

6.课后作业，深化巩固

【思考运用】当“圆心不在原点”时，如何研究圆的切线与切点弦？

【探究拓展】运用今天的研究方法，你还能进行其他探究吗？

【设计意图】满足不同层次学生的需求，将探究意识从课内延伸到课外，激发学生后续的研究兴趣，为学生构建“前后一致、逻辑连贯”的学习过程。

【参考文献】

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020：35.

［2］单墫，李善良.普通高中数学教科书·数学（选择性必修第一册）［M］.南京：江苏凤凰教育出版社，2021：72.