数学建模核心素养视域下的高考试题评析

邓雯静

摘 要：2023年全国新高考数学Ⅰ卷从多个角度对学生的思维能力、创新能力等方面进行考查，凸显数学建模核心素养.通过对2023年全国新高考数学Ⅰ卷的评析，体会如何在教学中渗透数学建模核心素养，给高中数学的教学提供一些启示.

关键词：数学建模；新高考；核心素养

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0079-03

《普通高中数学课程标准（2017年版2020年修订）》中指出：数学建模作为数学学科六大核心素养之一，要求学生能够在实际情境中运用所学习的知识抽象出数学问题，结合逻辑推理、直观想象的能力建立数学模型，并计算求解，最终解决实际问题［1］.2023年全国新高考数学Ⅰ卷充分体现了新课标对数学学科核心素养的要求，从多个角度对数学建模核心素养进行考查，下面以试题为例进行剖析.

1  数学模型在现实情境中的构建

2023年全国新高考数学Ⅰ卷部分试题背景素材紧密联系社会生活实际.例如，人们越来越重视噪声污染，高考试题便在这个方面有所体现，第10题以燃油汽车、混合动力汽车、电动汽车三种声源产生的声压为背景材料，将实际问题抽象为构建有关声压的数学模型，让学生初步体会运用数学模型解决实际问题.

1.1 现实情境下的函数模型

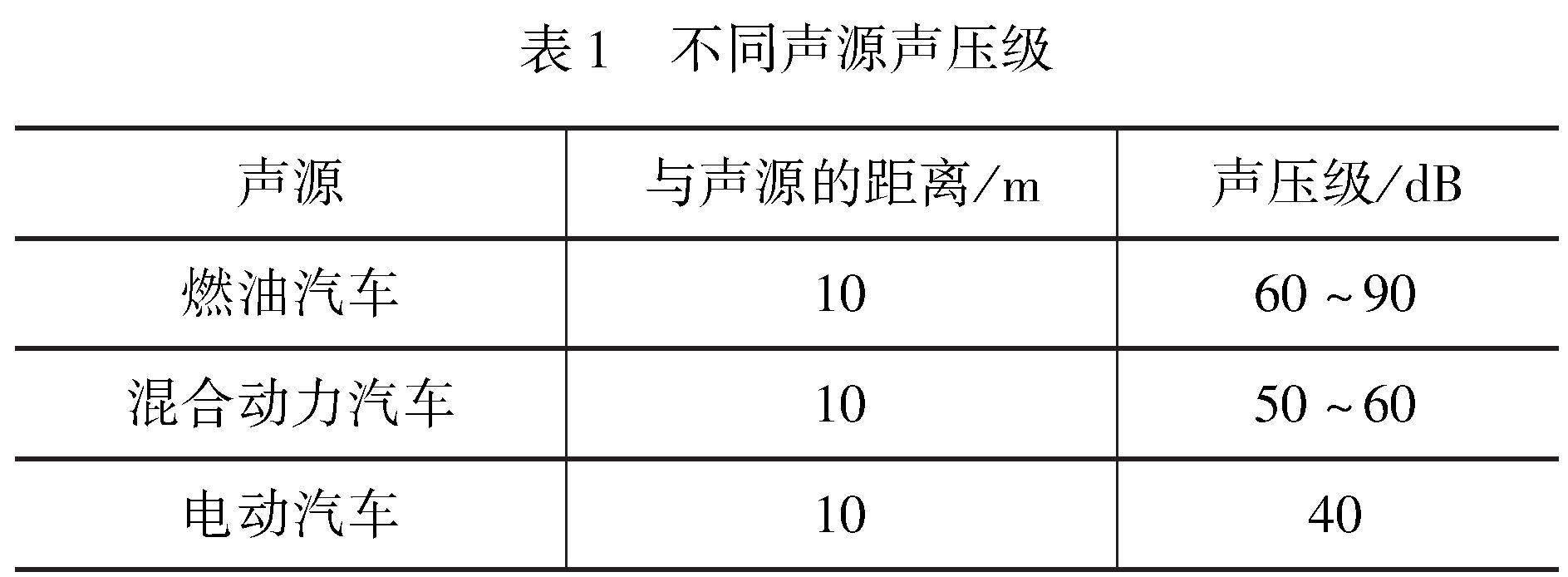
例1 （2023年全国新高考数学Ⅰ卷第10题）噪声污染问题越来越受到重视，用声压级来度量声音的强弱，定义声压级Lp=20×lgpp0，其中常数p0（p0>0）是听觉下限阈值，p是实际声压，不同声源的声压级见表1：

已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为p1，p2，p3，则（  ）.

A. p1≥p2   B.p2>10p3

C. p3=100p0D.p1≤100p2

分析 本题是在一个社会问题背景下，将声压级数学模型通过函数解析式给出，需要学生在阅读理解下抓取关键信息，梳理清楚各数据之间的关系，结合选项合理运用条件中的数学模型探究p1，p2，p3之间的关系，并利用对数运算性质展开计算［2］.

解法1 根据题意可知Lp1∈［60，90］，Lp2∈［50，60］，Lp3=40.

选项A：将对应函数值相减可得

解法2 根据题意可得

即p2≤1 000p0≤p1，故A正确.

故选ACD.

1.2 现实情境下的概率模型

例2 （2023年全国新高考数学Ⅰ卷第21题）甲、乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮.无论之前投篮情况如何，甲每次投篮的命中率均为0.6，乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选，第1次投篮的人是甲、乙的概率各为0.5.

（1）求第2次投篮的人是乙的概率；

（2）求第i次投篮的人是甲的概率；

分析 本题从投篮实例出发，从题干中分析出概率模型进行求解，需要学生理解条件概率与全概率公式模型之间的关系以及两点分布模型的特点，在递推的过程中使用数列模型求解，不仅体现了数学建模核心素养，还考查了学生的数学运算能力.

解析 （1）记“第i次投篮的人是甲”为事件Ai，“第i次投篮的人是乙”为事件Bi，所以

P（B2）=P（A1B2）+P（B1B2）

=P（A1）P（B2|A1）+P（B1）P（B2|B1）

=0.5×（1-0.6）+0.5×0.8=0.6.

（2）设P（Ai）=pi，依题可知P（Bi）=1-pi，

则P（Ai+1）=P（AiAi+1）+P（BiAi+1）

=P（Ai）P（Ai+1|Ai）+P（Bi）P（Ai+1|Bi）.

即pi+1=0.6pi+（1-0.8）×（1-pi）

=0.4pi+0.2.

构造等比数列 {pi+λ}，

（3）设第i次投篮时甲投篮次数为Xi，且Xi的可能取值为0或1，Xi服從两点分布，则P（Xi=1）=pi，P（Xi=0）=1-pi，E（Xi）=pi.

前n次中甲投篮的次数

Y=X1+X2+X3+…+Xn，

则 E（Y）=E（X1+X2+X3+…+Xn）

=p1+p2+p3+…+pn.

2 几何、代数模型在数学情境中的整合

2023年全国新高考数学Ⅰ卷第16题是在双曲线、向量、余弦定理公式模型下进行探究求解，更体现了数学模型综合性的运用.

分析 根据双曲线的概念性质、向量运算以及几何意义得到|AF2|，|BF2|，|BF1|，|AF1|关于a，m的表达式，利用勾股定理求得a=m，通过余弦定理得到a，c的齐次方程，从而求得双曲线离心率.也可依题意设出各点坐标，利用向量坐标运算求解点A坐标，将点A代入双曲线C 得到关于a，b，c的齐次方程，求得离心率.

在Rt△ABF1中，9m2+（2a+2m）2=25m2，

即a=m或a=-3m（舍去）.

整理，得5c2=9a2.

3 结束语

在新课标的背景下，培养学生的数学建模核心素养成为教学的重点，传统课堂已经满足不了教学的需要，因此高中数学教师必须转变教学方式，在课堂中逐渐渗透数学建模素养.在教学中无论是探究初等基本函数，还是向量、立体几何、圆锥曲线等，都通过构建数学模型，引导学生探究其性质特点，再进一步在实际问题中加以运用.在探究过程中，可以运用信息技术手段如几何画板GeoGebra等，引导学生小组合作绘制图象，构建模型，充分发挥学生的主观能动性，让学生在整个分析、构建、计算、检验、改进、解决的过程中，体会数学建模的应用价值.

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

［2］ 许正川.高中数学建模中问题的作用及发挥机制[J].数学教学通讯，2023（09）：38-39.