空间直线问题中的一题多解

王利波 徐瑰瑰

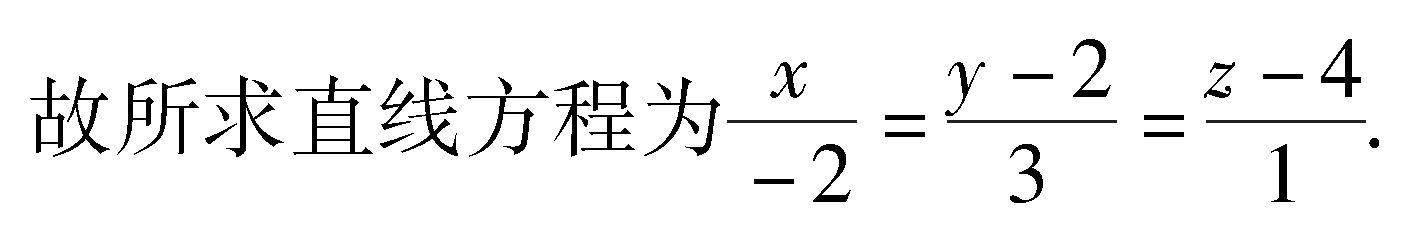
摘 要：文章从实例出发，讨论了空间解析几何的直线问题中的一题多解，有利于加强学生对基本概念的理解，有助于培养学生的发散性思维和创新能力.

关键词：直线；平面；方向向量；法向量；方程

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0072-04

直线是特殊的曲线，是空间解析几何中的基本图形. 空间直线方程常见表示形式有一般式方程、点向式（对称式）方程、参数方程、截距式方程等，由于其形式多样，于是求解直线方程的题目就可以从不同角度出发.本文主要介绍了空间直线问题中常见的四类综合题型，从多角度多侧面分析问题，借助向量的数量积、向量积、混合积和直线方程的表示方法，进而得到不同的解题方法.

1 与两平面平行的直线

例1 求过点（0，2，4）且与两平面x+2z=1和y-3z=2平行的直线方程.

解法1 （向量积）所给平面的法向量分别为n1=（1，0，2），n2=（0，1，-3），由于所求直线平行于两平面，则所求直线的方向向量s垂直于所给平面的法向量，即s⊥n1且s⊥n2，于是可取所求直线的方向向量

s=n1×n2=-2i+3j+k［1］.

解法3 （平行平面）

过点（0，2，4）且与平面x+2z=1平行的平面方程为x+2z=8，过点（0，2，4）且与平面y-3z=2平行的平面方程为y-3z=-10［2］.

2 与已知直线垂直相交的直线

解法1 （向量积）由于点B（2，-2，3）在已知

设所求直线的方向向量为s1，则由题意可知

s1⊥s且s1⊥n，故所求直线的方向向量为

s1=s×n=-5i+7j-2k.

即m+n+p=0.①

又由于所求直线与已知直线垂直，则s1⊥s，于是s1·s=0，即3m+n-4p=0.②

则（5，-7，2）可作为所求直线的方向向量.

3 直线在已知平面上的投影直线

解法2 （混合积）设所求直线的方向向量s=（m，n，p），则s=（m，n，p）垂直于所给平面x+y+z=0的法向量n=（1，1，1），

即m+n+p=0.④

即n-p=0.⑤

联立④和⑤可得m=-2p，n=p，所以所求直线的方向向量可取为（-2，1，1）.

解法4 （平面束方程）过已知直线的平面束方程为

x+y-z-1+λ（x-y+z+1）=0.

即（λ+1）x+（1-λ）y+（λ-1）z+λ-1=0.

该平面与已知平面垂直的充要条件是

（λ+1）·1+（1-λ）·1+（λ-1）·1=0，

解得λ=-1.

于是投影平面方程为y-z-1=0.

4 平行于已知平面且与已知直线相交的直线

解法1 （两点式方程）设所求直线与已知直线的交点坐标为（-1+t，3+t，2t），则以（-1，0，4）为起点，以（-1+t，3+t，2t）为终点的向量（t，3+t，2t-4）垂直于所给平面的法向量（3，-4，1），则

3t-4（3+t）+2t-4=0，

解得t=16.

解法2 （混合积）设所求直线的方向向量s=（m，n，p），则由题意可知s=（m，n，p）垂直于所给平面的法向量（3，-4，1），则

3m-4n+p=0.⑥

即10m-4n-3p=0.⑦

解法3 （向量積）

过点（-1，0，4）且平行于平面3x-4y+z-10=0的平面方程为

3x-4y+z-1=0，

5 结束语

本文例题虽然解法较多，但是万变不离其宗，文中都是从基础知识出发，运用了直线的两种表示方法.一是点向式方程，这就需要求出直线上一点以及直线的方向向量.通过上面的例题，不难发现，利用点向式表示直线方程的关键就是求解直线的方向向量，其求解方法不唯一，但是都是我们教材中讲过的数量积、向量积和混合积.所以，在解题过程中，要灵活运用所学知识去求解直线的方向向量.二是一般式方程，这就需要找出直线所在的两个平面及其方程.求解平面方程的关键是寻找平面的法向量，用到的知识依然是向量的数量积、向量积和混合积.

在教学活动中，引入一题多解，不仅可以引导学生从多角度去思考问题，而且可以提高学生的学习兴趣，还可以帮助学生学会知识的迁移并灵活运用所学知识去解决问题，进而举一反三、融会贯通.

参考文献：

［1］陈淑贞.空间直线方程的解题探讨[J].海南师范大学学报（自然科学版），2011，24（3）：348-351.

[2] 王亚南，寇光兴.空间直线方程问题的一题多解[J].高等数学研究，2021，24（2）：27-30.